The system, named after the French mathematician, is very simple in principle. You bet on a suit (preferably always the same suit, but it doesn't really matter), with the bet increasing by 1 chip if you lose, and decreasing by 1 chip if you win.
What about statistics?
If we assume that the ratio of the two suits is roughly the same on average over the long term, so the number of wins and losses should be similar, then in principle all wins should be a chip higher than losses, so we earn a chip on each win-loss pair (we can safely ignore the zero in the calculation, as it will affect the win-loss ratio only slightly compared to the number of chips we win). This looks very clever and promising. So let's see what it will actually look like.
Lo and behold, the whole graph goes quite clearly into the negative, and quite significantly. At 25,000 spins, the resulting loss appears to be around 300,000 chips. The course of the whole system does not change even when testing hundreds of thousands of spins, which shows the very significant loss of the whole strategy.
What could be the error?
If we think about it carefully, we find that the whole system has one major flaw. While the wins and losses are balanced over the long term, they need to be in the right order. If the losses come first and then the wins, that is fine, but if we win first and then the losses come, the consequences are disastrous. Let's take an extreme example. Let's say we keep betting on red and it happens that first black hits 100 times in a row and then red hits 100 times in a row. On average, both colors fall equally often, so everything is fine. At first, we went into the red with 100 losses (about 100*50 = 5,000 chips minus), but then we made up for it with wins that were always a chip higher - so 100*51 = 5,100 chips plus, and after 200 spins we have a net profit of 100 chips, which is great.
However, if we hit first 100x red and then 100x black (again, on average, fine), the situation is completely different. First, we win one chip at a time - 100*1 = 100 chip gain, but then black comes and we take a loss of 100*50 = 5,000 chips, so the total is suddenly minus 4,900 chips for 200 spins, which is a bummer. It won't be that extreme in real life, but this effect is enough to send the whole system into a deep negative.
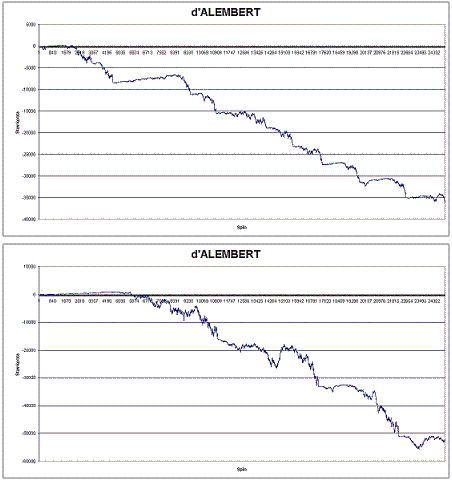
So, in the end, this system is already very bad in principle. We can try some more modifications, but we probably shouldn't get our hopes up. We'll see. For example, let's try to dampen the fluctuations with an upper bet limit, let's say a maximum bet of 100 and 200 chips, after which the bet resets back to 1 chip:
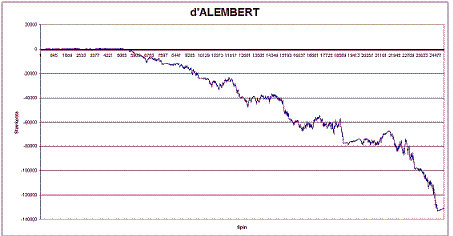
So no, no surprises. The course is exactly the same, only the resulting loss after 25,000 spins has been reduced from an average of 300,000 to some 40,000 chips, but that doesn't really lift our spirits... We can still try serial progression, where after each losing streak (or reaching the stake limit) we increase the base stake and further stake growth by one more chip compared to the previous streak until we are in the black. What happens?
Nothing, it's back to business as usual. Not even the aggressive martingale series progression (the next base stake and the next stakes in the series are not 1 chip higher, but are double the starting stake in the previous series) or the Fibonacci progression (the next starting stake is the sum of the previous two starting stakes) helps.
We can only conclude that this system is completely useless.
Moreover, we have prepared a roulette betting simulator, where you can try this system for free.

 EN
EN  čeština
čeština  Polski
Polski  Slovenčina
Slovenčina  Русский
Русский  Deutsch
Deutsch  Slovenski
Slovenski  Dutch
Dutch  Svenska
Svenska  Português
Português  Italiano
Italiano  Español
Español  Français
Français  Suomalainen
Suomalainen  Български
Български  Românesc
Românesc  Magyar
Magyar  Eesti
Eesti  Ελληνική
Ελληνική  Latviešu
Latviešu  Lietuvių
Lietuvių  やまと
やまと  中国
中国  Dansk
Dansk  Türkçe
Türkçe  ID
ID  Українська
Українська  한국어
한국어  Norsk
Norsk  Peter Sommer
Peter Sommer 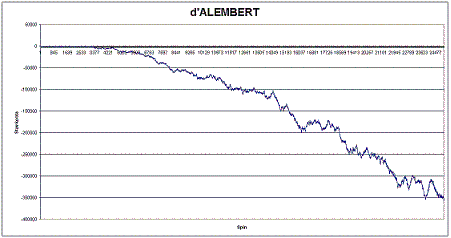






You have to be logged in to add a comment