The Fibonacci system is one of the most famous and most commonly used betting systems. You bet on colors with the progression following the Fibonacci sequence. The Fibonacci sequence is cumulative.  The next number is equal to the sum of the two previous ones: 1, 1, 2, 3, 5, 8, 13, 21, 34, and so forth.  This is a type of “cross-out system”. When you start playing, it’s useful to write down a sequence of numbers according to the Fibonacci principle. If you win, you cross out the last two numbers in the sequence.  If you lose a round, you write down a number corresponding with the bet size in the sequence, and consequently, you bet the sum of the last two numbers. It is important to understand, that the sequence ends once you are back to betting 1 unit (if you cross out all numbers in a sequence, you win 1 unit).

What do the statistics say?

In principle, it is very interesting and at first sight, the system seems to be reliable. Whilst writing down and crossing out a sequence of numbers, you notice that if you lose, ONE number is added to the sequence, but if you win, TWO numbers are crossed out from the sequence. Due to the fact that you are betting on the probability of (almost) 50%, the proportion of wins and losses occurring is roughly the same in the long term (but the number of wins is fewer than the number of losses because of the “zero”). This leads to enormous pressure to cross out the whole sequence to make a profit of 1 unit. It looks good. So let’s see how it looks in reality.

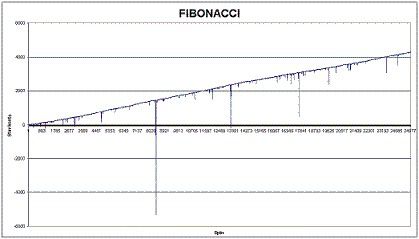
Unsurprisingly the progression went exactly as we had assumed. The progression constantly went to a plus and permanently made a profit of about 4.000 units per 25.000 spins. The only problem was the negative “hairs” hanging from the curve. These short-term local slumps are typical of the Martingale effect. In these local slumps, the proportion of “good” and “bad” colors exceeded the ratio of 2:1 (the roulette hit blacks more often than reds). The Fibonacci system is characterized by a gentle progression in the beginning and consequently, it turns to aggressive growth. However, let’s see how the sequence proceeded: ….34, 55, 89, 144, 233, 377, 610, 987, 1597, and so on.  It grew pretty fast, so if the slump was large enough, it went deeply below zero and even reached values of 100 000 to 1000 000 units.  Therefore there was a risk of bankruptcy.

To avoid the big slumps, we attempted to apply some limitations such as a maximum series length. Our limitations were to the 10th and 15th number in the sequence – this means that if we reached the tenth or fifteenth number in the Fibonacci sequence (i.e. 66 and 610 units); we reset the game back to 1 unit:

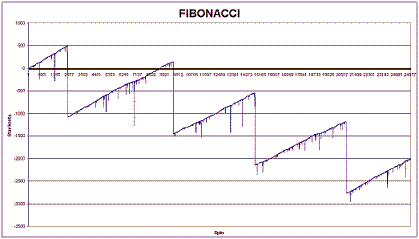
As the graph shows, the outcome was a downward curve. The higher the limitation, the “more serrated” graph was, and if we had used bigger limitations, the curve would have been the same as a progression with unlimited betting. Unfortunately, in both of these cases, the progression went below zero and reached values of about 1000 units.

However, we tried to apply a cascade progression in the series: after each unsuccessful streak we increased the size of the bet by 1 unit (we applied limitations to 10 numbers in a sequence):

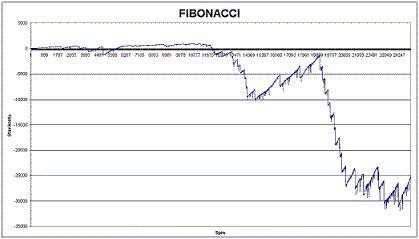
Unfortunately, this did not turn out to be successful either. There were sequences of growth, but basically, the progression always went below zero. Generally, we can observe that if the system is unlimited, it continually yields a profit but rapid local slumps are always present. If we apply limitations to the system, there is always a downward trend, even when using arithmetic progression. By using an aggressive progression (Martingale progression) the system grows, but again there are slumps. These slumps are not as significant as when using unlimited betting.

The following graph shows another demonstration of the progression using a limitation of 10 numbers in a sequence by employing the Martingale progression:

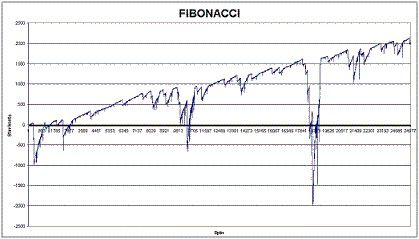
This graph shows that this system requires further work and improvement if it is to be usable in the long term.

Moreover, we have prepared a roulette betting simulator, where you can try this system for free.