First of all, let's say when this magic formula can be used. There is a basic rule that says Kelly should only be counted if there is a positive expected value. In other words, only if the investor or bettor has a mathematical advantage.
We deliberately mention the word investor here at the beginning, because Kelly's criterion is equally well applicable to financial markets. However, we will not deal with this too much in today's article. Instead, let's look at Kelly's use in gambling.
If you are a regular reader of our articles, you already know that Kelly will only be able to apply to two games of chance. And that's blackjack and Wild Deuces video poker. Other games, such as roulette or slots, always have a mathematical advantage on the casino side. Of course, the exceptions are progressive jackpots, where the jackpot grows enough to shift the advantage to the player.
The Formula for Kelly's Criterion
Now that we've covered the basics, let's look at the calculation:
F - part of the bankroll we should bet
p - chance of winning in decimal numbers (eg 80% = 0.8%)
B - payout ratio (e.g. if the payout ratio is 35 to 1 as in roulette, we substitute 35 for B)
We will immediately look at a simple example of a coin flip with a payout ratio of 2 to 1 for the bettor. The expected value in this case is 0.5 (EV = (2 * 0.5) - (1 * 0.5)). This is a positive number, so we can move on to calculating Kelly's bet. In this case, P will be 0.5 (coin flip is 50% to 50%) and B will be 2 (payout ratio is 2 to 1):
The result was 0.25, and after converting to a percentage, in this particular case, we should bet 25% of our total bankroll.
For the sake of argument, we can still show what happens when we try to calculate Kelly's bet for a game with a negative advantage for the player. For example, let's choose a colour bet on American roulette, where the casino's edge is 5.26%.
P = 0.4737
B = 1
The result was -0.0526, i.e. -5.26%. So the player should not bet anything. Respectively, bet 5.26% on your loss, which of course does not work that way.
Kelly's Criterion in Blackjack
5.26% is a fairly specific number that many advanced players know. This is a house edge in American roulette. If it is a straight bet, the whole equation is simplified, and Kelly's criterion is equal to the expected value.
Which gives us an excellent idea to calculate the optimal bet for blackjack. There, the basic game pays 1 to 1, and thanks to card counting, the player knows his advantage. In a very simplified situation, the optimal bet will be equal to the current advantage.
If you want to be more precise, you need to adjust Kelly's blackjack bet by dispersion, which is caused by doubling and splitting the cards. Therefore, you should optimally bet only 76% of the expected value.
| True Count | Players advantage | % optimal bet |
| -1 and less | -1 % and less | 0% |
| 0 | -0.5% | 0% |
| 1 | 0% | 0% |
| 2 | 0.5% x 0.76 | 0.38% |
| 3 | 1% x 0.76 | 0.76% |
| 4 | 1.5% x 0.76 | 1.14% |
| 5 | 2% x 0.76 | 1.52% |
| 6 | 2.5% x 0.76 | 1.9% |
| 7 | 3% x 0.76 | 2.28% |
For a more comprehensive explanation of how to calculate your blackjack bet, see our older article on money management.
Kelly's Criterion in Video Poker
Another casino game in which we get the positive advantage of the player is video poker Deuces Wild, where the player can get an advantage of 0.76% with the optimal strategy. Here, however, there is quite a problem. It is far from a game with a payout ratio of 1 to 1, as was the case with blackjack. Most professional gamblers use a modified formula to calculate the optimal bet in video poker, in which they simply divide the player's advantage by the dispersion of the game.
- Deuces Wild Video Poker
- Player Advantage: 0.76%
- Dispersion: 25.83
Which gives us 0.0076 / 25.83 = 0.00029. After converting to a percentage, we find that the optimal bet for Deuces Wild Video Poker is 0.029% of the bankroll. The bet amount will not change during the game. In absolute numbers, let's count with a bankroll of €/$ 10,000, so we should bet €/$ 290 per turn.

 EN
EN  čeština
čeština  Polski
Polski  Slovenčina
Slovenčina  Русский
Русский  Deutsch
Deutsch  Slovenski
Slovenski  Dutch
Dutch  Svenska
Svenska  Português
Português  Italiano
Italiano  Español
Español  Français
Français  Suomalainen
Suomalainen  Български
Български  Românesc
Românesc  Magyar
Magyar  Eesti
Eesti  Ελληνική
Ελληνική  Latviešu
Latviešu  Lietuvių
Lietuvių  やまと
やまと  中国
中国  Dansk
Dansk  Türkçe
Türkçe  ID
ID  Українська
Українська  한국어
한국어  Norsk
Norsk  Peter Sommer
Peter Sommer 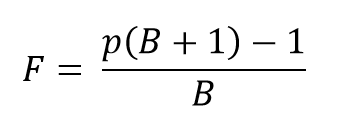
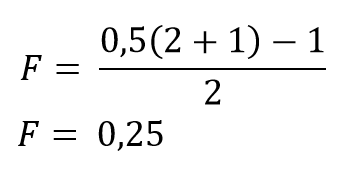
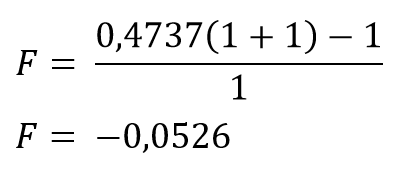






You have to be logged in to add a comment