概率和赌场游戏
 Peter Sommer
Peter Sommer
你了解你的机会吗?如果你要在赌场玩,你应该确保你知道你的机会,并完全理解它们。为什么?因为概率是使赌场运作的引擎。没有概率,赌博业就不可能存在。
机会只是某事发生的概率。概率是我们日常生活的一部分。当我们决定在红灯时穿过一条繁忙的街道时,有一定的机会会被汽车撞到,但作为回报,我们有机会更快地穿过街道,并获得一些时间。
当我们赌博时,我们估计某一事件发生的概率,以制定我们的赌注。正是在这些情况下,我们才计算出概率。
💡 概率实例
假设我们有一个装有四个球的袋子,其中只有一个是红色的,其他三个是蓝色的。不看就只掏出红球的概率是1/4。
有几种方法来表达概率。我们也可以说,对红球有3/1的机会,因为平均每抽出一个红球,我们就抽出三个蓝球。
我们也可以用百分比来表示我们的机会,所以如果有100%的机会抽到红球,我们抽到红球的概率是25%。因此,100除以4得到的是25%。
如果有三个蓝球,抽到蓝球的概率是75%,有25%的概率。
赌场游戏的概率
赌场的运作原则是,考虑到我们的长期结果,提供的赔率并不那么好。
一袋气球的例子是显示赌场如何运作的一个简单方法。假设一家赌场提供的抽到红球的赔率是3。如果你下注5美元,那么平均而言,在四次尝试中,你将拉动蓝球3次,输掉15美元,第四次拉动红球,赢得10美元,但赌场仍会有5美元的亏损。
所有的赌博都只是关于概率。任何有经验的赌徒
都会告诉你这一点。因此,熟悉这些数字并知道如何使用它们是至关重要的。因此,在这里我们现在将告诉你如何计算赌博中的概率。如果你正确理解这个原理,你可以用它来计算其他任何事物的概率。
轮盘赌的概率
轮盘赌就像财富之轮。而你知道为什么吗?只需要3个字来解释--大数理论。每个经营赌场或制作在线赌场游戏的人都非常了解这一理论。因为这与他的收入直接相关。而且,由于它的存在,从长远来看,赌场也总是赢过赌徒。一切都与概率和房子的边缘有关。
📌 注:文章中的所有数字都是指欧洲轮盘赌--所以我们算37个数字。
如何书写概率
有几种写概率的方法。最著名的可能是百分比。除此以外,还使用了使用分数或比率的表达方式。
- 表示为百分比(%)--这里没有什么好补充的,只是为了完整起见,这是选定事件的百分比。它的计算方法是(部分/总数)*100。例如,在轮盘上击中所选号码的概率(直):1/37*100=2.7%。
- 用分数表达(1/x)--当用分数表达概率时,我们说该现象在X次试验中发生1次。在数字表达中,我们依靠计算百分比。如果我们考虑上述1/37的例子,这意味着轮盘上统计学上选定的数字在37次旋转中会有1次落下。
- 用比率表达(X与1)--每当X发生时,所选现象就会发生1次。在这里,我们再次坚持使用轮盘赌所选数字的概率。在这种情况下,比率将被写成36比1。这意味着,在每36次旋转中,数字没有落下,就会有一次所选数字落下的情况。
📌 注:正如大数理论所说,概率本质上是一种数学极限。随着试验越来越多,你现实地越来越接近计算结果。
正如你所看到的,使用分数的表达方式和使用比率的表达方式非常相似。唯一的区别是,分数计算所有的旋转,而比率则是将总的旋转分成两类。
轮盘赌中单个赌注的概率表
|
赌注 |
摘自 |
比率 |
百分比 |
|
直接下注 |
1/2,055 |
1.055比1 |
48,6 % |
|
栏目 |
1/3,08 |
2.08比1 |
32,4 % |
|
一打 |
1/3,08 |
2.08比1 |
32,4 % |
|
六线 |
1/6,17 |
5.17比1 |
16,2 % |
|
角落 |
1/9,25 |
8.25比1 |
10,8 % |
|
街道 |
1/12,33 |
11.33比1 |
8,1 % |
|
分割 |
1/19,5 |
18.5比1 |
5,4 % |
|
直线 |
1/37 |
36比1 |
2,7 % |
直线投注的概率
对所选现象的重复性进行数学比较也可能是有趣的。在这种情况下,我们选择了一个直接的赌注,具体来说,比如赌红色。那么,比如说,连续5次出现红色的变化概率会是多少?
|
转动的次数 |
比率 |
百分比 |
|
1 |
1.06比1 |
48,6 % |
|
2 |
3.23比1 |
23,7 % |
|
3 |
7.69比1 |
11,5 % |
|
4 |
16.9比1 |
5,6 % |
|
5 |
35.7比1 |
2,73 % |
|
6 |
74.4比1 |
1,33 % |
|
7 |
154比1 |
0,65 % |
|
8 |
318比1 |
0,31 % |
|
9 |
654比1 |
0,15 % |
|
10 |
1 346比1 |
0,074 % |
|
15 |
49 423比1 |
0,002 % |
|
20 |
1 813 778转1 |
0,000055 % |
可以看出,随着旋转数的增加,这种现象的概率迅速下降。然而,请记住,这些概率是对整个现象的描述。随机数生成器不考虑以前的结果,因此,即使红色连续击中20次的游戏系列每181.3万个游戏中出现一次,21个游戏轮次的房子边缘和概率(即48.6%)将与其他游戏轮次相同。
在这种情况下,往往会遇到 "玩家谬误 "一词,即投注者认为如果一种颜色连续被击中几次,那么在下一次旋转中,另一种颜色被击中的概率就会更高。在现实中,情况并非如此。这种谬论最著名的案例是1913年在蒙特卡洛赌场观察到的,当时轮盘上的黑色连续落下26次,在这一不可思议的连胜过程中,甚至在连胜结束后,人们都疯狂地投注红色。这时,赌场赚了一些非常漂亮的钱。
注:一种颜色连续被击中26次的概率为0.000000730870%,在6700万局中出现一次。
如何计算轮盘赌的概率
想知道更多个人投注的赔率吗?试着自己计算一下。使用百分比和概率的工作并不十分复杂。一般来说,最简单的方法是从分数开始,用它们来进一步计算百分比和比率。例如,如果你想在分数中计算红色的情况下的概率,你要做以下工作。
比赛场地上的红人总数/比赛场地总数=18/37
一个旋转的概率
同样,一个简单的规则适用于此。只需计算出能让你赢的场次,然后除以场次总数。
比如说。
- 颜色 - 18/37
- Sudá/Lichá - 18/37
- 一打 - 12/37
- 数字0-1/37
- 黑色和偶数 - 9/37(比赛场地中只有9个数字既是黑色又是偶数)。
- 一打和一列 - 4/37(一打和一列中只有4个数字)。
就像赢的概率一样,你可以计算出输的概率。只需计算非赢家的场次,然后再除以场次总数。例如,如果你赌红色,输的概率是19/37(18个黑场+绿零)。
注意:要将分数减为1/x,只需将分子和分母除以分子。例如,18/37(你用两个数字除以18)在调整后将是1/2.055。因此,这意味着每2.055个回合,就有一个回合会出现红色或黑色的结果。
多次旋转的概率
一旦你掌握了单次旋转的计算方法,计算多次旋转的概率就非常简单。只要把各个分数互相相乘就可以了。
例子。
- 旋转 - 赌红色=18/37
- 旋转-每打的赌注=12/37
两轮都赢的概率=(18/37)*(12/37)=1/6.34或15.77%或5.34比1
- 旋转 - 直线投注 - 1/37
- 旋转 - 直线投注 - 1/37
两轮都赢的概率=(1/37)*(1*37)=1/1369或0.073%或1368比1
- 旋转 - 赌黑色和奇数9/37
- 旋转 - 赌偶数18/37
- 转动 - 栏目投注 12/37
3轮全胜的概率=(9/37)*(18/37)*(12/37)=1/26.06或3.84%或25.06比1
条目之间的实际转换又非常容易。你通过将分数除以1/x的形式,然后乘以100,就可以得到百分比。你通过从分母中减去1,得到X到1的比例记号,分母是总的获胜回合。见该段上方的例子。
骰子的概率
骰子是另一种机会游戏,计算其赔率相对容易。在计算掷骰子的胜率之前,我们先看看骰子掷出的概率本身。
骰子有6个面。因此,任何数字下降的机会是1/6。骰子的传统玩法是用两个骰子。因此,任何两个数字组合的几率是2/36。然而,我们对具体的数字并不感兴趣,而是对这些数字的总和感兴趣,这在骰子中更为重要。我们再一次使用这个公式:获胜组合数/所有组合数。
假设我们想知道和为7的概率,获胜的组合:(1-6),(2-4),(3-3),(4-2),(6-1)。正如你所看到的,总共有6种不同的组合,其中7的总和可以在两个骰子上掷出。由于所有组合的数量是36,7的概率是6/36=0.1666
这样一来,所有其他可能的结果都可以轻松计算出来。
|
共计 |
概率 |
|
2 |
1/36 |
|
3 |
2/36 |
|
4 |
3/36 |
|
5 |
4/36 |
|
6 |
5/36 |
|
7 |
6/36 |
|
8 |
5/36 |
|
9 |
4/36 |
|
10 |
3/36 |
|
11 |
2/36 |
|
12 |
1/36 |
骰子赢钱的几率
简单地说,我们来看看骰子的规则。最常见的赌注是过关线。
- 如果你掷出7或11,你就赢了
- 如果你掷出2、3或12,你就输了。
- 在其他情况下(4,5,6,8,9或10),一个点被确定并滚动,直到该点被再次滚动(赢)或一个7被滚动(输)。
我们首先计算获胜的概率,然后再确定点数。打中7的机会是6/36,打中11的机会是2/36。然后这两个分数必须相加,得出3/36+2/36=2/9=0.2222。
现在我们把注意力转向确定了一个点的情况。也就是说,当点数为4、5、6、8、9或10时。让我们从总共4个开始。
如果掷出的是4,则确定一个点数,玩家继续掷,直到掷出4或7。这就是我们进入条件概率领域的地方。这告诉我们,如果事件B同时发生,事件A的概率是多少。在我们的例子中,它将是如果这一轮结束(掷出4或7),我们赢(掷出4)的概率是多少。然后我们将这些值插入公式中。
- P(A)=4的瀑布之和:3/36
- P(A∩B)= 经过调整,我们发现它等于A
- P(B)=瀑布4或7:3/36 + 6/36 = 9/36
由此可见,。
- P(4|4或7)=(3/36)/(9/36)=1/3
用类似的方法,我们可以计算出5、6、8、9和10的总和
- P(5|5或7)=(4/36)/(10/36)=2/5
- P(6|6或7)=(5/36)/(11/36)=5/11
- P(8|8或7)=(5/36)/(11/36)=5/11
- P(9|9或7)=(4/36)/(10/36)=2/5
- P(10|10或7)=(3/36)/(9/36)=1/3
现在我们可以计算出赢钱的机会,即确定点数时的原始卷和玩家赢钱时的下一次卷的概率。
- 原始卷4 x P(4|4或7) = 3/36 x 1/3 = 1/36
- 原始卷5 x P(5|5或7) = 4/36 x 2/5 = 2/45
- 原始卷6 x P(6|6或7) = 5/36 x 5/11 = 25/396
- 原始卷8 x P(8|8或7) = 5/36 x 5/11 = 25/396
- 原卷9 x P(9|9或7) = 4/36 x 2/5 = 2/45
- 原始卷10 x P(10|10或7) = 3/36 x 1/3 = 1/36
所有这些分数都给了我们赢的概率,如果第一次滚动是4,5,6,8,9或10。如果你想知道通关线投注的总赢钱概率,你需要把它们加起来,再加上点前的赢钱概率(掷出7或11 - 2/9)。
2/9 + 1/36 + 2/45 + 25/396 + 25/396 + 2/45 + 1/36 = 244/495
因为244/495正好是49.3%。这还不到50%。事实上,你可能找不到一个更好的机会来赢得1/1的赔率。也许除了21点,如果你会算牌。
21点的概率
21点是机会游戏,其中赔率最重要。在21点中,你可以用你的技能和知识影响房子的边缘。你只需要知道这方面的最佳策略,如果你知道如何算牌,你甚至会以玩家的优势来玩。左右,你实际上不需要知道所有具体的概率,因为所有这些计算已经被你之前的数学家做了,他们想出了21点的所有战术和策略。
然而,为了兴趣,我们将展示如何计算21点中一些重要现象的概率。
如果我们从一副扑克牌的角度来看待概率问题,很明显,可能的结果数量会迅速增加。21点是用一副52张牌,4种花色和13种价值来玩的。这就得出了以下几率。
- 我从甲板上抽出一张A(或任何单独的牌):4/52=0.0769(69%)。
- 我从甲板上抽出一张黑桃:13/52=0.25(25%)。
然而,与掷硬币、轮盘赌或老虎机等不同,一副牌有一些 "记忆"。或者说,这意味着以前的结果对现在和未来的行动有影响。这是因为有一张牌从牌库中掉了出来,这就改变了起始情况。让我们看一个例子,从52张牌中抽出的第一张牌是A(7.69%的概率)。现在,A被再次抽出作为第二张牌的概率将有所不同。第一次抽牌后,A的数量下降到3,牌的数量下降到51。
21点的概率 自然
每个玩家都会首先关注的是21点的概率。也就是说,玩家在这一轮开始时得到一张A和一张10的概率是多少--换句话说,就是自然。
这种情况有两种方式,如果我们把这两种方式加起来,就可以得到我们的21点的赔率。
📌 注意:我们是为单副21点计数。所以52张牌,4张A和16张10。庄家的牌是不可见的,所以不会影响概率。
- 玩家收到第一张A和一张10牌
玩家发第一张A牌,概率为4/52。因此,玩家必须拿到第二张牌的10,为此的赔率是16/51。这两个概率必须相互相乘,才能得到16/663。
- 玩家收到第一张10牌和一张A牌
玩家收到第一张价值为10的牌的概率是16/52。之后玩家得到A的几率是4/51。乘法后,我们得到16/663。
如果我们想知道得到21点的概率,我们只需将这两个现象相加。所以16/663 + 16/663 = 32/663 = 4.827%。换句话说,一个玩家大约每20手就能得到一次21点。你可以用类似的方法计算多牌桌的概率,这一点我们已经为你做了。
|
包裹的数量 |
概率 |
|
1 |
4,827 % |
|
2 |
4,780 % |
|
3 |
4,764 % |
|
4 |
4,757 % |
|
5 |
4,752 % |
|
6 |
4,749 % |
破产的概率
知道你破产的几率有多大可能也很有趣。同样,我们将重点讨论一个例子,即你在单副牌桌上只和庄家玩的情况。我们来看看一个非常简单的情况,一个玩家有2张价值10的牌,所以他有20分。在玩家得到第三张牌的情况下,已经从甲板上打了3张牌。这样一来,甲板上就剩下49张牌了。在这49张牌中,只有4张A可以帮助你。在这49张中,有45张是不需要的。因此,爆仓的几率是45/49=0.9183673。
你可以用类似的方法计算其他概率。你总是要能够正确地想象情况。这就是全部。
|
手的价值 |
破产的概率 |
|
21 |
100 % |
|
20 |
92 % |
|
19 |
85 % |
|
18 |
77 % |
|
17 |
69 % |
|
16 |
62 % |
|
15 |
58 % |
|
14 |
56 % |
|
13 |
39 % |
|
12 |
31 % |
|
少了11个 |
0 % |
接下来让我们看看庄家在每张牌上爆牌的可能性有多大。
|
手的价值 |
破产的概率 |
|
2 |
35,30 % |
|
3 |
37,56 % |
|
4 |
40,28 % |
|
5 |
42,89 % |
|
6 |
42,08 % |
|
7 |
25,99 % |
|
8 |
23,86 % |
|
9 |
23,34 % |
|
10, J, Q, K |
21,43 % |
|
ǞǞǞ |
11,65 % |
扑克的概率
扑克是另一种概率极其重要的纸牌游戏。在其他方面。因此,让我们来看看你在扑克中的机会是什么。
翻牌前的概率
现在我们已经概述了概率在一副牌中的作用,让我们来谈谈实际应用。首先,我们将展示如何计算一手牌中耗尽对子的概率。例如,备受关注的Ace)。在这种情况下,我们需要将这些概率相互相乘。
(4/52) x (3/51) = (12/2652) = (1/221) = 0,004524 (0,45 %)
注意:如果你在一个每小时发30手牌的赌场玩扑克,你大约每7个半小时就会得到一对A。
那么,当你发牌时,得到13个可能的对子中任何一个的机会是什么?我们可以假设每一对个体的赔率是1/221(见上面的公式)。这些对子总共可以有13个,所以计算公式为13/221=0.0588。所以你可以期待大约每35场比赛就有一对。
扑克中玩家对玩家的概率
然而,扑克是一种多人游戏,通常是互相对战。因此,这里选择了最常见的翻牌前情况。
|
你的手 |
你的对手的手 |
赢的概率 |
|
高对 |
两张低牌 |
83 % |
|
高对 |
低位对 |
82 % |
|
中间一对 |
高、低牌 |
71 % |
|
两张大牌 |
两张低牌 |
63 % |
|
两张大牌 |
低位对 |
55 % |
通过 "出局 "计算概率
如果你设法看到翻牌的牌,你肯定会进一步关心你提高手牌的机会是什么。在这种情况下,我们将谈一谈所谓的 "出局"。在扑克中,这个术语指的是任何可以帮助你的牌。这种常见的情况可能是当一个玩家持有两张花色的牌,而翻牌时又出现两张相同花色的牌。然后,玩家有4张同花顺,因此有9张出局,剩下9张牌可以组成同花顺。
|
出局人数 |
翻牌 - 转牌 |
转弯 - 河流 |
转动河流 |
|
20 |
42,6 % |
43,5 % |
67,5 % |
|
19 |
40,4 % |
41,3 % |
65,0 % |
|
18 |
38,3 % |
39,1 % |
62,4 % |
|
17 |
36,2 % |
37,0 % |
59,8 % |
|
16 |
34,0 % |
34,8 % |
57,0 % |
|
15 |
31,9 % |
32,6 % |
54,1 % |
|
14 |
29,8 % |
30,4 % |
51,2 % |
|
13 |
27,7 % |
28,3 % |
48,1 % |
|
12 |
25,5 % |
26,1 % |
45,0 % |
|
11 |
23,4 % |
23,9 % |
41,7 % |
|
10 |
21,3 % |
21,7 % |
38,4 % |
|
9 |
19,1 % |
19,6 % |
35,0 % |
|
8 |
17,0 % |
17,4 % |
31,5 % |
|
7 |
14,9 % |
15,2 % |
27,8 % |
|
6 |
12,8 % |
13,0 % |
24,1 % |
|
5 |
10,6 % |
10,9 % |
20,3 % |
|
4 |
8,5 % |
8,7 % |
16,5 % |
|
3 |
6,4 % |
6,5 % |
12,5 % |
|
2 |
4,3 % |
4,3 % |
8,4 % |
|
1 |
2,1 % |
2,2 % |
4,3 % |
📌注意:有一个非常简单的方法来计算出局的概率,所以你可以在赌桌上直接做。它一般被称为 "四二 "规则。翻牌后,玩家只需将出牌数乘以4,就能找到转牌和河牌的概率。如果他在转牌时没有拿到这张牌,他只需将出牌数乘以2,就可以得到在河牌时拿到这张牌的大概概率。
同样,我们可以用翻牌后有4张相同花色的牌为例。所以你的出牌是9张,转牌和河牌后同花的概率是36%(9x4)。假设你在这一回合没有得到一张牌。在这种情况下,我们将出局数乘以2,发现我们有18%(9x2)的机会在河牌时用完牌。通过对比表格你可以看到,这种方法确实很简单,但另一方面也不准确,但可以使用。

 CN
CN  English
English  čeština
čeština  Polski
Polski  Slovenčina
Slovenčina  Русский
Русский  Deutsch
Deutsch  Slovenski
Slovenski  Dutch
Dutch  Svenska
Svenska  Português
Português  Italiano
Italiano  Español
Español  Français
Français  Suomalainen
Suomalainen  Български
Български  Românesc
Românesc  Magyar
Magyar  Eesti
Eesti  Ελληνική
Ελληνική  Latviešu
Latviešu  Lietuvių
Lietuvių  やまと
やまと  Dansk
Dansk  Türkçe
Türkçe  ID
ID  Українська
Українська  한국어
한국어  Norsk
Norsk 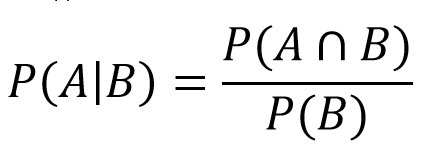


你必须是登录才能添加评论