Iespējamība un kazino spēles
 Peter Sommer
Peter Sommer
Vai saprotat savas iespējas? Ja gatavojaties spēlēt kazino, jums jāpārliecinās, ka zināt savas izredzes un pilnībā tās saprotat. Kāpēc? Tā kā varbūtība ir dzinējspēks, kas nodrošina kazino darbību. Bez varbūtības azartspēļu nozare nebūtu iespējama.
Varbūtība ir vienkārši varbūtība, ka kaut kas notiks. Iespējamība ir daļa no mūsu ikdienas dzīves. Ja mēs nolemjam šķērsot kustīgu ielu pie sarkanās gaismas, pastāv zināma iespēja, ka mūs notrieks automašīna, taču pretī mums ir iespēja šķērsot ielu ātrāk un iegūt nedaudz laika rezervē.
Kad mēs spēlējam azartspēles, mēs aplēšam noteikta notikuma iespējamību, lai formulētu savu likmi. Šādos gadījumos mēs aprēķinām varbūtību.
💡 Iespējamības piemērs
Pieņemsim, ka mums ir maisiņš, kurā ir četras bumbiņas, no kurām tikai viena ir sarkana, bet pārējās trīs ir zilas. Varbūtība, ka, nemeklējot izvilksiet tikai sarkano bumbiņu, ir 1 pret 4.
Ir vairāki veidi, kā izteikt varbūtību. Varam arī teikt, ka ir 3 pret 1 iespēja pret sarkano, jo vidēji uz katru izlozēto sarkano bumbiņu tiek izlozētas trīs zilas bumbiņas.
Mēs varam izteikt mūsu izredzes arī procentos, tātad mūsu varbūtība, ka tiks izlozēta sarkanā bumbiņa, ir 25%, ja ir 100% varbūtība, ka tiks izlozēta sarkanā bumbiņa. Tātad, 100 dalot ar četri, iegūstam 25%.
Ja ir trīs zilas bumbiņas ar 25% izlozes varbūtību, varbūtība, ka tiks izlozēta zila bumbiņa, ir 75%.
Kazino spēļu varbūtība
Kazino darbojas pēc principa, piedāvājot izredzes, kas nav tik labi, ņemot vērā mūsu ilgtermiņa rezultātu.
Piemērs ar balonu maisu ir vienkāršs veids, kā parādīt, kā darbojas kazino. Pieņemsim, ka kazino piedāvā 3 izredzes uz sarkanas bumbiņas izlozi. Ja Jūs uzliekat 5$, tad četros mēģinājumos Jūs vidēji trīs reizes izspēlēsiet zilo bumbiņu un zaudēsiet 15$, bet ceturtajā reizē Jūs izspēlēsiet sarkano bumbiņu un vinnēsiet 10$, bet kazino joprojām būs "melnajā" par 5$.
Visas azartspēles ir saistītas tikai ar varbūtību. To jums apstiprinās jebkurš pieredzējis spēlmanis. Tāpēc ir svarīgi šos skaitļus pārzināt un zināt, kā ar tiem strādāt. Šeit mēs jums parādīsim, kā aprēķināt varbūtību azartspēlēs. Ja jūs pareizi saprotat šo principu, varat to izmantot, lai aprēķinātu jebkādu citu varbūtību.
Ruletes varbūtība
Rulete ir kā laimes rats. Un jūs zināt, kāpēc? Lai to izskaidrotu, nepieciešami tikai trīs vārdi - lielo skaitļu teorija. Šo teoriju ļoti labi zina ikviens, kas vada kazino vai veido tiešsaistes kazino spēles. Jo tas ir tieši saistīts ar viņa ienākumiem. Un, pateicoties tam, kazino ilgtermiņā vienmēr uzvar arī pār likmju veicējiem. Viss ir saistīts ar varbūtību un kazino priekšrocību.
📌 Piezīme: visi rakstā minētie skaitļi attiecas uz Eiropas ruleti - tātad mēs skaitām 37 skaitļus.
Kā rakstīt varbūtību
Ir vairāki veidi, kā rakstīt varbūtību. Iespējams, vispazīstamākais ir procentuālais īpatsvars. Papildus šiem izteicieniem tiek izmantotas arī izteiksmes, kurās tiek izmantota daļa vai attiecība.
- Izteikts procentos (%) - šeit nav daudz ko piebilst, bet tikai pilnīguma labad, šis ir izvēlētā notikuma procentuālais rādītājs. To aprēķina kā (daļa/kopējais)*100. Piemēram, varbūtība, ka uz ruletes rata trāpīs izvēlētais skaitlis (taisni): 1/37*100=2,7%.
- Izteiksme, izmantojot daļskaitļus (1/x) - Izsakot varbūtību ar daļskaitļiem, mēs sakām, ka parādība notiek 1 reizi no X mēģinājumiem. Skaitliskā izteiksmē mēs paļaujamies uz procentuālu aprēķinu. Ja ņemam vērā iepriekš minēto piemēru 1/37, tas nozīmē, ka statistiski izvēlēts skaitlis uz ruletes rata kritīs 1 reizi 37 griezienos.
- Izteiksme ar attiecību (x pret 1) - katru reizi, kad notiek X, izvēlētā parādība notiek 1 reizi. Arī šajā gadījumā mēs izmantojam ruletei izvēlēto skaitļu varbūtību. Šajā gadījumā attiecība tiks rakstīta kā 36 pret 1. Tas nozīmē, ka pēc katriem 36 griezieniem, kuros skaitlis nav iekritis, būs viens gadījums, kad iekritīs izvēlētais skaitlis.
📌 Piezīme: Kā teikts lielo skaitļu teorijā, varbūtība būtībā ir matemātiska robeža. Veicot arvien vairāk izmēģinājumu, jūs reāli pietuvojaties aprēķinātajam rezultātam.
Kā redzat, izteiksmes, kurās tiek izmantotas frakcijas, un izteiksmes, kurās tiek izmantotas attiecības, ir ļoti līdzīgas. Vienīgā atšķirība ir tāda, ka frakcija skaita visus griezienus, bet attiecība sadala kopējo griezienu skaitu divās kategorijās.
Atsevišķu likmju varbūtību tabula ruletē
|
Likme |
Izvilkums no |
Attiecība |
Procenti |
|
Tieša likme |
1/2,055 |
1,055 līdz 1 |
48,6 % |
|
Kolonna |
1/3,08 |
2,08 pret 1 |
32,4 % |
|
Ducis |
1/3,08 |
2,08 pret 1 |
32,4 % |
|
Sešas līnijas |
1/6,17 |
5,17 pret 1 |
16,2 % |
|
Stūris |
1/9,25 |
8,25 pret 1 |
10,8 % |
|
Ielas |
1/12,33 |
11,33 pret 1 |
8,1 % |
|
Split |
1/19,5 |
18,5 pret 1 |
5,4 % |
|
Taisni |
1/37 |
36 pret 1 |
2,7 % |
Tiešās likmes varbūtība
Interesants varētu būt arī izvēlētās parādības atkārtošanās matemātisks salīdzinājums. Šajā gadījumā mēs esam izvēlējušies tiešo likmi, piemēram, likmi uz sarkano krāsu. Tātad, kāda būs, piemēram, sarkanās krāsas maiņas varbūtība 5 reizes pēc kārtas?
|
Griezienu skaits |
Attiecība |
Procenti |
|
1 |
1,06 pret 1 |
48,6 % |
|
2 |
3,23 pret 1 |
23,7 % |
|
3 |
7,69 pret 1 |
11,5 % |
|
4 |
16,9 pret 1 |
5,6 % |
|
5 |
35,7 pret 1 |
2,73 % |
|
6 |
74,4 pret 1 |
1,33 % |
|
7 |
154 pret 1 |
0,65 % |
|
8 |
318 līdz 1 |
0,31 % |
|
9 |
654 pret 1 |
0,15 % |
|
10 |
1 346 līdz 1 |
0,074 % |
|
15 |
49 423 pret 1 |
0,002 % |
|
20 |
1 813 778 līdz 1 |
0,000055 % |
Kā redzams, palielinoties griezienu skaitam, šīs parādības varbūtība strauji samazinās. Tomēr paturiet prātā, ka šīs varbūtības raksturo parādību kopumā. Nejaušo skaitļu ģenerators neņem vērā iepriekšējos iznākumus, tāpēc, lai gan spēles sērija, kurā sarkanā krāsa ir 20 reizes pēc kārtas, notiek reizi 1,813 miljonos spēļu, 21 spēles raundā kazino priekšrocības un varbūtība būs tāda pati (t. i., 48,6 %) kā katrā citā spēles raundā.
Bieži vien šajā gadījumā var sastapties ar spēlētāja maldināšanu, kad likmju veicējs uzskata, ka, ja viena krāsa ir trāpījusi vairākas reizes pēc kārtas, pastāv lielāka varbūtība, ka nākamajā griezienā trāpīs cita krāsa. Patiesībā tas tā nav. Slavenākais šīs kļūdas gadījums tika novērots 1913. gadā Montekarlo kazino, kad uz ruletes rata 26 reizes pēc kārtas krita melnā krāsa, un gandrīz visu šīs neticamās sērijas laiku un pat pēc tās beigām cilvēki drudžaini lika likmes uz sarkano krāsu. Tad kazino nopelnīja ļoti labu naudu.
📌 Piezīme: varbūtība, ka viena krāsa tiks trāpīta 26 reizes pēc kārtas, ir 0,000000730870%, un tas notiek reizi 67 miljonos spēļu.
Kā aprēķināt ruletes varbūtību
Vēlaties uzzināt vairāk individuālo likmju koeficientu? Pamēģiniet tos aprēķināt paši. Darbs ar procentiem un varbūtībām nav ļoti sarežģīts. Visvienkāršākais veids ir sākt ar daļskaitļiem un izmantot tos, lai aprēķinātu turpmākos procentus un attiecības. Piemēram, ja vēlaties aprēķināt varbūtību, kas izteikta kā daļskaitlis, situācijai, kurā sarkanā krāsa ir sarkana, rīkojieties šādi:
Kopējais sarkano laukumu skaits uz spēles laukuma/kopējais spēles laukumu skaits = 18/37
Viena grieziena varbūtība
Arī šajā gadījumā ir spēkā vienkāršs noteikums. Vienkārši aprēķiniet to lauku skaitu, kas dos jums uzvaru, un daliet to ar kopējo lauku skaitu.
Piemēram:
- Krāsa - 18/37
- Sudā/Lichá - 18/37
- Ducis - 12/37
- Numurs 0 - 1/37
- Melns un pāra skaitlis - 9/37 (spēles laukā ir tikai 9 skaitļi, kas ir gan melni, gan pāri).
- Ducis un sleja - 4/37 (ir tikai 4 skaitļi ducī un slejā)
Tāpat kā laimesta varbūtību, varat aprēķināt arī zaudējuma varbūtību. Vienkārši saskaitiet to lauku skaitu, kuros nav uzvarētāju, un vēlreiz daliet tos ar kopējo lauku skaitu. Piemēram, likmju uz sarkano likmi varbūtība ir 19/37 (18 melnie lauki + zaļā nulle).
📌 Piezīme: Lai samazinātu daļu līdz 1/x, vienkārši daliet skaitītāju un saucēju ar skaitītāju. Piemēram, 18/37 (abus skaitļus daliet ar 18) pēc korekcijas būs 1/2,055. Tas nozīmē, ka ik pēc 2,055 pagriezieniem viens pagrieziens būs sarkans vai melns.
Vairāku griezienu varbūtība
Kad esat apguvis aprēķinus atsevišķiem griezieniem, ir ļoti vienkārši aprēķināt varbūtību vairākiem griezieniem. Vienkārši reiziniet atsevišķās daļas vienu ar otru.
Piemēri:
- griešanās - likme uz sarkano = 18/37
- griešanās - likme uz duci = 12/37
Uzvaras varbūtība abās kārtās = (18/37)*(12/37)=1/6,34 jeb 15,77% jeb 5,34 pret 1.
- griešanās - tiešā likme - 1/37
- griešanās - tiešā likme - 1/37
Uzvaras varbūtība abās kārtās = (1/37)*(1*37)=1/1369 jeb 0,073% jeb 1368 pret 1.
- griešanās - likme uz melno un nepāra 9/37
- griešanās - likme uz vienādu 18/37
- griešanās - kolonnas likme 12/37
Iespēja uzvarēt visās 3 kārtās = (9/37)*(18/37)*(12/37)=1/26,06 jeb 3,84% jeb 25,06 pret 1. Faktiskā konvertēšana starp ierakstiem atkal ir ļoti vienkārša. Procentus iegūst, dalot daļu formā 1/x un pēc tam reizinot ar 100. Proporcionālo pierakstu formā X līdz 1 iegūsiet, no saucēja atņemot 1, kas ir kopsummas uzvarētāja kārta. Skatīt piemērus virs rindkopas.
Dice varbūtība
Vēl viena azartspēle, kurā ir salīdzinoši viegli aprēķināt izredzes. Pirms mēs sākam aprēķināt laimesta izredzes craps spēlē, aplūkosim pašu kauliņu mešanas varbūtību.
Kaulei ir 6 malas. Tādējādi iespēja, ka jebkurš skaitlis kritīs, ir 1/6. Tradicionāli craps tiek spēlēti ar diviem kauliņiem. Tādējādi divu skaitļu kombinācijas izredzes ir 2/36. Tomēr mūs interesē ne tik daudz konkrēti skaitļi, cik šo skaitļu summa, kas craps spēlē ir daudz svarīgāka. Atkal izmantosim formulu: laimējušo kombināciju skaits/visu kombināciju skaits.
Pieņemsim, ka vēlamies uzzināt varbūtību, ka summa ir 7. Uzvarētāju kombinācijas: (1-6), (2-4), (3-3), (4-2), (6-1). Kā redzat, kopā ir 6 dažādas kombinācijas, kurās uz diviem kauliņiem var izspēlēt summu 7. Tā kā visu kombināciju skaits ir 36, tad 7 kombināciju varbūtība ir 6/36=0,1666.
Šādā veidā var viegli aprēķināt visus citus iespējamos rezultātus.
|
Kopā |
Iespējamība |
|
2 |
1/36 |
|
3 |
2/36 |
|
4 |
3/36 |
|
5 |
4/36 |
|
6 |
5/36 |
|
7 |
6/36 |
|
8 |
5/36 |
|
9 |
4/36 |
|
10 |
3/36 |
|
11 |
2/36 |
|
12 |
1/36 |
Izredzes uzvarēt craps
Īsumā aplūkosim kauliņu noteikumus. Visbiežāk izmantotā likme ir Pass Line.
- Ja jums ir 7 vai 11, jūs vinnēsiet.
- Ja jums ir 2, 3 vai 12, jūs zaudējat.
- Citos gadījumos (4, 5, 6, 8, 9 vai 10) tiek noteikts punkts, kas tiek mests, līdz šis punkts tiek mests vēlreiz (uzvara) vai tiek mests 7 (zaudējums).
Pirms punkta noteikšanas mēs vispirms aprēķinām uzvaras varbūtību. Iespēja trāpīt 7 ir 6/36, bet iespēja trāpīt 11 ir 2/36. Tad šīs divas daļas jāsaskaita kopā, lai iegūtu 3/36+2/36 = 2/9 = 0,2222.
Tagad pievērsīsimies situācijai, kad ir noteikts punkts. Tas ir, ja punkts ir 4, 5, 6, 8, 9 vai 10. Sāksim ar 4.
Ja tiek uzlikta 4, tiek noteikts punkts, un spēlētājs met, līdz tiek uzlikta 4 vai 7. Šeit mēs nonākam nosacītās varbūtības sfērā. Tas norāda, kāda ir notikuma A varbūtība, ja vienlaikus notiek notikums B. Mūsu gadījumā tā būs varbūtība, ka mēs uzvarēsim (velk 4), ja raunds beigsies (velk 4 vai 7). Pēc tam šīs vērtības ierakstām formulā:
- P(A) = Falls summa no 4: 3/36
- P(A∩B) = pēc korekcijām konstatējam, ka tas ir vienāds ar A
- P(B) = izkrīt 4 vai 7: 3/36 + 6/36 = 9/36
No tā izriet, ka:
- P(4|4 vai 7) = (3/36)/(9/36) = 1/3
Līdzīgā veidā varam aprēķināt 5, 6, 8, 9 un 10 summas.
- P(5|5 vai 7) = (4/36)/(10/36) = 2/5
- P(6|6 vai 7) = (5/36)/(11/36) = 5/11
- P(8|8 vai 7) = (5/36)/(11/36) = 5/11
- P(9|9 vai 7) = (4/36)/(10/36) = 2/5
- P(10|10 vai 7) = (3/36)/(9/36) = 1/3
Tagad mēs varam aprēķināt laimesta izredzes kā sākotnējā metiena, kad tika noteikts punkts, un nākamā metiena, kad spēlētājs uzvarēja, varbūtību.
- Sākotnējais metiens 4 x P(4|4 vai 7) = 3/36 x 1/3 = 1/36
- Sākotnējais metiens 5 x P(5|5 vai 7) = 4/36 x 2/5 = 2/45
- Sākotnējais metiens 6 x P(6|6 vai 7) = 5/36 x 5/11 = 25/396
- Sākotnējais metiens 8 x P(8|8 vai 7) = 5/36 x 5/11 = 25/396
- Sākotnējais metiens 9 x P(9|9 vai 7) = 4/36 x 2/5 = 2/45
- Sākotnējais metiens 10 x P(10|10 vai 7) = 3/36 x 1/3 = 1/36
Visas šīs daļskaitļi norāda, cik liela ir varbūtība laimēt, ja pirmais metiens ir 4, 5, 6, 8, 9 vai 10. Ja vēlaties noskaidrot kopējo laimesta varbūtību Pass līnijas likmei, jums ir jāsaskaita tās visas un jāpieskaita iespēja laimēt pirms punkta (metot 7 vai 11 - 2/9).
2/9 + 1/36 + 2/45 + 25/396 + 25/396 + 2/45 + 1/36 = 244/495
Jo 244/495 ir tieši 49,3%. Tas ir nedaudz mazāk par 50 %. Patiesībā jūs, iespējams, neatradīsiet labākas izredzes laimēt ar vinnestu 1 pret 1. Izņemot, iespējams, nūju, ja protat skaitīt kārtis.
Blekdžeka varbūtība
Blekdžeks ir azartspēle, kurā izredzēm ir vislielākā nozīme. Blekdžeka spēlē ar savām prasmēm un zināšanām jūs varat ietekmēt kazino priekšrocības. Jums tikai jāzina optimālā stratēģija, un, ja jūs zināt, kā skaitīt kārtis, jūs pat spēlēsiet ar spēlētāja priekšrocību. Apkārt un ap jums patiesībā nav jāzina visas konkrētās varbūtības, jo visus šos aprēķinus jau ir veikuši matemātiķi pirms jums, kuri izstrādāja visas blackjack taktikas un stratēģijas.
Tomēr interesantības labad mēs parādīsim, kā aprēķināt dažu svarīgu blackjack parādību varbūtību.
Ja uz varbūtības problēmu raugāmies no kāršu komplekta perspektīvas, ir skaidrs, ka iespējamo iznākumu skaits strauji palielinās. Blekdžeku spēlē ar 52 kāršu komplektu, kurā ir 4 krāsas un 13 vērtības. Tas dod šādas izredzes:
- Es izlozēju dūzi no kāršu komplekta (vai jebkuru citu kārti): 4/52=0,0769 (7,69%).
- Es izlozēju no kārbas pīķi: 13/52=0,25 (25%).
Tomēr atšķirībā, piemēram, no monētas metiena, ruletes vai spēļu automātiem, kāršu dēlim ir sava veida "atmiņa". Vai drīzāk tas nozīmē, ka iepriekšējie rezultāti ietekmē pašreizējos un turpmākos gājienus. Tas ir saistīts ar to, ka no kāršu komplekta ir izņemta karte, un tas maina sākuma situāciju. Aplūkosim piemēru, kad pirmā kārts, kas izlozēta no 52 kāršu komplekta, ir dūzs (7,69% iespēja). Varbūtība, ka kā otrā kārts no komplekta tiks izvilkts dūzs, tagad būs atšķirīga. Pēc pirmās izspēles dūžu skaits ir samazinājies līdz 3, bet kāršu skaits - līdz 51.
Varbūtība blackjack dabas
Vispirms ikvienu spēlētāju interesēs nūju varbūtība. Tas ir, kādas ir izredzes, ka spēlētājam uzreiz raunda sākumā būs dūzis un desmit kārtis - citiem vārdiem sakot, dabiska kārts.
Šāda situācija var rasties divējādi, un, tos saskaitot, mēs iegūstam mūsu izredzes uz nūju:
📌 Piezīme: mēs skaitām vienpakāpes nūju. Tātad 52 kartes, 4 dūži un 16 desmitnieki. Dīlera karte nav redzama, tāpēc tā neietekmē varbūtību.
- Spēlētājs saņem pirmo dūzi un desmit kārtis.
Spēlētājam tiek izdalīta pirmā dūža kārts ar varbūtību 4/52. Tātad spēlētājam ir jāsaņem otrā kārts ar desmitnieku, un šim nolūkam koeficients ir 16/51. Šīs divas varbūtības ir jāreizina viena ar otru, lai iegūtu 16/663.
- Spēlētājs saņem pirmo desmit kārtis un dūzi.
Varbūtība, ka spēlētājs saņems pirmo kārti ar vērtību 10, ir 16/52. Izredzes, ka spēlētājs pēc tam saņems dūzi, ir 4/51. Pēc reizināšanas iegūstam 16/663.
Ja vēlamies noskaidrot, cik liela ir varbūtība, ka mums izdosies vinnests, mēs vienkārši saskaitām šīs divas parādības. Tātad 16/663 + 16/663 = 32/663 = 4,827%. Citiem vārdiem sakot, spēlētājs "blackjack" gūst aptuveni reizi 20 izspēlēs. Līdzīgā veidā var aprēķināt varbūtību arī vairāku klāju galdiem, ko mēs jau esam izdarījuši.
|
Iepakojumu skaits |
Iespējamība |
|
1 |
4,827 % |
|
2 |
4,780 % |
|
3 |
4,764 % |
|
4 |
4,757 % |
|
5 |
4,752 % |
|
6 |
4,749 % |
Sprādziena varbūtība
Tāpat varētu būt interesanti uzzināt, kādas ir jūsu izredzes tikt izslēgtam. Arī šajā gadījumā mēs pievērsīsimies situācijas paraugam, kad Jūs spēlējat tikai ar dīleri pie viena kāršu galda. Aplūkosim ļoti vienkāršu situāciju, kad spēlētājam ir 2 kartes ar kopējo vērtību 10, tātad viņam ir 20 punkti. Situācijā, kad spēlētājs saņem trešo kārti, no komplekta jau ir izspēlētas 3 kārtis. Tādējādi kāršu komplektā paliek 49 kārtis. No šīm 49 kārtīm jums palīdzēs tikai 4 dūži. No šīm 49 kartēm 45 ir nevēlamas. Tāpēc izredzes uz bankrotu ir 45/49=0,9183673.
Līdzīgi var aprēķināt arī citas varbūtības. Jums vienmēr ir jāspēj pareizi iztēloties situāciju. Tas ir viss.
|
Rokas vērtība |
Pārrāvumu iespējamība |
|
21 |
100 % |
|
20 |
92 % |
|
19 |
85 % |
|
18 |
77 % |
|
17 |
69 % |
|
16 |
62 % |
|
15 |
58 % |
|
14 |
56 % |
|
13 |
39 % |
|
12 |
31 % |
|
11 mazāk |
0 % |
Tālāk aplūkosim, cik liela ir varbūtība, ka dīleris atmaksās katru kārti.
|
Rokas vērtība |
Pārrāvumu iespējamība |
|
2 |
35,30 % |
|
3 |
37,56 % |
|
4 |
40,28 % |
|
5 |
42,89 % |
|
6 |
42,08 % |
|
7 |
25,99 % |
|
8 |
23,86 % |
|
9 |
23,34 % |
|
10, J, Q, K |
21,43 % |
|
Dūzis |
11,65 % |
Pokera varbūtība
Pokers ir vēl viena kāršu spēle, kurā varbūtība ir ļoti svarīga. Cita starpā. Apskatīsim, kādas ir jūsu izredzes spēlēt pokeru.
Pre-flop varbūtība
Tagad, kad esam izklāstījuši, kā varbūtība darbojas kāršu depozītā, pievērsīsimies praktiskiem pielietojumiem. Vispirms mēs parādīsim, kā aprēķināt varbūtību, ka izspēlē beigsies pāri. (piemēram, daudz apspriestie "Aces"). Šajā gadījumā mums ir jāreizina varbūtības viena ar otru.
(4/52) x (3/51) = (12/2652) = (1/221) = 0,004524 (0,45 %)
📌 Piezīme: ja Jūs spēlējat pokeru kazino, kur tiek izspēlētas aptuveni 30 izspēles stundā, Jūs dabūsiet dūžu pāri aptuveni reizi septiņās ar pusi spēles stundās.
Kādas ir izredzes iegūt kādu no 13 iespējamajiem pāriem, kad veicat izlozi? Varam pieņemt, ka izredzes ir 1/221 katram pārim (sk. formulu iepriekš). Kopumā var būt 13 šādi pāri, tāpēc aprēķina formula būs 13/221=0,0588. Tātad jūs varat sagaidīt, ka pāris tiks izspēlēts aptuveni reizi 35 spēlēs.
Iespējamība pokerā spēlētājs pret spēlētāju
Tomēr pokers ir vairāku spēlētāju spēle, ko parasti spēlē viens pret otru. Šeit ir aprakstītas visbiežāk sastopamās pre-flop situācijas.
|
Jūsu roka |
Jūsu pretinieka roka |
Uzvaras varbūtība |
|
Augsts pāris |
Divas zemas kartes |
83 % |
|
Augsts pāris |
Zems pāris |
82 % |
|
Vidējais pāris |
Augsta, zema karte |
71 % |
|
Divas augstas kārtis |
Divas zemas kartes |
63 % |
|
Divas augstas kārtis |
Zems pāris |
55 % |
Varbūtības aprēķināšana pēc "outs"
Ja Jums izdosies ieraudzīt kārtis uz flopa, Jūs noteikti vēl vairāk interesēs, kādas ir Jūsu izredzes uzlabot savu kombināciju. Šajā gadījumā mēs runāsim par tā sauktajiem "ārējiem". Pokera spēlē šis termins attiecas uz jebkurām kārtīm, kas var Jums palīdzēt. Šāds biežs gadījums var būt, kad spēlētājam ir divas vienas krāsas kārtis un uz flopa parādās vēl divas tādas pašas krāsas kārtis. Pēc tam spēlētājam ir 4 kārtis, ar kurām viņš var izveidot "flush", un tādējādi viņam ir 9 "out" kārtis, tātad 9 kārtis, ar kurām var izveidot "flush".
|
Izslēgšanas gadījumu skaits |
Flop - Turn |
Pagrieziens - River |
Pagrieziet upi |
|
20 |
42,6 % |
43,5 % |
67,5 % |
|
19 |
40,4 % |
41,3 % |
65,0 % |
|
18 |
38,3 % |
39,1 % |
62,4 % |
|
17 |
36,2 % |
37,0 % |
59,8 % |
|
16 |
34,0 % |
34,8 % |
57,0 % |
|
15 |
31,9 % |
32,6 % |
54,1 % |
|
14 |
29,8 % |
30,4 % |
51,2 % |
|
13 |
27,7 % |
28,3 % |
48,1 % |
|
12 |
25,5 % |
26,1 % |
45,0 % |
|
11 |
23,4 % |
23,9 % |
41,7 % |
|
10 |
21,3 % |
21,7 % |
38,4 % |
|
9 |
19,1 % |
19,6 % |
35,0 % |
|
8 |
17,0 % |
17,4 % |
31,5 % |
|
7 |
14,9 % |
15,2 % |
27,8 % |
|
6 |
12,8 % |
13,0 % |
24,1 % |
|
5 |
10,6 % |
10,9 % |
20,3 % |
|
4 |
8,5 % |
8,7 % |
16,5 % |
|
3 |
6,4 % |
6,5 % |
12,5 % |
|
2 |
4,3 % |
4,3 % |
8,4 % |
|
1 |
2,1 % |
2,2 % |
4,3 % |
📌 Piezīme: ir ļoti vienkārša metode, kā aprēķināt "outs" varbūtību, lai to varētu izdarīt turpat pie galda. To parasti sauc par "četri un divi" noteikumu. Pēc flopa spēlētājs vienkārši reizina "outs" skaitu ar 4, lai noteiktu turna un rivera varbūtību. Ja viņš nesaņem kārti turnā, viņš vienkārši reizina izkritušo kāršu skaitu ar divi, lai iegūtu aptuveno varbūtību, ka viņš saņems kārti uz rivera.
Atkal mēs varam izmantot piemēru, kad pēc flopa mums ir 4 vienas krāsas kārtis. Tātad Jūsu "out" ir 9 kārtis, un pēc kāršu kārtas un rivera kāršu kārtošanas varbūtība ir 36% (9x4). Pieņemsim, ka kārtas laikā jūs nesaņemat karti. Šajā gadījumā mēs reizinām izkritušās kārtis ar divi un iegūstam, ka mums ir 18% (9x2) iespēja, ka uz rivera beigsies šīs krāsas kārtis. Kā redzat, salīdzinot tabulu, šī metode ir ļoti vienkārša, bet, no otras puses, neprecīza, taču to var izmantot.

 LV
LV  English
English  čeština
čeština  Polski
Polski  Slovenčina
Slovenčina  Русский
Русский  Deutsch
Deutsch  Slovenski
Slovenski  Dutch
Dutch  Svenska
Svenska  Português
Português  Italiano
Italiano  Español
Español  Français
Français  Suomalainen
Suomalainen  Български
Български  Românesc
Românesc  Magyar
Magyar  Eesti
Eesti  Ελληνική
Ελληνική  Lietuvių
Lietuvių  やまと
やまと  中国
中国  Dansk
Dansk  Türkçe
Türkçe  ID
ID  Українська
Українська  한국어
한국어  Norsk
Norsk 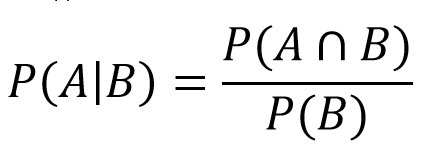


Lai pievienotu komentāru, jums ir jābūt piereģistrētam.