Do you understand the probability of casino games? If you are going to play at a casino, you should make sure you know your chances and understand them perfectly. Why? Because probability is the engine that makes casinos work. Without probability, the gambling industry would not be possible.
Chance is simply the probability that something will happen. Probability is part of our everyday life. When we decide to cross a busy street at a red light, there is a certain chance that we will be hit by a car, but in return, we have a chance to cross the street faster and gain some time to spare.
When we gamble, we estimate the probability of a certain event happening in order to formulate our bet. It is in these cases that we calculate probability.
💡Probability example
Let's say we have a bag containing four balls of which the only one is red and the other three are blue. The probability of pulling out just the red ball without looking is 1 in 4.
There are several ways to express probability. We can also say that there is a 3 in 1 chance against red because on average we draw three blue balls for every red ball drawn.
We can also express our chances as a percentage, so our probability of drawing a red ball is 25% if there is a 100% chance of drawing a ball. So 100 divided by four gives us 25%.
The probability of drawing a blue ball is 75% if there are three blue balls with a 25% chance of drawing.
The casino operates on the principle of offering odds that are not that good considering our long-term result.
The example of a bag of balloons is a simple way to show how a casino works. Let's say a casino offers odds of 3 to draw a red ball. If you bet $5, then on average, in four attempts you will pull your blue ball 3 times and lose $15, and on the fourth time you pull your red ball and win $10, but the casino will still be in the black by $5
All gambling is about probability. Any experienced gambler will tell you that. It is therefore essential to know and work with these numbers. So here we will now show you how to calculate the probability in gambling. If you understand the principle correctly, you can use it to calculate the probability of anything else.
Roulette is like the Wheel of Fortune. And you know why? It only takes 3 words to explain - Big Number Theory. Every person who runs a casino or produces online casino games knows this theory very well. Because it is directly linked to his earnings. And thanks to it, the casino always wins over the bettors in the long run too. Everything is linked to probability and the house edge.
📌 Note: All numbers in the article refer to European Roulette - so we count 37 numbers.
There are several ways to write probability. Probably the best known is percentages. In addition to these, expressions using a fraction or a ratio are used.
📌 Note: As big number theory says, the probability is essentially a mathematical limit. With more and more trials, you realistically get closer and closer to the calculated result.
As you can see, the expressions using fractions and using ratios are very similar. The only difference is that a fraction counts all spins, while a ratio splits the total spins into two categories.
Table of probabilities for individual bets in roulette
| Bet | Odds | Ratio | Probability |
| Even Bet | 1/2,055 | 1,055 to 1 | 48,6% |
| Column | 1/3,08 | 2,08 to 1 | 32,4% |
| Dozen | 1/3,08 | 2,08 to 1 | 32,4% |
| Six Line | 1/6,17 | 5,17 to 1 | 16,2% |
| Roh | 1/9,25 | 8,25 to 1 | 10,8% |
| Street | 1/12,33 | 11,33 to 1 | 8,1% |
| Split | 1/19,5 | 18,5 to 1 | 5,4% |
| Straight | 1/37 | 36 to 1 | 2,7% |
A mathematical comparison for the repetition of the selected phenomenon could also be interesting. For this case, we have chosen a straight bet, specifically for example a bet on red. So, what will be the changing probability of red 5 times in a row, for example?
| Number of spins | Odds | Probability |
| 1 | 1,06 to 1 | 48,6 % |
| 2 | 3,23 to 1 | 23,7 % |
| 3 | 7,69 to 1 | 11,5 % |
| 4 | 16,9 to 1 | 5,6 % |
| 5 | 35,7 to 1 | 2,73 % |
| 6 | 74,4 to 1 | 1,33 % |
| 7 | 154 to 1 | 0,65 % |
| 8 | 318 to 1 | 0,31 % |
| 9 | 654 to 1 | 0,15 % |
| 10 | 1 346 to 1 | 0,074 % |
| 15 | 49 423 to 1 | 0,002 % |
| 20 | 1 813 778 to 1 | 0,000055 % |
As can be seen, as the number of spins increases, the probability of this phenomenon decreases rapidly. However, keep in mind that these probabilities describe the phenomenon as a whole. The random number generator does not take into account previous outcomes, so even though a game series where red hits 20 times in a row occurs once every 1.813 million games, a 21 game round will have the same house edge and probability (i.e. 48.6%) as every other game round.
Often, in this case, one can encounter the term Player's Fallacy, where the bettor believes that if one colour is hit several times in a row, there is a higher probability that the other colour will be hit in the next spin. In reality, this is not the case. The most famous case of this fallacy was observed in 1913 at the Monte Carlo Casino, when black fell 26 times in a row on the roulette wheel, and for almost the entirety of this incredible streak, and even after it ended, people bet frenetically on red. That's when the casino made some very nice money.
📌 Note: The probability of a color being hit 26 times in a row is 0.000000730870% and occurs once in 67 million games.
Want to know more odds for individual bets? Try calculating them yourself. Working with percentages and probabilities is not very complicated. Generally, the easiest way is to start with fractions and use them to calculate further percentages and ratios. For example, if you want to calculate the probability in a fraction for a situation where the red is red, you do the following:
Total number of reds on the playing field/Total number of playing fields = 18/37
Again, a simple rule applies here. Simply calculate the number of fields that will give you a win and divide it by the total number of fields.
For example:
Just like the probability of winning, you can calculate the probability of losing. Just count the number of non-winning fields and divide them again by the total number of fields. For example, the probability of losing if you bet on red is 19/37 (18 black fields + green zero).
📌 Note: To reduce a fraction to 1/x, simply divide the numerator and denominator by the numerator. For example, 18/37 (you divide both numbers by 18) will be 1/2.055 after the adjustment. And so this means that for every 2.055 turns, one turn will result in a red or a black.
Once you have mastered the calculation for single spins, calculating the probability for multiple spins is very simple. Just multiply the individual fractions by each other.
Examples:
Probability of winning both rounds = (18/37)*(12/37)=1/6.34 or 15.77% or 5.34 to 1
Probability of winning both rounds = (1/37)*(1*37)=1/1369 or 0.073% or 1368 to 1
Probability of winning all 3 rounds = (9/37)*(18/37)*(12/37)=1/26.06 or 3.84% or 25.06 to 1
Again, the conversion between entries is very easy. You get the percentages by dividing the fraction in the form 1/x and then multiplying by 100. You get the ratio notation in the form of X to 1 by subtracting 1 from the denominator, which is the winning round of the total. See examples above the paragraph.
Craps is another game of chance in which it is relatively easy to calculate the odds. Before we get into calculating the odds of winning at craps, let's take a look at the probability of dice rolls themselves.
The dice have 6 sides. The chance that any number will fall is therefore 1/6. Craps is traditionally played with two dice. The odds of any two numbers combining are therefore 2/36. However, we are not so much interested in the specific numbers as the sum of those numbers, which is much more important in craps. Again, we'll use the formula: number of winning combinations/number of all combinations.
Let's say we want to know the probability for the sum of 7. Winning combinations: (1-6), (2-4), (3-3), (4-2), (6-1). As you can see, there are a total of 6 different combinations where the sum of 7 can be rolled on two dice. And since the number of all combinations is 36, the probability of 7 is 6/36=0.1666
In this way, all other possible results can be easily calculated.
| Sum | Probability |
| 2 | 1/36 |
| 3 | 2/36 |
| 4 | 3/36 |
| 5 | 4/36 |
| 6 | 5/36 |
| 7 | 6/36 |
| 8 | 5/36 |
| 9 | 4/36 |
| 10 | 3/36 |
| 11 | 2/36 |
| 12 | 1/36 |
Briefly, let's take a look at the dice rules. The most common bet is the Pass Line.
We first calculate the probability of winning before determining the point. The chance of hitting 7 is 6/36 and the chance of hitting 11 is 2/36. These two fractions must then be added together to give 3/36+2/36 = 2/9 = 0.2222.
We now turn our attention to the situation where a point is determined. That is when the point is 4, 5, 6, 8, 9 or 10. Let's start with a total of 4.
If a 4 is rolled, a point is determined and the player rolls until a 4 or 7 is rolled. This is where we enter the realm of conditional probability. This tells us what the probability of event A is if event B occurs at the same time. In our case, it will be the probability that we win (rolls a 4) if the round ends (rolls a 4 or a 7). We then plug these values into the formula:
It follows that:
In a similar way we can calculate the sums of 5, 6, 8, 9 and 10
Now we can calculate the chance of winning as the probability of the original roll when the point was determined and the next roll when the player won.
All these fractions give us the probability of winning if the first roll is 4, 5, 6, 8, 9 or 10. If you want to know the total probability of winning on a Pass line bet, you need to add them all up and add the chance of winning before the point (rolls a 7 or 11 - 2/9).
2/9 + 1/36 + 2/45 + 25/396 + 25/396 + 2/45 + 1/36 = 244/495
Because 244/495 is exactly 49.3%. That's just under 50%. In fact, you probably won't find a better chance of winning with a 1 in 1 payout. Except maybe blackjack, if you can count cards.
Blackjack is the game of chance in which the odds matter most. In blackjack, you can influence the house edge with your skill and knowledge. You just need to know the optimal strategy for this, and if you know how to count cards, you will even play with the player's advantage. Around and around you don't actually need to know all the specific probabilities, because all these calculations have already been done by mathematicians before you who came up with all the tactics and strategies for blackjack.
However, for the sake of interest, we will show how to calculate the probability for some important phenomena in blackjack.
If we look at the problem of probability from the perspective of a deck of cards, it is clear that the number of possible outcomes increases rapidly. Blackjack is played with a deck of 52 cards, 4 suits and 13 values. This gives the following odds:
However, unlike a coin toss, roulette or slot machines, for example, a deck of cards has something of a "memory". Or rather, it means that previous results have an effect on current and future moves. This is due to the fact that a card has been dropped from the deck and this changes the starting situation. Let's look at an example where the first card drawn from a 52-card deck was an Ace (7.69% chance). The probability that an Ace will be drawn again as the second card from the deck will now be different. After the first draw, the number of aces has dropped to 3 and the number of cards to 51.
What every player will be interested in first is the probability of blackjack. That is, what are the chances that a player will get an ace and a ten card right at the start of the round - in other words, a natural.
This situation can occur in two ways, and if we add the two ways, we get our odds on blackjack:
📌 Note: We are counting for single deck blackjack. So 52 cards, 4 aces and 16 tens. The dealer's card is not visible, so it will not affect the probability.
The player is dealt the first Ace card with a probability of 4/52. So the player must get the second card with a ten, and for that, the odds are 16/51. These two probabilities must be multiplied by each other to get 16/663.
The probability that a player will receive the first card with a value of 10 is 16/52. The odds of a player getting an Ace after that are 4/51. After multiplying, we get 16/663.
If we want to know the probability of getting a blackjack we just add these two phenomena. So 16/663 + 16/663 = 32/663 = 4.827%. In other words, a player gets a blackjack about once every 20 hands. You can calculate the probability for multi-deck tables in a similar way, which we have already done for you.
| Number of decks | Probability |
| 1 | 4,827 % |
| 2 | 4,780 % |
| 3 | 4,764 % |
| 4 | 4,757 % |
| 5 | 4,752 % |
| 6 | 4,749 % |
It might also be interesting to know what your odds are for a bust. Again, we'll focus on a sample situation where you're playing with just the dealer at a single deck table. Let's take a look at a very simple situation where a player has 2 cards with a value of 10 in total so he has 20 points. In a situation where the player gets a third card, 3 cards have already been played from the deck. This leaves 49 cards in the deck. Of these 49 cards, only 4 aces will help you. Of these 49, 45 cards are unwanted. Therefore, the odds of a bust are 45/49=0.9183673.
You can calculate other probabilities in a similar way. You always have to be able to imagine the situation correctly. That's all.
| Hand combination | Probability of bust |
| 21 | 100 % |
| 20 | 92 % |
| 19 | 85 % |
| 18 | 77 % |
| 17 | 69 % |
| 16 | 62 % |
| 15 | 58 % |
| 14 | 56 % |
| 13 | 39 % |
| 12 | 31 % |
| 11 méně | 0 % |
Let's next look at how likely the dealer will bust for each card.
| Hand combination | Probability of bust |
| 2 | 35,30 % |
| 3 | 37,56 % |
| 4 | 40,28 % |
| 5 | 42,89 % |
| 6 | 42,08 % |
| 7 | 25,99 % |
| 8 | 23,86 % |
| 9 | 23,34 % |
| 10, J, Q, K | 21,43 % |
| Eso | 11,65 % |
Poker is another card game where probability is extremely important. Among other things. So let's take a look at what your chances are at poker.
Now that we've outlined how probability works in a deck of cards, let's get down to practical applications. First of all, we'll show how to calculate the probability of running out of pairs in a hand. (for example, the much talked about Aces). In this case, we need to multiply the probabilities by each other.
(4/52) x (3/51) = (12/2652) = (1/221) = 0,004524 (0,45 %)
📌 Note: If you play poker in a casino that deals about 30 hands per hour, you will get a pair of aces about once every 7 and a half hours of play.
So what are the chances of getting any of the 13 possible pairs when you deal? We can assume that the odds are 1/221 per individual pair (see formula above). There can be 13 of these pairs in total, so the formula for the calculation will be 13/221=0.0588. So you can expect a pair about once every 35 games.
However, poker is a multiplayer game, usually played against each other. So here is a selection of the most common pre-flop situations.
| Your hand | Other player's hand | Probability of winning |
| High pair | Two low card | 83 % |
| High pair | Low pair | 82 % |
| Middle pair | High card, low card | 71 % |
| Two high cards | Two low cards | 63 % |
| Two high cards | Low pair | 55 % |
If you manage to see the cards on the flop, you will certainly be further interested in what your chances are of improving your hand. In this case, we will talk about the so-called "outs". In poker, this term refers to any cards that can help you. Such a common case can be when a player holds two cards in a suit and two more cards of the same suit appear on the flop. The player then has 4 cards to flush and thus has 9 outs, leaving 9 cards with which to form a flush.
| Number of outs | Flop - Turn | Turn - River | Turn a River |
| 20 | 42,6 % | 43,5 % | 67,5 % |
| 19 | 40,4 % | 41,3 % | 65,0 % |
| 18 | 38,3 % | 39,1 % | 62,4 % |
| 17 | 36,2 % | 37,0 % | 59,8 % |
| 16 | 34,0 % | 34,8 % | 57,0 % |
| 15 | 31,9 % | 32,6 % | 54,1 % |
| 14 | 29,8 % | 30,4 % | 51,2 % |
| 13 | 27,7 % | 28,3 % | 48,1 % |
| 12 | 25,5 % | 26,1 % | 45,0 % |
| 11 | 23,4 % | 23,9 % | 41,7 % |
| 10 | 21,3 % | 21,7 % | 38,4 % |
| 9 | 19,1 % | 19,6 % | 35,0 % |
| 8 | 17,0 % | 17,4 % | 31,5 % |
| 7 | 14,9 % | 15,2 % | 27,8 % |
| 6 | 12,8 % | 13,0 % | 24,1 % |
| 5 | 10,6 % | 10,9 % | 20,3 % |
| 4 | 8,5 % | 8,7 % | 16,5 % |
| 3 | 6,4 % | 6,5 % | 12,5 % |
| 2 | 4,3 % | 4,3 % | 8,4 % |
| 1 | 2,1 % | 2,2 % | 4,3 % |
📌 Note: There is a very easy method for calculating the probability of outs, so you can do it right at the table. It is generally called the "four and two" rule. After the flop, the player simply multiplies the number of outs by 4 to find the probability for the turn and river. If he doesn't get the card on the turn, he simply multiplies the number of outs by two to get the approximate probability of getting the card on the river.
Again, we can use the example of having 4 cards of the same suit after the flop. So your outs are 9 cards and the probability of a flush after the turn and river is 36% (9x4). Let's say you don't get a card on the turn. In that case, we then multiply the outs by two and find that we have an 18% (9x2) chance of running out of cards in the suit on the river. As you can see by comparing the table, this method is really simple but on the other hand inaccurate, but it can be used.
EN 
čeština
Polski
Slovenčina
Русский
Deutsch
Slovenski
Dutch
Svenska
Português
Italiano
Español
Français
Suomalainen
Български
Românesc
Magyar
Eesti
Ελληνική
Latviešu
Lietuvių
やまと
中国
Dansk
Українська
Norsk
Peter Sommer 
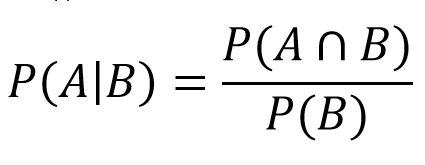
You have to be logged in to add a comment