Olasılık ve kumarhane oyunları
 Peter Sommer
Peter Sommer
Şansınızın farkında mısınız? Bir kumarhanede oynayacaksanız, şansınızı bildiğinizden ve onları mükemmel bir şekilde anladığınızdan emin olmalısınız. Neden? Çünkü kumarhanelerin çalışmasını sağlayan motor olasılıktır. Olasılık olmadan kumar endüstrisi mümkün olmazdı.
Şans, basitçe bir şeyin gerçekleşme olasılığıdır. Olasılık günlük hayatımızın bir parçasıdır. Kırmızı ışıkta işlek bir caddede karşıdan karşıya geçmeye karar verdiğimizde, bize bir arabanın çarpma ihtimali vardır, ancak bunun karşılığında karşıdan karşıya daha hızlı geçme ve biraz zaman kazanma şansımız vardır.
Kumar oynarken, bahsimizi formüle etmek için belirli bir olayın gerçekleşme olasılığını tahmin ederiz. İşte bu durumlarda olasılığı hesaplarız.
💡 Olasılık örneği
Diyelim ki, içinde sadece biri kırmızı ve diğer üçü mavi olmak üzere dört top bulunan bir torbamız var. Bakmadan sadece kırmızı topu çekme olasılığı 4'te 1'dir.
Olasılığı ifade etmenin çeşitli yolları vardır. Kırmızıya karşı 3'te 1 şans olduğunu da söyleyebiliriz, çünkü ortalama olarak çekilen her kırmızı top için üç mavi top çekeriz.
Şansımızı yüzde olarak da ifade edebiliriz, yani bir top çekme şansımız %100 ise kırmızı top çekme olasılığımız %25'tir. Yani 100 bölü dört bize %25 verir.
Çekme şansı %25 olan üç mavi top varsa mavi top çekme olasılığı %75'tir.
Casino oyunlarının olasılığı
Kumarhane, uzun vadeli sonucumuz göz önüne alındığında o kadar da iyi olmayan oranlar sunma prensibiyle çalışır.
Bir torba balon örneği, bir kumarhanenin nasıl çalıştığını göstermenin basit bir yoludur. Diyelim ki bir kumarhane kırmızı top çekmek için 3 oran sunuyor. Eğer 5 dolar yatırırsanız, ortalama olarak, dört denemede mavi topunuzu 3 kez çekecek ve 15 dolar kaybedeceksiniz ve dördüncü seferde kırmızı topunuzu çekecek ve 10 dolar kazanacaksınız, ancak kumarhane yine de 5 dolar karda olacak.
Tüm kumar oyunları olasılıkla ilgilidir. Deneyimli
her kumarbaz
size bunu söyleyecektir. Bu nedenle, bu sayılara aşina olmak ve onlarla nasıl çalışılacağını bilmek çok önemlidir. Şimdi burada size kumarda olasılığı nasıl hesaplayacağınızı göstereceğiz. Prensibi doğru anlarsanız, bunu başka herhangi bir şeyin olasılığını hesaplamak için kullanabilirsiniz.
Rulette Olasılık
Rulet, Çarkıfelek gibidir. Neden biliyor musun? Açıklamak için sadece 3 kelime yeterli - Büyük Sayı Teorisi. Bir kumarhane işleten veya çevrimiçi kumarhane oyunları üreten herkes bu teoriyi çok iyi bilir. Çünkü doğrudan kazancıyla bağlantılıdır. Ve bu sayede, kumarhane de uzun vadede her zaman bahisçilere karşı kazanır. Her şey olasılık ve kasa avantajı ile bağlantılıdır.
📌 Not: Makaledeki tüm sayılar Avrupa Ruletine atıfta bulunmaktadır - bu nedenle 37 sayı sayıyoruz.
Olasılık nasıl yazılır
Olasılık yazmanın birkaç yolu vardır. Muhtemelen en iyi bilineni yüzdelerdir. Bunlara ek olarak, kesir veya oran kullanan ifadeler de kullanılır.
- Yüzde (%) olarak ifade edilir - buraya eklenecek fazla bir şey yoktur, ancak sadece eksiksizlik için, bu seçilen olay için yüzdedir. (Parça/Toplam)*100 olarak hesaplanır. Örneğin, bir rulet çarkında seçilen numarayı tutturma olasılığı (Düz): 1/37*100=%2,7
- Kesir kullanarak ifade (1/x) - Olasılığı bir kesir kullanarak ifade ederken, olgunun X denemede 1 kez meydana geldiğini söyleriz. Sayısal ifadede, yüzdelerin hesaplanmasına güveniyoruz. Yukarıdaki 1/37 örneğini ele alırsak, bu, rulet çarkında istatistiksel olarak seçilen bir sayının 37 turda 1 kez düşeceği anlamına gelir.
- Orana göre ifade (x'ten 1'e) - Her X oluştuğunda, seçilen olgu 1 kez gerçekleşir. Burada yine rulette seçilen sayı için olasılığa bağlı kalıyoruz. Bu durumda oran 36'ya 1 olarak yazılacaktır. Bu, sayının düşmediği her 36 döndürmeden sonra, seçilen sayının düştüğü bir örnek olacağı anlamına gelir.
📌 Not: Büyük sayı teorisinin dediği gibi, olasılık esasen matematiksel bir limittir. Giderek daha fazla denemeyle, hesaplanan sonuca gerçekçi bir şekilde daha da yaklaşırsınız.
Gördüğünüz gibi, kesirlerin kullanıldığı ifadeler ile oranların kullanıldığı ifadeler birbirine çok benzemektedir. Tek fark, bir kesir tüm dönüşleri sayarken, bir oran toplam dönüşleri iki kategoriye ayırır.
Rulette bireysel bahisler için olasılıklar tablosu
|
Bahis |
Alıntı |
Oran |
Yüzdeler |
|
Düz bahis |
1/2,055 |
1.055'e 1 |
48,6 % |
|
Sütun |
1/3,08 |
2.08'e 1 |
32,4 % |
|
The Dozen |
1/3,08 |
2.08'e 1 |
32,4 % |
|
Altı Hat |
1/6,17 |
5.17'ye 1 |
16,2 % |
|
Köşe |
1/9,25 |
8.25'e 1 |
10,8 % |
|
Sokak |
1/12,33 |
11.33'e 1 |
8,1 % |
|
Bölünmüş |
1/19,5 |
18.5'e 1 |
5,4 % |
|
Düz |
1/37 |
36'ya 1 |
2,7 % |
Düz bahis için olasılık
Seçilen olgunun tekrarı için matematiksel bir karşılaştırma da ilginç olabilir. Bu durumda düz bir bahis seçtik, özellikle örneğin kırmızı üzerine bir bahis. Peki, örneğin arka arkaya 5 kez kırmızının değişme olasılığı ne olacaktır?
|
Döndürme sayısı |
Oran |
Yüzdeler |
|
1 |
1.06'ya 1 |
48,6 % |
|
2 |
3.23'e 1 |
23,7 % |
|
3 |
7.69'a 1 |
11,5 % |
|
4 |
16.9'a 1 |
5,6 % |
|
5 |
35.7'ye 1 |
2,73 % |
|
6 |
74.4'e 1 |
1,33 % |
|
7 |
154'e 1 |
0,65 % |
|
8 |
318'e 1 |
0,31 % |
|
9 |
654'e 1 |
0,15 % |
|
10 |
1 346'ya 1 |
0,074 % |
|
15 |
49 423'e 1 |
0,002 % |
|
20 |
1 813 778 - 1 |
0,000055 % |
Görüldüğü gibi spin sayısı arttıkça bu olayın gerçekleşme olasılığı hızla azalmaktadır. Ancak, bu olasılıkların olguyu bir bütün olarak tanımladığını unutmayın. Rastgele sayı üreticisi önceki sonuçları dikkate almaz, bu nedenle kırmızının arka arkaya 20 kez vurduğu bir oyun serisi her 1,813 milyon oyunda bir gerçekleşse bile, 21 oyun turu diğer tüm oyun turlarıyla aynı kasa avantajına ve olasılığa (yani %48,6) sahip olacaktır.
Bu durumda genellikle Oyuncu Yanılgısı terimiyle karşılaşılabilir; burada bahisçi, bir renk arka arkaya birkaç kez tutturulursa, bir sonraki dönüşte diğer rengin tutturulma olasılığının daha yüksek olduğuna inanır. Gerçekte durum böyle değildir. Bu yanılgının en ünlü örneği 1913 yılında Monte Carlo Casino'sunda rulet çarkında siyahın 26 kez üst üste düşmesi ve bu inanılmaz serinin neredeyse tamamı boyunca ve hatta bittikten sonra bile insanların çılgınca kırmızıya bahis oynamasıdır. İşte o zaman kumarhane çok iyi para kazandı.
📌 Not: Bir rengin arka arkaya 26 kez vurulma olasılığı %0,000000730870'tir ve 67 milyon oyunda bir kez gerçekleşir.
Rulet olasılığı nasıl hesaplanır
Bireysel bahisler için daha fazla oran öğrenmek ister misiniz? Kendiniz hesaplamayı deneyin. Yüzdeler ve olasılıklarla çalışmak çok karmaşık değildir. Genel olarak en kolay yol kesirlerle başlamak ve bunları daha fazla yüzde ve oran hesaplamak için kullanmaktır. Örneğin, kırmızının kırmızı olduğu bir durum için bir kesirdeki olasılığı hesaplamak istiyorsanız, aşağıdakileri yaparsınız:
Oyun alanındaki toplam kırmızı sayısı/Toplam oyun alanı sayısı = 18/37
Bir spin için olasılık
Burada da yine basit bir kural geçerlidir. Size kazanç sağlayacak alanların sayısını hesaplayın ve toplam alan sayısına bölün.
Örneğin:
- Renk - 18/37
- Sudá/Lichá - 18/37
- Düzine - 12/37
- Sayı 0 - 1/37
- Siyah ve çift - 9/37 (oyun alanında hem siyah hem de çift olan sadece 9 sayı vardır)
- Düzine ve sütun - 4/37 (bir düzinede ve bir sütunda sadece 4 sayı vardır)
Tıpkı kazanma olasılığı gibi, kaybetme olasılığını da hesaplayabilirsiniz. Sadece kazanamayan sahaların sayısını sayın ve tekrar toplam saha sayısına bölün. Örneğin, kırmızı üzerine bahis oynarsanız kaybetme olasılığınız 19/37'dir (18 siyah alan + yeşil sıfır).
📌 Not: Bir kesri 1/x'e indirgemek için pay ve paydayı paya bölmeniz yeterlidir. Örneğin, 18/37 (her iki sayıyı da 18'e bölersiniz) ayarlamadan sonra 1/2,055 olacaktır. Bu da her 2.055 turda bir turun kırmızı ya da siyahla sonuçlanacağı anlamına gelir.
Çoklu dönüşler için olasılık
Tekli dönüşler için hesaplama konusunda uzmanlaştıktan sonra, çoklu dönüşler için olasılığı hesaplamak çok basittir. Tek tek kesirleri birbiriyle çarpmanız yeterlidir.
Örnekler:
- spin - kırmızı üzerine bahis = 18/37
- spin - düzine başına bahis = 12/37
Her iki turu da kazanma olasılığı = (18/37)*(12/37)=1/6,34 veya %15,77 veya 5,34'e 1
- spin - düz bahis - 1/37
- spin - düz bahis - 1/37
Her iki turu da kazanma olasılığı = (1/37)*(1*37)=1/1369 veya %0,073 veya 1368'e 1
- spin - siyah ve tek 9/37 üzerine bahis
- spin - çift 18/37 üzerine bahis
- spin - sütun bahsi 12/37
3 turu da kazanma olasılığı = (9/37)*(18/37)*(12/37)=1/26,06 veya %3,84 veya 1'e 25,06
Girişler arasındaki gerçek dönüşüm yine çok kolaydır. Yüzdeleri, kesri 1/x şeklinde bölerek ve ardından 100 ile çarparak elde edersiniz. Toplamın kazanan turu olan paydadan 1'i çıkararak X'e 1 şeklinde orantılı gösterimi elde edersiniz. Paragrafın üstündeki örneklere bakınız.
Zar olasılığı
Craps, olasılıkları hesaplamanın nispeten kolay olduğu bir başka şans oyunudur. Barbutta kazanma olasılığını hesaplamaya geçmeden önce, zar atma olasılığına bir göz atalım.
Zarın 6 yüzü vardır. Dolayısıyla herhangi bir sayının düşme ihtimali 1/6'dır. Barbut geleneksel olarak iki zarla oynanır. Dolayısıyla herhangi iki sayının bir araya gelme olasılığı 2/36'dır. Ancak, barbutta çok daha önemli olan belirli sayılar kadar bu sayıların toplamıyla da ilgilenmiyoruz. Yine şu formülü kullanacağız: kazanan kombinasyon sayısı/tüm kombinasyonların sayısı.
Diyelim ki 7'nin toplamı için olasılığı bilmek istiyoruz. Kazanan kombinasyonlar: (1-6), (2-4), (3-3), (4-2), (6-1). Gördüğünüz gibi, iki zarda 7 toplamının atılabileceği toplam 6 farklı kombinasyon var. Tüm kombinasyonların sayısı 36 olduğuna göre, 7 olasılığı 6/36=0,1666'dır.
Bu şekilde, diğer tüm olası sonuçlar kolayca hesaplanabilir.
|
Toplam |
Olasılık |
|
2 |
1/36 |
|
3 |
2/36 |
|
4 |
3/36 |
|
5 |
4/36 |
|
6 |
5/36 |
|
7 |
6/36 |
|
8 |
5/36 |
|
9 |
4/36 |
|
10 |
3/36 |
|
11 |
2/36 |
|
12 |
1/36 |
Barbutta kazanma oranları
Kısaca, zar kurallarına bir göz atalım. En yaygın bahis Pass Line'dır.
- Eğer 7 veya 11 atarsanız, kazanırsınız
- Eğer 2, 3 veya 12 atarsanız, kaybedersiniz
- Diğer durumlarda (4, 5, 6, 8, 9 veya 10) bir puan belirlenir ve bu puan tekrar atılana kadar (kazan) veya 7 atılana kadar (kaybet) atılır.
Puanı belirlemeden önce kazanma olasılığını hesaplıyoruz. 7'ye isabet etme şansı 6/36 ve 11'e isabet etme şansı 2/36'dır. Bu iki kesir daha sonra 3/36+2/36 = 2/9 = 0,2222 değerini vermek üzere toplanmalıdır.
Şimdi dikkatimizi bir noktanın belirlendiği duruma çeviriyoruz. Yani, nokta 4, 5, 6, 8, 9 veya 10 olduğunda. Toplam 4 ile başlayalım.
Eğer 4 atılırsa, bir puan belirlenir ve oyuncu 4 veya 7 atana kadar atar. İşte burada koşullu olasılık alanına giriyoruz. Bu bize, B olayının aynı anda gerçekleşmesi durumunda A olayının olasılığının ne olduğunu söyler. Bizim durumumuzda, tur biterse (4 veya 7 atarsa) kazanma olasılığımız (4 atarsa) ne olacaktır. Daha sonra bu değerleri formüle yerleştiririz:
- P(A) = 4'ün düşme toplamı: 3/36
- P(A∩B) = düzeltmelerden sonra A'ya eşit olduğunu buluyoruz
- P(B) = Düşme 4 veya 7: 3/36 + 6/36 = 9/36
Bundan şu sonuç çıkar:
- P(4|4 veya 7) = (3/36)/(9/36) = 1/3
Benzer şekilde 5, 6, 8, 9 ve 10'un toplamlarını da hesaplayabiliriz
- P(5|5 veya 7) = (4/36)/(10/36) = 2/5
- P(6|6 veya 7) = (5/36)/(11/36) = 5/11
- P(8|8 veya 7) = (5/36)/(11/36) = 5/11
- P(9|9 veya 7) = (4/36)/(10/36) = 2/5
- P(10|10 veya 7) = (3/36)/(9/36) = 1/3
Şimdi kazanma şansını, puanın belirlendiği ilk zarın ve oyuncunun kazandığı bir sonraki zarın olasılığı olarak hesaplayabiliriz.
- Orijinal zar 4 x P(4|4 veya 7) = 3/36 x 1/3 = 1/36
- Orijinal zar 5 x P(5|5 veya 7) = 4/36 x 2/5 = 2/45
- Orijinal zar 6 x P(6|6 veya 7) = 5/36 x 5/11 = 25/396
- Orijinal zar 8 x P(8|8 veya 7) = 5/36 x 5/11 = 25/396
- Orijinal zar 9 x P(9|9 veya 7) = 4/36 x 2/5 = 2/45
- Orijinal zar 10 x P(10|10 veya 7) = 3/36 x 1/3 = 1/36
Tüm bu kesirler bize ilk zarın 4, 5, 6, 8, 9 veya 10 olması durumunda kazanma olasılığını verir. Bir Pass hattı bahsinde toplam kazanma olasılığını bilmek istiyorsanız, hepsini toplamanız ve noktadan önce kazanma şansını eklemeniz gerekir (7 veya 11 atar - 2/9).
2/9 + 1/36 + 2/45 + 25/396 + 25/396 + 2/45 + 1/36 = 244/495
Çünkü 244/495 tam olarak %49,3 eder. Bu %50'nin biraz altında. Aslında, muhtemelen 1'de 1 ödeme ile daha iyi bir kazanma şansı bulamazsınız. Belki blackjack hariç, eğer kartları sayabiliyorsanız.
Blackjack Olasılığı
Blackjack, olasılıkların en önemli olduğu şans oyunudur. Blackjack'te, beceriniz ve bilginizle kasa avantajını etkileyebilirsiniz. Bunun için sadece en uygun stratejiyi bilmeniz gerekir ve kartları nasıl sayacağınızı biliyorsanız, oyuncunun avantajıyla bile oynayacaksınız. Aslında tüm özel olasılıkları bilmenize gerek yok, çünkü tüm bu hesaplamalar sizden önce blackjack için tüm taktik ve stratejileri bulan matematikçiler tarafından zaten yapıldı.
Bununla birlikte, ilgi çekmesi açısından, blackjack'teki bazı önemli olgular için olasılığın nasıl hesaplanacağını göstereceğiz.
Olasılık problemine bir iskambil destesi perspektifinden bakarsak, olası sonuçların sayısının hızla arttığı açıktır. Blackjack 52 karttan oluşan bir deste, 4 takım ve 13 değer ile oynanır. Bu da aşağıdaki oranları verir:
- Desteden bir As (veya herhangi bir tek kart) çekerim: 4/52=0,0769 (%7,69)
- Desteden bir maça çekiyorum: 13/52=0,25 (%25)
Ancak, yazı tura, rulet veya slot makinelerinin aksine, bir deste kartın bir tür "hafızası" vardır. Daha doğrusu, önceki sonuçların mevcut ve gelecekteki hamleler üzerinde etkisi olduğu anlamına gelir. Bunun nedeni desteden bir kartın düşmüş olması ve bunun başlangıç durumunu değiştirmesidir. Şimdi 52 kartlık bir desteden ilk kart olarak bir asın çekildiği bir örneğe bakalım (%7,69 şans). Desteden ikinci kart olarak tekrar bir asın çekilme olasılığı şimdi farklı olacaktır. İlk çekilişten sonra as sayısı 3'e ve kart sayısı 51'e düşmüştür.
Blackjack natural için olasılık
Her oyuncunun ilk olarak ilgileneceği şey blackjack olasılığıdır. Yani, bir oyuncunun turun hemen başında bir as ve bir onlu kart alma şansı nedir - başka bir deyişle, bir natürel.
Bu durum iki şekilde ortaya çıkabilir ve iki yolu toplarsak blackjack'teki oranlarımızı elde ederiz:
📌 Not: Tek deste blackjack için sayıyoruz. Yani 52 kart, 4 as ve 16 onlu. Dağıtıcının kartı görünmez, bu nedenle olasılığı etkilemez.
- Oyuncu ilk ası ve bir onlu kartı alır
Oyuncuya 4/52 olasılıkla ilk As kart dağıtılır. Yani oyuncu ikinci kartı onlu almalıdır ve bunun için oranlar 16/51'dir. Bu iki olasılık birbiriyle çarpılarak 16/663 elde edilmelidir.
- Oyuncu ilk onlu kartı ve bir as alır
Bir oyuncunun 10 değerli ilk kartı alma olasılığı 16/52'dir. Bir oyuncunun bundan sonra As alma olasılığı 4/51'dir. Çarpma işleminden sonra 16/663 elde ederiz.
Eğer bir blackjack elde etme olasılığını bilmek istiyorsak, bu iki olguyu toplamamız yeterlidir. Yani 16/663 + 16/663 = 32/663 = %4,827. Başka bir deyişle, bir oyuncu yaklaşık her 20 elde bir blackjack alır. Çok desteli masalar için olasılığı benzer bir şekilde hesaplayabilirsiniz, ki bunu sizin için zaten yaptık.
|
Paket sayısı |
Olasılık |
|
1 |
4,827 % |
|
2 |
4,780 % |
|
3 |
4,764 % |
|
4 |
4,757 % |
|
5 |
4,752 % |
|
6 |
4,749 % |
İflas olasılığı
İflas etme olasılığınızın ne olduğunu bilmek de ilginç olabilir. Yine, tek desteli bir masada sadece krupiye ile oynadığınız örnek bir duruma odaklanacağız. Bir oyuncunun toplam değeri 10 olan 2 karta sahip olduğu ve böylece 20 puana sahip olduğu çok basit bir duruma göz atalım. Oyuncunun üçüncü bir kart aldığı bir durumda, desteden zaten 3 kart oynanmıştır. Bu durumda destede 49 kart kalır. Bu 49 karttan sadece 4 as size yardımcı olacaktır. Bu 49 karttan 45'i istenmeyen kartlardır. Dolayısıyla, baskın olasılığı 45/49=0,9183673'tür.
Diğer olasılıkları da benzer şekilde hesaplayabilirsiniz. Her zaman durumu doğru bir şekilde hayal edebilmeniz gerekir. Hepsi bu kadar.
|
Elin değeri |
İflas olasılığı |
|
21 |
100 % |
|
20 |
92 % |
|
19 |
85 % |
|
18 |
77 % |
|
17 |
69 % |
|
16 |
62 % |
|
15 |
58 % |
|
14 |
56 % |
|
13 |
39 % |
|
12 |
31 % |
|
11 daha az |
0 % |
Şimdi de krupiyenin her kart için iflas etme olasılığına bakalım.
|
Elin değeri |
İflas olasılığı |
|
2 |
35,30 % |
|
3 |
37,56 % |
|
4 |
40,28 % |
|
5 |
42,89 % |
|
6 |
42,08 % |
|
7 |
25,99 % |
|
8 |
23,86 % |
|
9 |
23,34 % |
|
10, J, Q, K |
21,43 % |
|
Ace |
11,65 % |
Poker olasılığı
Poker, olasılığın son derece önemli olduğu bir başka kart oyunudur. Diğer şeylerin yanı sıra. Şimdi pokerde şansınızın ne olduğuna bir göz atalım.
Flop öncesi olasılık
Bir deste kartta olasılığın nasıl işlediğini ana hatlarıyla açıkladığımıza göre, şimdi pratik uygulamalara geçelim. Öncelikle, size bir çiftin (örneğin, çok konuşulan Aslar) tükenme olasılığını nasıl hesaplayacağınızı göstereceğiz. Bu durumda, olasılıkları birbiriyle çarpmamız gerekir.
(4/52) x (3/51) = (12/2652) = (1/221) = 0,004524 (0,45 %)
📌 Not: Saatte yaklaşık 30 el dağıtılan bir kumarhanede poker oynarsanız, yaklaşık her 7 buçuk saatlik oyunda bir çift as elde edersiniz.
Peki, dağıttığınızda 13 olası çiftten herhangi birini elde etme şansınız nedir? Oranların her bir çift için 1/221 olduğunu varsayabiliriz (yukarıdaki formüle bakınız). Bu çiftlerden toplamda 13 tane olabilir, dolayısıyla hesaplama formülü 13/221=0,0588 olacaktır. Yani yaklaşık her 35 maçta bir çift bekleyebilirsiniz.
Pokerde oyuncuya karşı oyuncu olasılığı
Ancak poker, genellikle birbirlerine karşı oynanan çok oyunculu bir oyundur. İşte en yaygın flop öncesi durumlardan bir seçki.
|
Senin elin |
Rakibinizin eli |
Kazanma olasılığı |
|
Yüksek çift |
İki düşük kart |
83 % |
|
Yüksek çift |
Düşük çift |
82 % |
|
Orta çift |
Yüksek, düşük kart |
71 % |
|
İki yüksek kart |
İki düşük kart |
63 % |
|
İki yüksek kart |
Düşük çift |
55 % |
"Outs" ile olasılığın hesaplanması
Flopta kartları görmeyi başarırsanız, elinizi geliştirme şansınızın ne olduğuyla kesinlikle daha fazla ilgileneceksiniz. Bu durumda, sözde "çıkışlar" hakkında konuşacağız. Pokerde bu terim, size yardımcı olabilecek tüm kartları ifade eder. Böyle yaygın bir durum, bir oyuncunun bir renkte iki karta sahip olması ve aynı renkten iki kartın daha flopta görünmesi olabilir. Oyuncunun floş yapmak için 4 kartı vardır ve böylece floş yapmak için 9 kart bırakarak 9 out'a sahip olur.
|
Çıkış sayısı |
Flop - Dönüş |
Dönüş - Nehir |
Bir Nehri Döndür |
|
20 |
42,6 % |
43,5 % |
67,5 % |
|
19 |
40,4 % |
41,3 % |
65,0 % |
|
18 |
38,3 % |
39,1 % |
62,4 % |
|
17 |
36,2 % |
37,0 % |
59,8 % |
|
16 |
34,0 % |
34,8 % |
57,0 % |
|
15 |
31,9 % |
32,6 % |
54,1 % |
|
14 |
29,8 % |
30,4 % |
51,2 % |
|
13 |
27,7 % |
28,3 % |
48,1 % |
|
12 |
25,5 % |
26,1 % |
45,0 % |
|
11 |
23,4 % |
23,9 % |
41,7 % |
|
10 |
21,3 % |
21,7 % |
38,4 % |
|
9 |
19,1 % |
19,6 % |
35,0 % |
|
8 |
17,0 % |
17,4 % |
31,5 % |
|
7 |
14,9 % |
15,2 % |
27,8 % |
|
6 |
12,8 % |
13,0 % |
24,1 % |
|
5 |
10,6 % |
10,9 % |
20,3 % |
|
4 |
8,5 % |
8,7 % |
16,5 % |
|
3 |
6,4 % |
6,5 % |
12,5 % |
|
2 |
4,3 % |
4,3 % |
8,4 % |
|
1 |
2,1 % |
2,2 % |
4,3 % |
📌 Not: Dışarıda kalma olasılığını hesaplamak için hesaplamaları doğrudan masada yapmanıza olanak tanıyan çok kolay bir yöntem vardır. Buna genellikle "dört ve iki" kuralı denir. Floptan sonra, oyuncu dönüş ve nehir olasılığını bulmak için outs sayısını 4 ile çarpar. Eğer dönüşte kartı alamazsa, nehirde kartı alma olasılığını elde etmek için çıkış sayısını iki ile çarpması yeterlidir.
Yine, floptan sonra aynı renkten 4 karta sahip olma örneğini kullanabiliriz. Yani elinizde 9 kart var ve dönüş ve nehirden sonra floş olasılığı %36 (9x4). Diyelim ki turda bir kart almadınız. Bu durumda, çıkışları ikiyle çarparız ve nehirde renkteki kartların tükenme olasılığının %18 (9x2) olduğunu buluruz. Tabloyu karşılaştırarak görebileceğiniz gibi, bu yöntem gerçekten basittir ancak diğer yandan hatalıdır, ancak kullanılabilir.

 TR
TR  English
English  čeština
čeština  Polski
Polski  Slovenčina
Slovenčina  Русский
Русский  Deutsch
Deutsch  Slovenski
Slovenski  Dutch
Dutch  Svenska
Svenska  Português
Português  Italiano
Italiano  Español
Español  Français
Français  Suomalainen
Suomalainen  Български
Български  Românesc
Românesc  Magyar
Magyar  Eesti
Eesti  Ελληνική
Ελληνική  Latviešu
Latviešu  Lietuvių
Lietuvių  やまと
やまと  中国
中国  Dansk
Dansk  ID
ID  Українська
Українська  한국어
한국어  Norsk
Norsk 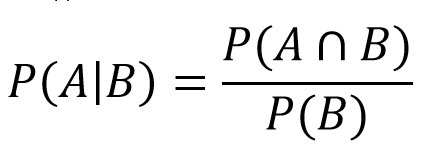


Yorum eklemek için giriş yapmalısınız