Probabilité et jeux de casino
 Peter Sommer
Peter Sommer
Comprenez-vous vos chances ? Si vous allez jouer dans un casino, vous devez vous assurer de connaître vos chances et de les comprendre parfaitement. Pourquoi ? Parce que la probabilité est le moteur qui fait fonctionner les casinos. Sans la probabilité, l'industrie du jeu ne serait pas possible.
Le hasard est simplement la probabilité que quelque chose se produise. Les probabilités font partie de notre vie quotidienne. Lorsque nous décidons de traverser une rue très fréquentée au feu rouge, il y a un certain risque que nous soyons percutés par une voiture, mais en contrepartie, nous avons la possibilité de traverser la rue plus rapidement et de gagner du temps.
Lorsque nous jouons, nous estimons la probabilité qu'un certain événement se produise afin de formuler notre pari. C'est dans ces cas que l'on calcule la probabilité.
💡 Exemple de probabilité
Disons que nous avons un sac contenant quatre balles dont une seule est rouge et les trois autres sont bleues. La probabilité de sortir uniquement la boule rouge sans regarder est de 1 sur 4.
Il existe plusieurs façons d'exprimer la probabilité. On peut aussi dire qu'il y a 3 chances sur 1 contre la rouge, parce qu'en moyenne on tire trois boules bleues pour chaque boule rouge tirée.
Nous pouvons également exprimer nos chances en pourcentage, ainsi notre probabilité de tirer une boule rouge est de 25 % si la probabilité de tirer une boule est de 100 %. Donc 100 divisé par quatre nous donne 25%.
La probabilité de tirer une boule bleue est de 75 % s'il y a trois boules bleues qui ont 25 % de chances d'être tirées.
Probabilité des jeux de casino
Le casino fonctionne sur le principe d'offrir des cotes qui ne sont pas si bonnes que cela compte tenu de notre résultat à long terme.
L'exemple d'un sac de ballons est une façon simple de montrer comment fonctionne un casino. Disons qu'un casino offre une cote de 3 pour tirer une boule rouge. Si vous misez 5 $, alors en moyenne, en quatre tentatives, vous tirerez votre boule bleue 3 fois et perdrez 15 $, et la quatrième fois vous tirerez votre boule rouge et gagnerez 10 $, mais le casino sera toujours dans le noir de 5 $.
Tous les jeux d'argent ne sont qu'une question de probabilité. N'importe quel joueur expérimenté
vous le dira. Il est donc essentiel de connaître ces chiffres et de savoir comment les utiliser. Nous allons donc maintenant vous montrer comment calculer la probabilité dans les jeux d'argent. Si vous comprenez correctement ce principe, vous pouvez l'utiliser pour calculer la probabilité de n'importe quoi d'autre.
Probabilité à la roulette
La roulette est comme la Roue de la Fortune. Et vous savez pourquoi ? Il suffit de trois mots pour l'expliquer : la théorie des grands nombres. Toute personne qui gère un casino ou produit des jeux de casino en ligne connaît très bien cette théorie. Parce qu'elle est directement liée à ses revenus. Et grâce à cela, le casino gagne toujours sur les parieurs à long terme aussi. Tout est lié à la probabilité et à l'avantage de la maison.
📌 Remarque : tous les chiffres de l'article font référence à la roulette européenne - nous comptons donc 37 chiffres.
Comment écrire les probabilités
Il existe plusieurs façons d'écrire les probabilités. Le plus connu est sans doute celui des pourcentages. En plus de celles-ci, des expressions utilisant une fraction ou un rapport sont utilisées.
- Exprimé en pourcentage (%) - il n'y a pas grand-chose à ajouter ici, mais par souci d'exhaustivité, il s'agit du pourcentage pour l'événement sélectionné. Il est calculé comme suit : (Part/Total)*100. Par exemple, la probabilité de tomber sur le numéro sélectionné sur une roulette (Straight) : 1/37*100=2,7%.
- Expression à l'aide de fractions (1/x) - Lorsque l'on exprime une probabilité à l'aide d'une fraction, on dit que le phénomène se produit 1 fois sur X essais. Dans l'expression numérique, nous nous basons sur le calcul de pourcentages. Si nous considérons l'exemple 1/37 ci-dessus, cela signifie qu'un numéro sélectionné statistiquement sur la roulette tombera 1 fois en 37 tours.
- Expression par rapport (x à 1) - Chaque fois que X se produit, le phénomène sélectionné se produit 1 fois. Ici encore, nous nous en tenons à la probabilité du numéro choisi à la roulette. Dans ce cas, le rapport sera écrit comme suit : 36 pour 1. Cela signifie qu'après chaque 36 tours où le numéro ne tombe pas, il y aura un cas où le numéro sélectionné tombe.
📌 Note : Comme le dit la théorie des grands nombres, la probabilité est essentiellement une limite mathématique. Avec de plus en plus d'essais, vous vous rapprochez de manière réaliste du résultat calculé.
Comme vous pouvez le constater, les expressions utilisant des fractions et celles utilisant des ratios sont très similaires. La seule différence est qu'une fraction compte tous les tours, tandis qu'un ratio divise le total des tours en deux catégories.
Tableau des probabilités pour les mises individuelles à la roulette
|
Mise |
Extrait de |
Ratio |
Pourcentages |
|
Une mise directe |
1/2,055 |
1,055 à 1 |
48,6 % |
|
Colonne |
1/3,08 |
2,08 contre 1 |
32,4 % |
|
La douzaine |
1/3,08 |
2,08 contre 1 |
32,4 % |
|
Six Line |
1/6,17 |
5,17 contre 1 |
16,2 % |
|
Corner |
1/9,25 |
8,25 contre 1 |
10,8 % |
|
Rue |
1/12,33 |
11,33 contre 1 |
8,1 % |
|
Split |
1/19,5 |
18,5 contre 1 |
5,4 % |
|
Droit |
1/37 |
36 à 1 |
2,7 % |
Probabilité d'une mise directe
Une comparaison mathématique pour la répétition du phénomène sélectionné pourrait également être intéressante. Dans ce cas, nous avons choisi une mise directe, c'est-à-dire par exemple une mise sur le rouge. Ainsi, quelle sera la probabilité de changement de rouge 5 fois de suite, par exemple ?
|
Nombre de tours |
Ratio |
Pourcentages |
|
1 |
1,06 à 1 |
48,6 % |
|
2 |
3,23 contre 1 |
23,7 % |
|
3 |
7,69 contre 1 |
11,5 % |
|
4 |
16,9 contre 1 |
5,6 % |
|
5 |
35,7 contre 1 |
2,73 % |
|
6 |
74,4 contre 1 |
1,33 % |
|
7 |
154 à 1 |
0,65 % |
|
8 |
318 à 1 |
0,31 % |
|
9 |
654 à 1 |
0,15 % |
|
10 |
1 346 à 1 |
0,074 % |
|
15 |
49 423 à 1 |
0,002 % |
|
20 |
1 813 778 à 1 |
0,000055 % |
Comme on peut le constater, plus le nombre de spins augmente, plus la probabilité de ce phénomène diminue rapidement. Toutefois, il faut garder à l'esprit que ces probabilités décrivent le phénomène dans son ensemble. Le générateur de nombres aléatoires ne tient pas compte des résultats précédents. Ainsi, même si une série de jeux où le rouge frappe 20 fois de suite se produit une fois tous les 1,813 million de jeux, une série de 21 jeux aura le même avantage de la maison et la même probabilité (c'est-à-dire 48,6 %) que toutes les autres séries de jeux.
Souvent, dans ce cas, on peut rencontrer le terme Player's Fallacy, où le parieur croit que si une couleur est touchée plusieurs fois de suite, il y a une plus grande probabilité que l'autre couleur soit touchée au prochain tour. En réalité, ce n'est pas le cas. Le cas le plus célèbre de cette erreur a été observé en 1913 au casino de Monte-Carlo, lorsque le noir est tombé 26 fois de suite sur la roulette. Pendant presque toute la durée de cette incroyable série, et même après sa fin, les gens ont parié frénétiquement sur le rouge. C'est à ce moment-là que le casino a gagné beaucoup d'argent.
📌 Remarque : la probabilité qu'une couleur soit touchée 26 fois de suite est de 0,000000730870% et se produit une fois sur 67 millions de parties.
Comment calculer la probabilité de la roulette
Vous voulez connaître d'autres cotes pour les paris individuels ? Essayez de les calculer vous-même. Travailler avec des pourcentages et des probabilités n'est pas très compliqué. En général, le plus simple est de commencer par les fractions et de les utiliser pour calculer d'autres pourcentages et ratios. Par exemple, si vous voulez calculer la probabilité dans une fraction pour une situation où le rouge est rouge, vous faites ce qui suit :
Nombre total de rouges sur le terrain de jeu/Nombre total de terrains de jeu = 18/37
Probabilité pour un tour
Là encore, une règle simple s'applique. Il suffit de calculer le nombre de champs qui vous permettront de gagner et de le diviser par le nombre total de champs.
Par exemple :
- Couleur - 18/37
- Sudá/Lichá - 18/37
- Douzaine - 12/37
- Numéro 0 - 1/37
- Noir et pair - 9/37 (il n'y a que 9 numéros dans le champ de jeu qui sont à la fois noirs et pairs).
- Douzaine et colonne - 4/37 (il n'y a que 4 numéros dans une douzaine et dans une colonne)
Tout comme la probabilité de gagner, vous pouvez calculer la probabilité de perdre. Il suffit de compter le nombre de champs non gagnants et de le diviser à nouveau par le nombre total de champs. Par exemple, la probabilité de perdre si vous misez sur le rouge est de 19/37 (18 champs noirs + zéro vert).
📌 Remarque : Pour réduire une fraction à 1/x, il suffit de diviser le numérateur et le dénominateur par le numérateur. Par exemple, 18/37 (vous divisez les deux nombres par 18) sera 1/2,055 après l'ajustement. Cela signifie donc que pour 2,055 tours, un tour donnera lieu à un rouge ou à un noir.
Probabilité de spins multiples
Une fois que vous avez maîtrisé le calcul pour les tours simples, le calcul de la probabilité pour les tours multiples est très simple. Il suffit de multiplier les fractions individuelles les unes par les autres.
Exemples :
- spin - pari sur le rouge = 18/37
- spin - pari par douzaine = 12/37
Probabilité de gagner les deux tours = (18/37)*(12/37)=1/6,34 ou 15,77% ou 5,34 contre 1
- spin - pari direct - 1/37
- spin - pari direct - 1/37
Probabilité de gagner les deux tours = (1/37)*(1*37)=1/1369 ou 0,073% ou 1368 à 1
- spin - parier sur le noir et l'impair 9/37
- spin - pari sur pair 18/37
- spin - colonne pari 12/37
Probabilité de gagner les 3 tours = (9/37)*(18/37)*(12/37)=1/26,06 ou 3,84% ou 25,06 à 1
La conversion réelle entre les entrées est à nouveau très facile. Vous obtenez les pourcentages en divisant la fraction sous la forme 1/x puis en la multipliant par 100. Vous obtenez la notation proportionnelle sous la forme de X à 1 en soustrayant 1 du dénominateur, qui est le tour gagnant du total. Voir les exemples au-dessus du paragraphe.
Probabilité des dés
Le craps est un autre jeu de hasard dans lequel il est relativement facile de calculer les probabilités. Avant de calculer les chances de gagner au craps, examinons la probabilité des lancers de dés eux-mêmes.
Les dés ont 6 faces. La probabilité qu'un nombre quelconque tombe est donc de 1/6. Le craps se joue traditionnellement avec deux dés. Les chances de combiner deux numéros sont donc de 2/36. Cependant, nous ne sommes pas tant intéressés par les chiffres spécifiques que par la somme de ces chiffres, ce qui est beaucoup plus important au craps. Là encore, nous utiliserons la formule suivante : nombre de combinaisons gagnantes/nombre de toutes les combinaisons.
Disons que nous voulons connaître la probabilité de la somme de 7. Combinaisons gagnantes : (1-6), (2-4), (3-3), (4-2), (6-1). Comme vous pouvez le constater, il existe un total de 6 combinaisons différentes où la somme de 7 peut être obtenue sur deux dés. Et comme le nombre de toutes les combinaisons est de 36, la probabilité de 7 est de 6/36=0,1666.
De cette façon, tous les autres résultats possibles peuvent être facilement calculés.
|
Total |
Probabilité |
|
2 |
1/36 |
|
3 |
2/36 |
|
4 |
3/36 |
|
5 |
4/36 |
|
6 |
5/36 |
|
7 |
6/36 |
|
8 |
5/36 |
|
9 |
4/36 |
|
10 |
3/36 |
|
11 |
2/36 |
|
12 |
1/36 |
Les chances de gagner au craps
Brièvement, jetons un coup d'œil aux règles des dés. Le pari le plus courant est la ligne de passe.
- Si vous obtenez un 7 ou un 11, vous gagnez.
- Si vous obtenez un 2, 3 ou 12, vous perdez.
- Dans les autres cas (4, 5, 6, 8, 9 ou 10), un point est déterminé et lancé jusqu'à ce que ce point soit relancé (victoire) ou qu'un 7 soit lancé (défaite).
Nous calculons d'abord la probabilité de gagner avant de déterminer le point. La chance de toucher 7 est de 6/36 et la chance de toucher 11 est de 2/36. Il faut alors additionner ces deux fractions pour obtenir 3/36+2/36 = 2/9 = 0,2222.
Nous nous intéressons maintenant à la situation où un point est déterminé. C'est-à-dire lorsque le point est 4, 5, 6, 8, 9 ou 10. Commençons par un total de 4.
Si un 4 est obtenu, un point est déterminé et le joueur lance le dé jusqu'à ce qu'il obtienne un 4 ou un 7. C'est là que nous entrons dans le domaine de la probabilité conditionnelle. Cela nous indique quelle est la probabilité de l'événement A si l'événement B se produit au même moment. Dans notre cas, ce sera la probabilité que nous gagnions (obtient un 4) si le tour se termine (obtient un 4 ou un 7). Nous introduisons ensuite ces valeurs dans la formule :
- P(A) = Somme de chutes de 4 : 3/36
- P(A∩B) = après ajustements, nous trouvons qu'il est égal à A.
- P(B) = Chutes 4 ou 7 : 3/36 + 6/36 = 9/36
Il s'ensuit que :
- P(4|4 ou 7) = (3/36)/(9/36) = 1/3
De la même manière, nous pouvons calculer les sommes de 5, 6, 8, 9 et 10
- P(5|5 ou 7) = (4/36)/(10/36) = 2/5
- P(6|6 ou 7) = (5/36)/(11/36) = 5/11
- P(8|8 ou 7) = (5/36)/(11/36) = 5/11
- P(9|9 ou 7) = (4/36)/(10/36) = 2/5
- P(10|10 ou 7) = (3/36)/(9/36) = 1/3
Maintenant, nous pouvons calculer la chance de gagner comme la probabilité du lancer initial lorsque le point a été déterminé et du lancer suivant lorsque le joueur a gagné.
- Jet initial 4 x P(4|4 ou 7) = 3/36 x 1/3 = 1/36
- Jet initial 5 x P(5|5 ou 7) = 4/36 x 2/5 = 2/45
- Jet initial 6 x P(6|6 ou 7) = 5/36 x 5/11 = 25/396
- Jet initial 8 x P(8|8 ou 7) = 5/36 x 5/11 = 25/396
- Jet initial 9 x P(9|9 ou 7) = 4/36 x 2/5 = 2/45
- Jet initial 10 x P(10|10 ou 7) = 3/36 x 1/3 = 1/36
Toutes ces fractions nous donnent la probabilité de gagner si le premier jet est 4, 5, 6, 8, 9 ou 10. Si vous voulez connaître la probabilité totale de gagner sur un pari Pass line, vous devez les additionner et ajouter la chance de gagner avant le point (lancer un 7 ou un 11 - 2/9).
2/9 + 1/36 + 2/45 + 25/396 + 25/396 + 2/45 + 1/36 = 244/495
Parce que 244/495 fait exactement 49,3%. C'est un peu moins de 50 %. En fait, vous ne trouverez probablement pas de meilleure chance de gagner avec un gain de 1 sur 1. Sauf peut-être le blackjack, si vous savez compter les cartes.
Probabilité de Blackjack
Le blackjack est le jeu de hasard dans lequel les chances sont les plus importantes. Au blackjack, vous pouvez influencer l'avantage de la maison grâce à vos compétences et à vos connaissances. Il vous suffit de connaître la stratégie optimale pour cela, et si vous savez compter les cartes, vous jouerez même avec l'avantage du joueur. En fait, vous n'avez pas besoin de connaître toutes les probabilités spécifiques, car tous ces calculs ont déjà été effectués par des mathématiciens avant vous qui ont imaginé toutes les tactiques et stratégies pour le blackjack.
Cependant, par souci d'intérêt, nous allons montrer comment calculer la probabilité de certains phénomènes importants au blackjack.
Si l'on considère le problème des probabilités du point de vue d'un jeu de cartes, il est clair que le nombre de résultats possibles augmente rapidement. Le blackjack se joue avec un jeu de 52 cartes, 4 couleurs et 13 valeurs. Cela donne les cotes suivantes :
- Je tire un As du jeu (ou une carte individuelle) : 4/52=0.0769 (7.69%)
- Je tire un pique du jeu : 13/52=0.25 (25%)
Cependant, contrairement au tirage au sort, à la roulette ou aux machines à sous par exemple, un jeu de cartes a une sorte de "mémoire". Ou plutôt, cela signifie que les résultats précédents ont un effet sur les mouvements actuels et futurs. Cela est dû au fait qu'une carte a été retirée du jeu et que cela change la situation de départ. Prenons un exemple où la première carte tirée d'un jeu de 52 cartes est un As (7,69 % de chances). La probabilité qu'un As soit à nouveau tiré comme deuxième carte du jeu sera maintenant différente. Après le premier tirage, le nombre d'as est tombé à 3 et le nombre de cartes à 51.
Probabilité pour le blackjack naturel
Ce qui intéresse d'abord tout joueur, c'est la probabilité du blackjack. C'est-à-dire quelles sont les chances qu'un joueur obtienne un as et un dix dès le début du tour - en d'autres termes, un naturel.
Cette situation peut se produire de deux façons, et si nous additionnons les deux façons, nous obtenons nos chances au blackjack :
📌 Note : Nous comptons pour un blackjack à un seul jeu de cartes. Donc 52 cartes, 4 as et 16 10. La carte du croupier n'est pas visible, elle n'affecte donc pas la probabilité.
- Le joueur obtient le premier as et une carte de dix.
Le joueur reçoit la première carte As avec une probabilité de 4/52. Le joueur doit donc obtenir la deuxième carte avec un dix, et pour cela la cote est de 16/51. Ces deux probabilités doivent être multipliées ensemble pour obtenir 16/663.
- Le joueur reçoit la première carte dix et un as.
La probabilité qu'un joueur reçoive la première carte avec une valeur de 10 est de 16/52. Les chances qu'un joueur obtienne un As après cela sont de 4/51. Après avoir multiplié, on obtient 16/663.
Si l'on veut connaître la probabilité d'obtenir un blackjack, il suffit d'additionner ces deux phénomènes. Donc 16/663 + 16/663 = 32/663 = 4,827%. En d'autres termes, un joueur obtient un blackjack environ une fois toutes les 20 mains. Vous pouvez calculer la probabilité pour les tables à plusieurs jeux de cartes de la même manière, ce que nous avons déjà fait pour vous.
|
Nombre de paquets |
Probabilité |
|
1 |
4,827 % |
|
2 |
4,780 % |
|
3 |
4,764 % |
|
4 |
4,757 % |
|
5 |
4,752 % |
|
6 |
4,749 % |
Probabilité d'une rupture
Il pourrait également être intéressant de savoir quelles sont vos chances de faire un échec. Encore une fois, nous nous concentrerons sur un exemple de situation où vous jouez uniquement avec le croupier à une table à un seul jeu de cartes. Prenons une situation très simple : un joueur possède 2 cartes d'une valeur de 10 au total, ce qui lui donne 20 points. Dans une situation où le joueur obtient une troisième carte, 3 cartes ont déjà été jouées de la pioche. Il reste donc 49 cartes dans le jeu. Sur ces 49 cartes, seuls 4 as vous seront utiles. Sur ces 49 cartes, 45 sont indésirables. Par conséquent, les chances d'un buste sont de 45/49=0.9183673.
Vous pouvez calculer d'autres probabilités de la même manière. Il faut toujours être capable d'imaginer la situation correctement. C'est tout.
|
Valeur de la main |
Probabilité de busts |
|
21 |
100 % |
|
20 |
92 % |
|
19 |
85 % |
|
18 |
77 % |
|
17 |
69 % |
|
16 |
62 % |
|
15 |
58 % |
|
14 |
56 % |
|
13 |
39 % |
|
12 |
31 % |
|
11 moins |
0 % |
Voyons maintenant quelle est la probabilité que le croupier fasse un bust pour chaque carte.
|
Valeur de la main |
Probabilité de busts |
|
2 |
35,30 % |
|
3 |
37,56 % |
|
4 |
40,28 % |
|
5 |
42,89 % |
|
6 |
42,08 % |
|
7 |
25,99 % |
|
8 |
23,86 % |
|
9 |
23,34 % |
|
10, J, Q, K |
21,43 % |
|
Ace |
11,65 % |
Probabilité de poker
Le poker est un autre jeu de cartes où la probabilité est extrêmement importante. Entre autres choses. Voyons donc quelles sont vos chances au poker.
Probabilité de pré-flop
Maintenant que nous avons décrit comment la probabilité fonctionne dans un jeu de cartes, passons aux applications pratiques. Tout d'abord, nous allons montrer comment calculer la probabilité de ne pas avoir de paires dans une main. (par exemple, les As, dont on parle beaucoup). Dans ce cas, nous devons multiplier les probabilités les unes par les autres.
(4/52) x (3/51) = (12/2652) = (1/221) = 0,004524 (0,45 %)
📌 Remarque : si vous jouez au poker dans un casino qui distribue environ 30 mains par heure, vous obtiendrez une paire d'as environ une fois toutes les 7 heures et demie de jeu.
Quelles sont donc les chances d'obtenir l'une des 13 paires possibles lorsque vous distribuez ? Nous pouvons supposer que les chances sont de 1/221 par paire individuelle (voir la formule ci-dessus). Il peut y avoir 13 de ces paires au total, la formule de calcul sera donc 13/221=0,0588. Vous pouvez donc vous attendre à une paire tous les 35 jeux environ.
Probabilité au poker joueur contre joueur
Cependant, le poker est un jeu multijoueurs, qui se joue généralement les uns contre les autres. Voici donc une sélection des situations pré-flop les plus courantes.
|
Votre main |
Main de votre adversaire |
Probabilité de gagner |
|
Haute paire |
Deux cartes basses |
83 % |
|
Haute paire |
Paire basse |
82 % |
|
Paire du milieu |
Carte haute, carte basse |
71 % |
|
Deux cartes hautes |
Deux cartes basses |
63 % |
|
Deux cartes hautes |
Paire basse |
55 % |
Calcul de la probabilité par les " outs ".
Si vous parvenez à voir les cartes du flop, vous serez certainement plus intéressé par vos chances d'améliorer votre main. Dans ce cas, nous parlerons de ce que l'on appelle les "outs". Au poker, ce terme désigne toutes les cartes qui peuvent vous aider. Un tel cas de figure peut se produire lorsqu'un joueur détient deux cartes dans une couleur et que deux autres cartes de la même couleur apparaissent sur le flop. Le joueur dispose alors de 4 cartes pour la couleur et a donc 9 outs, ce qui lui laisse 9 cartes avec lesquelles il peut former une couleur.
|
Nombre de sorties |
Flop - Turn |
Turn - River |
Tourner une rivière |
|
20 |
42,6 % |
43,5 % |
67,5 % |
|
19 |
40,4 % |
41,3 % |
65,0 % |
|
18 |
38,3 % |
39,1 % |
62,4 % |
|
17 |
36,2 % |
37,0 % |
59,8 % |
|
16 |
34,0 % |
34,8 % |
57,0 % |
|
15 |
31,9 % |
32,6 % |
54,1 % |
|
14 |
29,8 % |
30,4 % |
51,2 % |
|
13 |
27,7 % |
28,3 % |
48,1 % |
|
12 |
25,5 % |
26,1 % |
45,0 % |
|
11 |
23,4 % |
23,9 % |
41,7 % |
|
10 |
21,3 % |
21,7 % |
38,4 % |
|
9 |
19,1 % |
19,6 % |
35,0 % |
|
8 |
17,0 % |
17,4 % |
31,5 % |
|
7 |
14,9 % |
15,2 % |
27,8 % |
|
6 |
12,8 % |
13,0 % |
24,1 % |
|
5 |
10,6 % |
10,9 % |
20,3 % |
|
4 |
8,5 % |
8,7 % |
16,5 % |
|
3 |
6,4 % |
6,5 % |
12,5 % |
|
2 |
4,3 % |
4,3 % |
8,4 % |
|
1 |
2,1 % |
2,2 % |
4,3 % |
📌 Remarque : Il existe une méthode très simple pour calculer la probabilité des outs, vous pouvez donc le faire directement à la table. On l'appelle généralement la règle du "quatre et deux". Après le flop, le joueur multiplie simplement le nombre d'outs par 4 pour trouver la probabilité pour la turn et la river. S'il n'obtient pas la carte au tournant, il multiplie simplement le nombre de sorties par deux pour obtenir la probabilité approximative d'obtenir la carte à la rivière.
Encore une fois, nous pouvons utiliser l'exemple d'avoir 4 cartes de la même couleur après le flop. Donc vos outs sont de 9 cartes et la probabilité d'une couleur après le turn et la river est de 36% (9x4). Disons que vous ne recevez pas de carte au tour. Dans ce cas, nous multiplions les outs par deux et nous trouvons que nous avons 18% (9x2) de chances d'être à court de cartes dans la couleur sur la rivière. Comme vous pouvez le voir en comparant le tableau, cette méthode est vraiment simple mais d'un autre côté inexacte, mais elle peut être utilisée.

 FR
FR  English
English  čeština
čeština  Polski
Polski  Slovenčina
Slovenčina  Русский
Русский  Deutsch
Deutsch  Slovenski
Slovenski  Dutch
Dutch  Svenska
Svenska  Português
Português  Italiano
Italiano  Español
Español  Suomalainen
Suomalainen  Български
Български  Românesc
Românesc  Magyar
Magyar  Eesti
Eesti  Ελληνική
Ελληνική  Latviešu
Latviešu  Lietuvių
Lietuvių  やまと
やまと  中国
中国  Dansk
Dansk  Türkçe
Türkçe  ID
ID  Українська
Українська  한국어
한국어  Norsk
Norsk 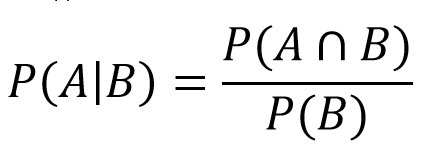


Vous devez être connecté pour ajouter un commentaire