Waarschijnlijkheid en casinospelen
 Peter Sommer
Peter Sommer
Begrijp je je kansen? Als u in een casino gaat spelen, moet u ervoor zorgen dat u uw kansen kent en ze perfect begrijpt. Waarom? Omdat waarschijnlijkheid de motor is die casino's laat werken. Zonder waarschijnlijkheid zou de gokindustrie niet mogelijk zijn.
Kans is gewoon de waarschijnlijkheid dat iets zal gebeuren. Waarschijnlijkheid maakt deel uit van ons dagelijks leven. Wanneer wij besluiten een drukke straat voor een rood licht over te steken, bestaat er een zekere kans dat wij door een auto worden aangereden, maar in ruil daarvoor hebben wij de kans om sneller over te steken en wat tijd over te houden.
Als we gokken, schatten we de kans dat een bepaalde gebeurtenis zich voordoet, om onze weddenschap te formuleren. Het is in deze gevallen dat wij de waarschijnlijkheid berekenen.
💡 Voorbeeld van waarschijnlijkheid
Laten we zeggen dat we een zak hebben met vier ballen waarvan er maar één rood is en de andere drie blauw. De kans dat je alleen de rode bal eruit trekt zonder te kijken is 1 op 4.
Er zijn verschillende manieren om waarschijnlijkheid uit te drukken. We kunnen ook zeggen dat er een kans van 3 op 1 is tegen rood, omdat we gemiddeld drie blauwe ballen trekken voor elke getrokken rode bal.
We kunnen onze kansen ook uitdrukken als percentage, dus onze kans om een rode bal te trekken is 25% als er 100% kans is om een bal te trekken. Dus 100 gedeeld door vier geeft ons 25%.
De kans om een blauwe bal te trekken is 75% als er drie blauwe ballen zijn met 25% kans om te trekken.
Waarschijnlijkheid van casinospelen
Het casino werkt volgens het principe van het aanbieden van kansen die niet zo goed zijn gezien ons resultaat op lange termijn.
Het voorbeeld van een zak ballonnen is een eenvoudige manier om te laten zien hoe een casino werkt. Laten we zeggen dat een casino een winkans van 3 biedt om een rode bal te trekken. Als u $5 inzet, dan zult u gemiddeld, in vier pogingen, uw blauwe bal 3 keer trekken en $15 verliezen, en bij de vierde keer trekt u uw rode bal en wint $10, maar het casino zal nog steeds $5 in het zwart staan.
Alle gokken gaat gewoon over waarschijnlijkheid. Elke ervaren gokker
zal je dat vertellen. Het is dus van essentieel belang met deze getallen vertrouwd te zijn en te weten hoe ermee te werken. Dus hier zullen we u nu laten zien hoe u de kansberekening bij gokken maakt. Als je het principe goed begrijpt, kun je het gebruiken om de waarschijnlijkheid van iets anders te berekenen.
Waarschijnlijkheid bij roulette
Roulette is als het Rad van Fortuin. En weet je waarom? Er zijn maar 3 woorden nodig om het uit te leggen - Big Number Theory. Iedereen die een casino runt of online casinospelen produceert, kent deze theorie zeer goed. Omdat het direct gekoppeld is aan zijn verdiensten. En dankzij dat wint het casino op de lange termijn ook altijd van de gokkers. Alles heeft te maken met waarschijnlijkheid en het huisvoordeel.
Opmerking: Alle getallen in het artikel verwijzen naar Europees Roulette - dus tellen we 37 getallen.
Hoe schrijf je waarschijnlijkheid
Er zijn verschillende manieren om waarschijnlijkheid te schrijven. De bekendste zijn waarschijnlijk de percentages. Daarnaast worden uitdrukkingen met een breuk of een verhouding gebruikt.
- Uitgedrukt als percentage (%) - hier valt niet veel aan toe te voegen, maar voor de volledigheid, dit is het percentage voor de geselecteerde gebeurtenis. Het wordt berekend als (Deel/Totaal)*100. Bijvoorbeeld, de kans om het gekozen nummer te raken op een roulette wiel (Straight): 1/37*100=2.7%
- Uitdrukking met breuken (1/x) - Bij het uitdrukken van de waarschijnlijkheid met behulp van een breuk, zeggen we dat het verschijnsel zich 1 keer voordoet op X proeven. In een numerieke uitdrukking vertrouwen we op het berekenen van percentages. Als we het bovenstaande voorbeeld van 1/37 nemen, betekent dit dat een statistisch gekozen getal op het roulettewiel 1 keer in 37 spins zal vallen.
- Uitdrukking door verhouding (x tot 1) - Telkens wanneer X optreedt, gebeurt het gekozen verschijnsel 1 keer. Ook hier houden we ons aan de waarschijnlijkheid voor het gekozen nummer bij roulette. In dit geval wordt de verhouding geschreven als 36 tot 1. Dit betekent dat na elke 36 spins waar het nummer niet valt, er één keer zal zijn waar het geselecteerde nummer valt.
Opmerking: Zoals de grote getallenleer zegt, is waarschijnlijkheid in wezen een wiskundige limiet. Met meer en meer proeven komt u realistisch gezien steeds dichter bij het berekende resultaat.
Zoals je ziet, lijken de uitdrukkingen met breuken en met verhoudingen erg op elkaar. Het enige verschil is dat een breuk alle spins telt, terwijl een ratio het totaal aantal spins in twee categorieën opsplitst.
Tabel van kansen voor individuele inzetten bij roulette
|
Weddenschap |
Uittreksel uit |
Verhouding |
Percentages |
|
Een straight bet |
1/2,055 |
1,055 tot 1 |
48,6 % |
|
Kolom |
1/3,08 |
2,08 tegen 1 |
32,4 % |
|
De Dozijn |
1/3,08 |
2,08 tegen 1 |
32,4 % |
|
Six Line |
1/6,17 |
5,17 tegen 1 |
16,2 % |
|
Hoek |
1/9,25 |
8,25 tegen 1 |
10,8 % |
|
Straat |
1/12,33 |
11,33 tegen 1 |
8,1 % |
|
Split |
1/19,5 |
18,5 tegen 1 |
5,4 % |
|
Recht |
1/37 |
36 tegen 1 |
2,7 % |
Waarschijnlijkheid voor een straight bet
Een mathematische vergelijking voor de herhaling van het gekozen verschijnsel zou ook interessant kunnen zijn. In dit geval hebben wij gekozen voor een straight bet, bijvoorbeeld een inzet op rood. Dus, wat is de veranderende kans op bijvoorbeeld 5 keer rood op een rij?
|
Aantal spins |
Verhouding |
Percentages |
|
1 |
1,06 tegen 1 |
48,6 % |
|
2 |
3,23 tegen 1 |
23,7 % |
|
3 |
7,69 tegen 1 |
11,5 % |
|
4 |
16,9 tegen 1 |
5,6 % |
|
5 |
35,7 tegen 1 |
2,73 % |
|
6 |
74,4 tegen 1 |
1,33 % |
|
7 |
154 tegen 1 |
0,65 % |
|
8 |
318 tegen 1 |
0,31 % |
|
9 |
654 tegen 1 |
0,15 % |
|
10 |
1 346 tegen 1 |
0,074 % |
|
15 |
49 423 tegen 1 |
0,002 % |
|
20 |
1 813 778 aan 1 |
0,000055 % |
Zoals men kan zien, neemt de waarschijnlijkheid van dit verschijnsel snel af naarmate het aantal spins toeneemt. Bedenk echter dat deze waarschijnlijkheden het verschijnsel in zijn geheel beschrijven. De willekeurige getallengenerator houdt geen rekening met eerdere uitkomsten, dus ook al komt een spelreeks waarbij rood 20 keer achter elkaar slaat eens in de 1,813 miljoen spellen voor, toch zal een 21-spelronde hetzelfde huisvoordeel en dezelfde waarschijnlijkheid (d.w.z. 48,6%) hebben als elke andere spelronde.
Vaak kan men in dit geval de term Player's Fallacy tegenkomen, waarbij de gokker gelooft dat als een kleur meerdere keren achter elkaar wordt geraakt, er een grotere kans is dat de andere kleur bij de volgende draai zal worden geraakt. In werkelijkheid is dit niet het geval. Het beroemdste geval van deze misvatting werd waargenomen in 1913 in het Casino van Monte Carlo, toen zwart 26 keer na elkaar viel op het roulettewiel, en gedurende bijna de gehele periode van deze ongelooflijke reeks, en zelfs nadat deze was afgelopen, wedden de mensen koortsachtig op rood. Toen verdiende het casino heel veel geld.
Opmerking: De kans dat een kleur 26 keer na elkaar wordt geraakt is 0,000000730870% en komt één keer voor in 67 miljoen spellen.
Hoe bereken je de waarschijnlijkheid van roulette
Wil je meer kansen weten voor individuele weddenschappen? Probeer ze zelf uit te rekenen. Werken met percentages en waarschijnlijkheden is niet erg ingewikkeld. Over het algemeen is het het gemakkelijkst om met breuken te beginnen en die te gebruiken om verdere percentages en verhoudingen te berekenen. Als je bijvoorbeeld de kans in een breuk wilt berekenen voor een situatie waarin het rood is, doe je het volgende:
Totaal aantal roden op het speelveld/Totaal aantal speelvelden = 18/37
Waarschijnlijkheid voor één draai
Ook hier geldt een eenvoudige regel. Bereken gewoon het aantal velden dat u een winst oplevert en deel dat door het totale aantal velden.
Bijvoorbeeld:
- Kleur - 18/37
- Sudá/Lichá - 18/37
- Dozijn - 12/37
- Nummer 0 - 1/37
- Zwart en even - 9/37 (er zijn slechts 9 nummers in het speelveld die zowel zwart als even zijn)
- Dozijn en kolom - 4/37 (er zijn slechts 4 getallen in een dozijn en in een kolom)
Net als de kans om te winnen, kun je ook de kans om te verliezen berekenen. Tel gewoon het aantal niet-winnende velden en deel ze opnieuw door het totale aantal velden. Bijvoorbeeld, de kans dat u verliest als u op rood wedt is 19/37 (18 zwarte velden + groene nul).
Opmerking: Om een breuk te herleiden tot 1/x, deel je gewoon de teller en de noemer door de teller. Bijvoorbeeld, 18/37 (u deelt beide getallen door 18) zal 1/2.055 zijn na de aanpassing. Dit betekent dus dat voor elke 2,055 beurten, één beurt zal resulteren in een rode of een zwarte.
Waarschijnlijkheid van meerdere spins
Als je eenmaal de berekening voor single spins onder de knie hebt, is het berekenen van de kans voor multiple spins heel eenvoudig. Vermenigvuldig gewoon de afzonderlijke breuken met elkaar.
Voorbeelden:
- draai - inzet op rood = 18/37
- draai - inzet per dozijn = 12/37
Kans om beide rondes te winnen = (18/37)*(12/37)=1/6,34 of 15,77% of 5,34 tegen 1
- draai - straight bet - 1/37
- draai - straight bet - 1/37
Kans om beide rondes te winnen = (1/37)*(1*37)=1/1369 of 0.073% of 1368 tegen 1
- draai - inzet op zwart en oneven 9/37
- draai - weddenschap op even 18/37
- draai - kolom inzet 12/37
Kans om alle 3 de rondes te winnen = (9/37)*(18/37)*(12/37)=1/26.06 of 3.84% of 25.06 tot 1
De eigenlijke omzetting tussen de ingangen is opnieuw zeer eenvoudig. Je krijgt de percentages door de breuk te delen in de vorm 1/x en dan te vermenigvuldigen met 100. Je krijgt de proportionele notatie in de vorm van X tot 1 door 1 af te trekken van de noemer, die de winnende ronde is van het totaal. Zie de voorbeelden boven de alinea.
Waarschijnlijkheid van dobbelen
Craps is een ander kansspel waarbij het relatief eenvoudig is om de kansen te berekenen. Voordat we beginnen met het berekenen van de winkansen bij craps, kijken we eerst naar de waarschijnlijkheid van de dobbelstenen zelf.
De dobbelstenen hebben 6 zijden. De kans dat een getal valt is dus 1/6. Craps wordt traditioneel gespeeld met twee dobbelstenen. De kans dat twee getallen samenkomen is dus 2/36. We zijn echter niet zozeer geïnteresseerd in de specifieke getallen als wel in de som van die getallen, wat veel belangrijker is bij craps. Ook hier gebruiken we de formule: aantal winnende combinaties/aantal van alle combinaties.
Laten we zeggen dat we de kans willen weten voor de som van 7. Winnende combinaties: (1-6), (2-4), (3-3), (4-2), (6-1). Zoals u kunt zien, zijn er in totaal 6 verschillende combinaties waarbij de som van 7 op twee dobbelstenen kan worden gegooid. En aangezien het aantal van alle combinaties 36 is, is de kans op 7 6/36=0.1666
Op deze manier kunnen alle andere mogelijke resultaten gemakkelijk worden berekend.
|
Totaal |
Waarschijnlijkheid |
|
2 |
1/36 |
|
3 |
2/36 |
|
4 |
3/36 |
|
5 |
4/36 |
|
6 |
5/36 |
|
7 |
6/36 |
|
8 |
5/36 |
|
9 |
4/36 |
|
10 |
3/36 |
|
11 |
2/36 |
|
12 |
1/36 |
Kansen om te winnen bij craps
Laten we eens kort kijken naar de dobbelsteenregels. De meest voorkomende weddenschap is de Pass Line.
- Als je een 7 of 11 gooit, win je.
- Als je een 2, 3 of 12 gooit, verlies je
- In andere gevallen (4, 5, 6, 8, 9 of 10) wordt een punt bepaald en gegooid tot dat punt opnieuw wordt gegooid (winnen) of een 7 wordt gegooid (verliezen)
We berekenen eerst de waarschijnlijkheid dat we winnen voordat we het punt bepalen. De kans om 7 te raken is 6/36 en de kans om 11 te raken is 2/36. Deze twee breuken moeten dan bij elkaar opgeteld worden om 3/36+2/36 = 2/9 = 0,2222 te verkrijgen.
Wij richten onze aandacht nu op de situatie waarin een punt is bepaald. Dat wil zeggen, als het punt 4, 5, 6, 8, 9 of 10 is. Laten we beginnen met een totaal van 4.
Als er een 4 wordt gegooid, wordt er een punt bepaald en gooit de speler door tot er een 4 of 7 wordt gegooid. Dit is waar we het rijk van voorwaardelijke waarschijnlijkheid binnengaan. Dit zegt ons wat de kans op gebeurtenis A is als gebeurtenis B zich op hetzelfde moment voordoet. In ons geval zal het zijn wat de kans is dat we winnen (gooit een 4) als de ronde eindigt (gooit een 4 of een 7). Deze waarden worden vervolgens in de formule ingevoerd:
- P(A) = Vallen som van 4: 3/36
- P(A∩B) = na aanpassingen vinden we dat het gelijk is aan A
- P(B) = val 4 of 7: 3/36 + 6/36 = 9/36
Daaruit volgt dat:
- P(4|4 of 7) = (3/36)/(9/36) = 1/3
Op dezelfde manier kunnen we de sommen van 5, 6, 8, 9 en 10 berekenen
- P(5|5 of 7) = (4/36)/(10/36) = 2/5
- P(6|6 of 7) = (5/36)/(11/36) = 5/11
- P(8|8 of 7) = (5/36)/(11/36) = 5/11
- P(9|9 of 7) = (4/36)/(10/36) = 2/5
- P(10|10 of 7) = (3/36)/(9/36) = 1/3
Nu kunnen we de winkans berekenen als de kans op de oorspronkelijke worp toen het punt werd bepaald en de volgende worp toen de speler won.
- Originele worp 4 x P(4|4 of 7) = 3/36 x 1/3 = 1/36
- Originele worp 5 x P(5|5 of 7) = 4/36 x 2/5 = 2/45
- Originele worp 6 x P(6|6 of 7) = 5/36 x 5/11 = 25/396
- Originele worp 8 x P(8|8 of 7) = 5/36 x 5/11 = 25/396
- Originele worp 9 x P(9|9 of 7) = 4/36 x 2/5 = 2/45
- Originele worp 10 x P(10|10 of 7) = 3/36 x 1/3 = 1/36
Al deze breuken geven ons de kans om te winnen als de eerste worp 4, 5, 6, 8, 9 of 10 is. Als u de totale waarschijnlijkheid wilt weten om te winnen op een Pass line bet, moet u ze allemaal optellen en de kans om te winnen voor het punt (gooit een 7 of 11 - 2/9) toevoegen.
2/9 + 1/36 + 2/45 + 25/396 + 25/396 + 2/45 + 1/36 = 244/495
Omdat 244/495 precies 49,3% is. Dat is iets minder dan 50%. In feite zult u waarschijnlijk geen betere kans vinden om te winnen met een 1 op 1 uitbetaling. Behalve misschien blackjack, als je kaarten kunt tellen.
Waarschijnlijkheid van Blackjack
Blackjack is het kansspel waarbij de kansen het belangrijkst zijn. Bij blackjack kun je het huisvoordeel beïnvloeden met je vaardigheid en kennis. Je hoeft alleen maar de optimale strategie hiervoor te kennen, en als je weet hoe je kaarten moet tellen, zul je zelfs met het voordeel van de speler spelen. Rond en rond hoef je eigenlijk niet alle specifieke waarschijnlijkheden te kennen, omdat al deze berekeningen reeds gedaan zijn door wiskundigen vóór jou, die alle tactieken en strategieën voor blackjack bedacht hebben.
Omwille van de interesse zullen we echter tonen hoe de kans berekend kan worden voor enkele belangrijke fenomenen bij blackjack.
Als we het probleem van de waarschijnlijkheid bekijken vanuit het perspectief van een spel kaarten, is het duidelijk dat het aantal mogelijke uitkomsten snel toeneemt. Blackjack wordt gespeeld met een kaartspel van 52 kaarten, 4 kleuren en 13 waarden. Dit geeft de volgende kansen:
- Ik trek een Aas uit het spel (of een individuele kaart): 4/52=0.0769 (7.69%)
- Ik trek een schoppen uit de stapel: 13/52=0.25 (25%)
In tegenstelling tot bijvoorbeeld het opgooien van een munt, roulette of een gokautomaat, heeft een kaartspel echter een soort "geheugen". Of beter gezegd, het betekent dat eerdere resultaten een effect hebben op huidige en toekomstige zetten. Dit is te wijten aan het feit dat er een kaart van de stapel is gevallen en dit verandert de beginsituatie. Laten we eens kijken naar een voorbeeld waarbij de eerste kaart die getrokken wordt uit een spel van 52 kaarten een Aas is (7,69% kans). De waarschijnlijkheid dat een Aas opnieuw wordt getrokken als tweede kaart van het kaartspel zal nu anders zijn. Na de eerste trekking is het aantal azen gedaald tot 3 en het aantal kaarten tot 51.
Waarschijnlijkheid voor blackjack natuurlijk
Waar iedere speler als eerste in geïnteresseerd zal zijn, is de waarschijnlijkheid van blackjack. Dat wil zeggen, wat zijn de kansen dat een speler een aas en een tienkaart krijgt aan het begin van de ronde - met andere woorden, een natural.
Deze situatie kan zich op twee manieren voordoen, en als we de twee manieren optellen, krijgen we onze kansen op blackjack:
Opmerking: We tellen voor single deck blackjack. Dus 52 kaarten, 4 azen en 16 tienen. De kaart van de dealer is niet zichtbaar, dus zal het de kans niet beïnvloeden.
- De speler ontvangt de eerste aas en een tien kaart
De speler krijgt de eerste Aas-kaart met kans 4/52. De speler moet dus de tweede kaart met een tien krijgen, en daarvoor zijn de kansen 16/51. Deze twee kansen moeten met elkaar worden vermenigvuldigd om 16/663 te krijgen.
- De speler krijgt de eerste tien kaart en een aas
De kans dat een speler de eerste kaart met waarde 10 krijgt is 16/52. De kans dat een speler daarna een aas krijgt is 4/51. Na vermenigvuldiging krijgen we 16/663.
Als we de kans op blackjack willen weten, tellen we deze twee verschijnselen gewoon op. Dus 16/663 + 16/663 = 32/663 = 4,827%. Met andere woorden, een speler krijgt ongeveer eens in de 20 handen een blackjack. U kunt de kans voor multi-deck tafels op een gelijkaardige manier berekenen, wat wij reeds voor u hebben gedaan.
|
Aantal pakketten |
Waarschijnlijkheid |
|
1 |
4,827 % |
|
2 |
4,780 % |
|
3 |
4,764 % |
|
4 |
4,757 % |
|
5 |
4,752 % |
|
6 |
4,749 % |
Waarschijnlijkheid voor buste
Het kan ook interessant zijn om te weten wat je kansen zijn op een bust. Nogmaals, we zullen ons concentreren op een voorbeeldsituatie waarin je speelt met alleen de dealer aan een single deck tafel. Laten we eens kijken naar een zeer eenvoudige situatie waarin een speler 2 kaarten heeft met een waarde van 10 in totaal, zodat hij 20 punten heeft. In een situatie waarin de speler een derde kaart krijgt, zijn er al 3 kaarten van de stapel gespeeld. Dan blijven er 49 kaarten over in de stapel. Van deze 49 kaarten, zullen slechts 4 azen je helpen. Van deze 49, zijn 45 kaarten ongewenst. De kans op een bust is dus 45/49=0,9183673.
Je kunt andere kansen op een vergelijkbare manier berekenen. Je moet je de situatie altijd goed kunnen voorstellen. Dat is alles.
|
Waarde van de hand |
Waarschijnlijkheid van bustes |
|
21 |
100 % |
|
20 |
92 % |
|
19 |
85 % |
|
18 |
77 % |
|
17 |
69 % |
|
16 |
62 % |
|
15 |
58 % |
|
14 |
56 % |
|
13 |
39 % |
|
12 |
31 % |
|
11 minder |
0 % |
Laten we nu eens kijken hoe groot de kans is dat de dealer bust gaat voor elke kaart.
|
Waarde van de hand |
Waarschijnlijkheid van bustes |
|
2 |
35,30 % |
|
3 |
37,56 % |
|
4 |
40,28 % |
|
5 |
42,89 % |
|
6 |
42,08 % |
|
7 |
25,99 % |
|
8 |
23,86 % |
|
9 |
23,34 % |
|
10, J, Q, K |
21,43 % |
|
Ace |
11,65 % |
Waarschijnlijkheid van poker
Poker is een ander kaartspel waarbij kansberekening uiterst belangrijk is. Onder andere. Dus laten we eens kijken wat je kansen zijn bij poker.
Pre-flop waarschijnlijkheid
Nu we geschetst hebben hoe kansberekening werkt in een kaartspel, kunnen we overgaan tot praktische toepassingen. Allereerst zullen we laten zien hoe je de kans berekent dat je geen paren meer hebt in een hand. (bijvoorbeeld, de veelbesproken Aces). In dit geval moeten we de kansen met elkaar vermenigvuldigen.
(4/52) x (3/51) = (12/2652) = (1/221) = 0,004524 (0,45 %)
Opmerking: Als je poker speelt in een casino dat ongeveer 30 handen per uur uitdeelt, krijg je ongeveer eens in de 7 en een half uur een paar azen.
Wat zijn de kansen om een van de 13 mogelijke paren te krijgen als je deelt? We kunnen aannemen dat de kansen 1/221 per individueel paar zijn (zie bovenstaande formule). Er kunnen in totaal 13 van deze paren zijn, dus de formule voor de berekening wordt 13/221=0,0588. Je kunt dus ongeveer om de 35 wedstrijden een paar verwachten.
Waarschijnlijkheid in poker speler tegen speler
Poker is echter een spel voor meerdere spelers, dat meestal tegen elkaar wordt gespeeld. Dus hier is een selectie van de meest voorkomende pre-flop situaties.
|
Je hand. |
Hand van je tegenstander |
Waarschijnlijkheid van winnen |
|
Hoog paar |
Twee lage kaarten |
83 % |
|
Hoog paar |
Laag paar |
82 % |
|
Midden paar |
Hoge, lage kaart |
71 % |
|
Twee hoge kaarten |
Twee lage kaarten |
63 % |
|
Twee hoge kaarten |
Laag paar |
55 % |
Berekening van de waarschijnlijkheid door "outs"
Als het je lukt om de kaarten op de flop te zien, zul je zeker verder geïnteresseerd zijn in wat je kansen zijn om je hand te verbeteren. In dit geval zullen we het hebben over de zogenaamde "outs". In poker verwijst deze term naar alle kaarten die je kunnen helpen. Zo'n veel voorkomend geval kan zijn wanneer een speler twee kaarten in een kleur heeft en er nog twee kaarten van dezelfde kleur op de flop verschijnen. De speler heeft dan 4 kaarten om te flushen en heeft dus 9 outs, waardoor er 9 kaarten overblijven om een flush te vormen.
|
Aantal uitjes |
Flop - Turn |
Turn - River |
Draai een rivier |
|
20 |
42,6 % |
43,5 % |
67,5 % |
|
19 |
40,4 % |
41,3 % |
65,0 % |
|
18 |
38,3 % |
39,1 % |
62,4 % |
|
17 |
36,2 % |
37,0 % |
59,8 % |
|
16 |
34,0 % |
34,8 % |
57,0 % |
|
15 |
31,9 % |
32,6 % |
54,1 % |
|
14 |
29,8 % |
30,4 % |
51,2 % |
|
13 |
27,7 % |
28,3 % |
48,1 % |
|
12 |
25,5 % |
26,1 % |
45,0 % |
|
11 |
23,4 % |
23,9 % |
41,7 % |
|
10 |
21,3 % |
21,7 % |
38,4 % |
|
9 |
19,1 % |
19,6 % |
35,0 % |
|
8 |
17,0 % |
17,4 % |
31,5 % |
|
7 |
14,9 % |
15,2 % |
27,8 % |
|
6 |
12,8 % |
13,0 % |
24,1 % |
|
5 |
10,6 % |
10,9 % |
20,3 % |
|
4 |
8,5 % |
8,7 % |
16,5 % |
|
3 |
6,4 % |
6,5 % |
12,5 % |
|
2 |
4,3 % |
4,3 % |
8,4 % |
|
1 |
2,1 % |
2,2 % |
4,3 % |
Opmerking: Er is een zeer gemakkelijke methode om de kans op outs te berekenen, zodat je het direct aan de tafel kunt doen. Dit wordt over het algemeen de "vier en twee"-regel genoemd. Na de flop vermenigvuldigt de speler gewoon het aantal outs met 4 om de kans op de turn en river te bepalen. Als hij geen kaart krijgt bij de turn, vermenigvuldigt hij gewoon het aantal outs met twee om de waarschijnlijkheid te berekenen dat hij de kaart bij de river krijgt.
We kunnen opnieuw het voorbeeld gebruiken van 4 kaarten van dezelfde kleur na de flop. Je outs zijn dus 9 kaarten en de kans op een flush na de turn en river is 36% (9x4). Laten we zeggen dat je geen kaart krijgt als je aan de beurt bent. In dat geval vermenigvuldigen we de outs met twee en vinden we dat we een kans van 18% (9x2) hebben dat we geen kaarten meer hebben in de kleur bij de river. Zoals u aan de hand van de tabel kunt zien, is deze methode heel eenvoudig, maar aan de andere kant onnauwkeurig, maar zij kan worden toegepast.

 NL
NL  English
English  čeština
čeština  Polski
Polski  Slovenčina
Slovenčina  Русский
Русский  Deutsch
Deutsch  Slovenski
Slovenski  Svenska
Svenska  Português
Português  Italiano
Italiano  Español
Español  Français
Français  Suomalainen
Suomalainen  Български
Български  Românesc
Românesc  Magyar
Magyar  Eesti
Eesti  Ελληνική
Ελληνική  Latviešu
Latviešu  Lietuvių
Lietuvių  やまと
やまと  中国
中国  Dansk
Dansk  Türkçe
Türkçe  ID
ID  Українська
Українська  한국어
한국어  Norsk
Norsk 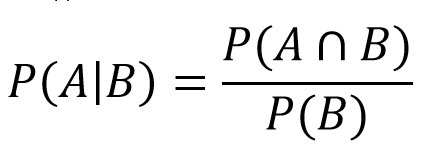


U moet ingelogd zijn om een opmerking toe te voegen