Ймовірність та ігри в казино
 Peter Sommer
Peter Sommer
Чи розумієте ви свої шанси? Якщо ви збираєтеся грати в казино, ви повинні переконатися, що знаєте свої шанси і розумієте їх досконало. Чому? Тому що ймовірність - це двигун, який змушує казино працювати. Без ймовірності гральна індустрія була б неможливою.
Шанс - це просто ймовірність того, що щось станеться. Ймовірність є частиною нашого повсякденного життя. Коли ми вирішуємо перейти жваву вулицю на червоне світло, є певна ймовірність, що нас зіб'є машина, але натомість у нас є шанс перейти вулицю швидше і виграти трохи часу.
Коли ми граємо в азартні ігри, ми оцінюємо ймовірність настання певної події, щоб сформулювати свою ставку. Саме в таких випадках ми обчислюємо ймовірність.
Приклад з ймовірністю
Припустимо, у нас є мішок з чотирма кульками, з яких лише одна червона, а інші три сині. Ймовірність витягнути червону кульку, не дивлячись, становить 1 до 4.
Існує кілька способів виразити ймовірність. Можна також сказати, що проти червоного є шанс 3 до 1, тому що в середньому ми витягуємо три сині кульки за кожну витягнуту червону кульку.
Ми також можемо виразити наші шанси у відсотках, тобто наша ймовірність витягнути червону кульку дорівнює 25%, якщо ймовірність витягнути кульку 100%. Отже, 100 ділимо на чотири і отримуємо 25%.
Ймовірність випадання синьої кулі дорівнює 75%, якщо є три сині кулі з ймовірністю випадання 25%.
Імовірність ігор у казино
Казино працює за принципом пропонування коефіцієнтів, які не такі вже й хороші, враховуючи наш довгостроковий результат.
Приклад з мішком повітряних кульок - простий спосіб показати, як працює казино. Припустимо, казино пропонує коефіцієнт 3 на випадання червоної кульки. Якщо ви поставите $5, то в середньому за чотири спроби ви витягнете синю кульку 3 рази і програєте $15, а на четвертий раз витягнете червону кульку і виграєте $10, але казино все одно залишиться в плюсі на $5. Всі азартні ігри засновані на ймовірності. Про це вам скаже будь-який досвідчений гемблер. Тому важливо знати ці цифри і вміти з ними працювати. Тому зараз ми покажемо вам, як обчислювати ймовірність в азартних іграх. Якщо ви правильно зрозуміли принцип, ви можете використовувати його для обчислення ймовірності будь-чого іншого.
Ймовірність в рулетці
Рулетка - це як колесо фортуни. І знаєте чому? Для пояснення потрібно лише 3 слова - Теорія великих чисел. Кожна людина, яка керує казино або виробляє ігри для онлайн-казино, дуже добре знає цю теорію. Тому що це безпосередньо пов'язано з його заробітком. І завдяки цьому казино завжди виграє у гравців у довгостроковій перспективі. Все пов'язано з ймовірністю і краєм будинку.
Примітка: Всі номери в статті відносяться до європейської рулетки - таким чином, ми нарахували 37 номерів.
Як записати ймовірність
Існує кілька способів написання ймовірності. Напевно, найвідоміший - це відсотки. Крім того, використовуються вирази з дробом або відношенням.
- Виражено у відсотках (%) - тут мало що можна додати, але для повноти картини, це відсоток для обраної події. Він розраховується як (Частина/Загальна сума)*100. Наприклад, ймовірність випадання обраного числа на колесі рулетки (Straight): 1/37*100=2,7%.
- Вираз через дріб (1/x) - При вираженні ймовірності через дріб, ми говоримо, що явище відбувається 1 раз з X випробувань. У числовому вираженні ми покладаємося на обчислення відсотків. Якщо розглянути приклад 1/37 вище, це означає, що статистично вибране число на колесі рулетки випаде 1 раз за 37 обертань.
- Вираз співвідношенням (x до 1) - кожного разу, коли відбувається X, вибране явище відбувається 1 раз. Тут ми знову дотримуємося ймовірності для обраного числа в рулетці. У цьому випадку співвідношення буде записано як 36 до 1. Це означає, що після кожних 36 обертань, де число не випало, буде один випадок, коли вибране число випаде.
Примітка: Як говорить теорія великих чисел, ймовірність - це, по суті, математична межа. З кожним наступним випробуванням ви реально наближаєтесь до розрахованого результату.
Як бачите, вирази з використанням дробів і з використанням коефіцієнтів дуже схожі. Різниця полягає лише в тому, що дріб рахує всі обертання, а коефіцієнт ділить загальну кількість обертань на дві категорії.
Таблиця ймовірностей для окремих ставок у рулетці
|
Ставлю |
Витяг з |
Співвідношення |
У відсотках |
|
Пряма ставка |
1/2,055 |
1.055 до 1 |
48,6 % |
|
Колонка |
1/3,08 |
2,08 до 1 |
32,4 % |
|
Дюжина |
1/3,08 |
2,08 до 1 |
32,4 % |
|
Шоста лінія |
1/6,17 |
5.17 до 1 |
16,2 % |
|
Куточок |
1/9,25 |
8,25 до 1 |
10,8 % |
|
Вулиця |
1/12,33 |
11.33 до 1 |
8,1 % |
|
Спліт |
1/19,5 |
18,5 до 1 |
5,4 % |
|
Прямо. |
1/37 |
36 до 1 |
2,7 % |
Імовірність для прямої ставки
Цікавим також може бути математичне порівняння для повторення обраного явища. Для цього випадку ми вибрали пряму ставку, а саме, наприклад, ставку на червоне. Отже, як зміниться ймовірність того, що червоний колір випаде, наприклад, 5 разів поспіль?
|
Кількість обертань |
Співвідношення |
У відсотках |
|
1 |
1,06 до 1 |
48,6 % |
|
2 |
3,23 до 1 |
23,7 % |
|
3 |
7,69 до 1 |
11,5 % |
|
4 |
16,9 до 1 |
5,6 % |
|
5 |
35,7 до 1 |
2,73 % |
|
6 |
74,4 до 1 |
1,33 % |
|
7 |
154 до 1 |
0,65 % |
|
8 |
318 до 1 |
0,31 % |
|
9 |
654 до 1 |
0,15 % |
|
10 |
1 346 до 1 |
0,074 % |
|
15 |
49 423 до 1 |
0,002 % |
|
20 |
1 813 778 до 1 |
0,000055 % |
Як бачимо, зі збільшенням кількості обертань ймовірність цього явища стрімко зменшується. Однак майте на увазі, що ці ймовірності описують явище в цілому. Генератор випадкових чисел не враховує попередні результати, тому навіть якщо серія ігор, в якій червоний колір випадає 20 разів поспіль, трапляється раз на 1.813 мільйонів ігор, 21-й раунд матиме таке ж перевагу і ймовірність (тобто 48.6%), як і всі інші раунди гри.
Часто в цьому випадку можна зустріти термін "помилка гравця", коли гравець вважає, що якщо один колір випадає кілька разів поспіль, то існує більша ймовірність того, що інший колір випаде в наступному обертанні. Насправді це не так. Найвідоміший випадок цієї помилки спостерігався в 1913 році в казино Монте-Карло, коли на колесі рулетки 26 разів поспіль випало чорне, і майже протягом усієї цієї неймовірної смуги, і навіть після її закінчення, люди несамовито ставили на червоне. Тоді казино заробило дуже непогані гроші.
Примітка: Ймовірність того, що колір випаде 26 разів поспіль, становить 0,000000730870% і трапляється один раз на 67 мільйонів ігор.
Як розрахувати ймовірність рулетки
Хочете дізнатися більше коефіцієнтів для окремих ставок? Спробуйте порахувати їх самостійно. Робота з відсотками та ймовірностями не дуже складна. Як правило, найпростіший спосіб - почати з дробів і використовувати їх для обчислення подальших відсотків і співвідношень. Наприклад, якщо ви хочете обчислити ймовірність у вигляді дробу для ситуації, коли червоний колір є червоним, зробіть наступне:
Загальна кількість червоних на ігровому полі/Загальна кількість ігрових полів = 18/37
Ймовірність для одного обертання
Знову ж таки, тут діє просте правило. Просто підрахуйте кількість полів, які принесуть вам виграш, і розділіть її на загальну кількість полів.
Наприклад:
- Колір - 18/37
- Суда/Ліча - 18/37
- Дюжина - 12/37
- Номер 0 - 1/37
- Чорні та парні - 9/37 (на ігровому полі є лише 9 чисел, які є одночасно чорними та парними)
- Дюжина та стовпчик - 4/37 (у дюжині та стовпчику лише по 4 числа)
Так само, як і ймовірність виграшу, ви можете розрахувати ймовірність програшу. Просто підрахуйте кількість полів, що не виграли, і знову розділіть їх на загальну кількість полів. Наприклад, ймовірність програшу, якщо ви поставите на червоне, становить 19/37 (18 чорних полів + зелене зеро).
Примітка: Щоб звести дріб до 1/x, просто розділіть чисельник і знаменник на чисельник. Наприклад, 18/37 (ви ділите обидва числа на 18) стане 1/2.055 після коригування. Це означає, що на кожні 2.055 ходів один хід призведе до червоного або чорного кольору.
Імовірність для декількох обертань
Після того, як ви освоїте розрахунок для одиночних обертань, розрахунок ймовірності для множинних обертань буде дуже простим. Просто помножте окремі частки одна на одну.
Приклади:
- обертання - ставка на червоне = 18/37
- обертання - ставка на дюжину = 12/37
Ймовірність виграшу в обох раундах = (18/37)*(12/37)=1/6.34 або 15.77% або 5.34 до 1
- обертання - пряма ставка - 1/37
- обертання - пряма ставка - 1/37
Ймовірність виграшу в обох раундах = (1/37)*(1*37)=1/1369 або 0,073% або 1368 до 1
- обертання - ставка на чорне та непарне 9/37
- обертання - ставка на парне 18/37
- обертання - ставка на стовпчик 12/37
Ймовірність виграти всі 3 раунди = (9/37)*(18/37)*(12/37)=1/26.06 або 3.84% або 25.06 до 1
Фактичне перетворення між записами знову ж таки дуже просте. Ви отримуєте відсотки, розділивши дріб у вигляді 1/x, а потім помноживши на 100. Ви отримуєте пропорційний запис у вигляді X до 1, віднімаючи 1 від знаменника, який є виграшним раундом від загальної суми. Дивіться приклади вище в цьому параграфі.
Ймовірність випадання кубиків
Кості - ще одна азартна гра, в якій відносно легко розрахувати шанси. Перш ніж ми перейдемо до розрахунку шансів на виграш у крепсі, давайте подивимося на ймовірність самих випадінь гральних кісток.
Кубики мають 6 граней. Таким чином, ймовірність того, що випаде будь-яке число, дорівнює 1/6. У кості традиційно грають двома гральними кістками. Таким чином, ймовірність того, що будь-які два числа з'єднаються, дорівнює 2/36. Однак нас цікавлять не стільки конкретні числа, скільки сума цих чисел, що в крепсі набагато важливіше. Знову ж таки, ми будемо використовувати формулу: кількість виграшних комбінацій/кількість усіх комбінацій.
Припустимо, ми хочемо дізнатися ймовірність для суми 7. Виграшні комбінації: (1-6), (2-4), (3-3), (4-2), (6-1). Як бачите, всього існує 6 різних комбінацій, в яких на двох гральних кістках може випасти сума 7. А оскільки кількість усіх комбінацій дорівнює 36, то ймовірність появи 7 дорівнює 6/36=0.1666
Таким чином, можна легко розрахувати всі інші можливі результати.
|
Всього |
Ймовірність |
|
2 |
1/36 |
|
3 |
2/36 |
|
4 |
3/36 |
|
5 |
4/36 |
|
6 |
5/36 |
|
7 |
6/36 |
|
8 |
5/36 |
|
9 |
4/36 |
|
10 |
3/36 |
|
11 |
2/36 |
|
12 |
1/36 |
Шанси на виграш у кості
Коротко розглянемо правила гри в кості. Найпоширеніша ставка - це лінія "Прохід".
- Якщо випадає 7 або 11, ви виграєте
- Якщо випадає 2, 3 або 12, ви програєте
- В інших випадках (4, 5, 6, 8, 9 або 10) визначається очко і продовжує випадати до тих пір, поки не випаде знову (виграш) або поки не випаде 7 (програш)
Перед тим, як визначити точку, ми спочатку обчислюємо ймовірність виграшу. Ймовірність випадання 7 дорівнює 6/36, а ймовірність випадання 11 дорівнює 2/36. Потім ці дві частки потрібно скласти разом, щоб отримати 3/36+2/36 = 2/9 = 0,2222.
Тепер звернемо увагу на ситуацію, коли точка визначена. Тобто, коли точка дорівнює 4, 5, 6, 8, 9 або 10. Почнемо з того, що їх всього 4.
Якщо випадає 4, визначається очко, і гравець продовжує кидати до тих пір, поки не випаде 4 або 7. Тут ми вступаємо в область умовної ймовірності. Це показує нам, яка ймовірність події A, якщо подія B відбувається в той самий час. У нашому випадку це буде ймовірність того, що ми виграємо (випаде 4), якщо раунд закінчиться (випаде 4 або 7). Потім ми підставляємо ці значення у формулу:
- P(A) = Сума випадань 4: 3/36
- P(A∩B) = після коригування знаходимо, що дорівнює A
- P(B) = Випадає 4 або 7: 3/36 + 6/36 = 9/36
З цього випливає:
- P(4|4 або 7) = (3/36)/(9/36) = 1/3
Аналогічним чином ми можемо обчислити суми 5, 6, 8, 9 і 10
- P(5|5 або 7) = (4/36)/(10/36) = 2/5
- P(6|6 або 7) = (5/36)/(11/36) = 5/11
- P(8|8 або 7) = (5/36)/(11/36) = 5/11
- P(9|9 або 7) = (4/36)/(10/36) = 2/5
- P(10|10 або 7) = (3/36)/(9/36) = 1/3
Тепер ми можемо обчислити шанс виграшу як ймовірність першого кидка, коли було визначено очко, і наступного кидка, коли гравець виграв.
- Оригінальний рулон 4 x P(4|4 або 7) = 3/36 x 1/3 = 1/36
- Оригінальний рулон 5 x P(5|5 або 7) = 4/36 x 2/5 = 2/45
- Оригінальний рулон 6 x P(6|6 або 7) = 5/36 x 5/11 = 25/396
- Оригінальний рулон 8 x P(8|8 або 7) = 5/36 x 5/11 = 25/396
- Оригінальний рулон 9 x P(9|9 або 7) = 4/36 x 2/5 = 2/45
- Оригінальний рулон 10 x P(10|10 або 7) = 3/36 x 1/3 = 1/36
Всі ці дроби дають нам ймовірність виграшу, якщо при першому кидку випаде 4, 5, 6, 8, 9 або 10. Якщо ви хочете дізнатися загальну ймовірність виграшу за ставкою на лінію "Пас", вам потрібно скласти їх усі і додати шанс виграшу до очка (випадання 7 або 11 - 2/9).
2/9 + 1/36 + 2/45 + 25/396 + 25/396 + 2/45 + 1/36 = 244/495
Тому що 244/495 - це рівно 49,3%. Це трохи менше 50%. Насправді, ви, мабуть, не знайдете кращого шансу на перемогу з виплатою 1 до 1. За винятком, можливо, блекджека, якщо ви вмієте рахувати карти.
Ймовірність гри в блекджек
Блекджек - це азартна гра, в якій шанси мають найбільше значення. У блекджеку ви можете впливати на перевагу будинку за допомогою своїх навичок і знань. Потрібно лише знати оптимальну стратегію для цього, а якщо ви вмієте рахувати карти, то навіть зіграєте з перевагою гравця. Насправді вам не потрібно знати всі конкретні ймовірності, тому що всі ці розрахунки вже були зроблені математиками до вас, які придумали всі тактики і стратегії для блекджека.
Заради інтересу, однак, ми покажемо, як обчислити ймовірність для деяких важливих явищ у блекджеку.
Якщо поглянути на проблему ймовірності з точки зору колоди карт, то зрозуміло, що кількість можливих результатів стрімко зростає. У блекджек грають колодою з 52 карт, 4 мастей і 13 номіналів. Це дає наступні коефіцієнти:
- Я витягую туза з колоди (або будь-яку окрему карту): 4/52=0.0769 (7.69%)
- Тягну піку з колоди: 13/52=0,25 (25%)
Однак, на відміну, наприклад, від підкидання монети, рулетки або ігрових автоматів, колода карт має щось на кшталт "пам'яті". Точніше, це означає, що попередні результати впливають на поточні та майбутні ходи. Це пов'язано з тим, що з колоди була скинута карта, і це змінює стартову ситуацію. Розглянемо приклад, коли туз був витягнутий першою картою з 52-карткової колоди (ймовірність 7,69%). Ймовірність того, що туз знову буде витягнутий другою картою з колоди, тепер буде іншою. Після першого розіграшу кількість тузів зменшилася до 3, а кількість карт - до 51.
Ймовірність для блекджека натуральна
Перше, що цікавить кожного гравця, - це ймовірність випадання блекджека. Тобто, які шанси, що гравець отримає туза і десятку карт на самому початку раунду - іншими словами, натурал.
Така ситуація може виникнути двома способами, і якщо ми додамо ці два способи, то отримаємо наші шанси в блекджеку:
Примітка: Ми рахуємо для одноколодного блекджека. Отже, 52 карти, 4 тузи і 16 десяток. Карту дилера не видно, тому вона не впливає на ймовірність.
- Гравець отримує перший туз і десятку карт
З ймовірністю 4/52 гравець отримує першу карту Туза. Отже, гравець повинен отримати другу карту з десяткою, і для цього шанси становлять 16/51. Ці дві ймовірності потрібно помножити одна на одну, щоб отримати 16/663.
- Гравець отримує перші десять карт і туза
Ймовірність того, що гравець отримає першу карту зі значенням 10, дорівнює 16/52. Шанси гравця отримати туза після цього становлять 4/51. Після множення отримуємо 16/663.
Якщо ми хочемо дізнатися ймовірність випадання блекджека, нам просто потрібно додати ці два явища. Отже, 16/663 + 16/663 = 32/663 = 4,827%. Іншими словами, гравець отримує блекджек приблизно раз на 20 роздач. Ви можете розрахувати ймовірність для багатоколодних столів аналогічним чином, що ми вже зробили для вас.
|
Кількість пакунків |
Ймовірність |
|
1 |
4,827 % |
|
2 |
4,780 % |
|
3 |
4,764 % |
|
4 |
4,757 % |
|
5 |
4,752 % |
|
6 |
4,749 % |
Ймовірність обриву
Також може бути цікаво дізнатися, які у вас шанси на невдачу. Знову ж таки, ми зосередимося на прикладі ситуації, коли ви граєте тільки з дилером за столом з однією колодою. Давайте розглянемо дуже просту ситуацію, коли у гравця є 2 карти з сумарною вартістю 10, і він має 20 очок. У ситуації, коли гравець отримує третю карту, 3 карти з колоди вже були зіграні. У колоді залишається 49 карт. З цих 49 карт вам допоможуть лише 4 тузи. З цих 49 карток 45 є небажаними. Таким чином, ймовірність того, що ви потрапите в халепу, дорівнює 45/49=0.9183673.
Ви можете обчислити інші ймовірності подібним чином. Завжди потрібно вміти правильно уявляти собі ситуацію. Це все.
|
Значення руки |
Ймовірність помилок |
|
21 |
100 % |
|
20 |
92 % |
|
19 |
85 % |
|
18 |
77 % |
|
17 |
69 % |
|
16 |
62 % |
|
15 |
58 % |
|
14 |
56 % |
|
13 |
39 % |
|
12 |
31 % |
|
На 11 менше |
0 % |
Тепер давайте подивимося, наскільки ймовірно, що дилер поб'є кожну карту.
|
Значення руки |
Ймовірність помилок |
|
2 |
35,30 % |
|
3 |
37,56 % |
|
4 |
40,28 % |
|
5 |
42,89 % |
|
6 |
42,08 % |
|
7 |
25,99 % |
|
8 |
23,86 % |
|
9 |
23,34 % |
|
10, J, Q, K |
21,43 % |
|
Туз. |
11,65 % |
Імовірність покеру
Покер - ще одна карткова гра, де ймовірність надзвичайно важлива. Серед іншого. Отже, давайте подивимося, які ваші шанси в покері.
Імовірність префлопу
Тепер, коли ми з'ясували, як працює ймовірність у колоді карт, давайте перейдемо до практичного застосування. Перш за все, ми покажемо вам, як розрахувати ймовірність того, що у вас закінчиться пара (наприклад, тузи, про які так багато говорять). У цьому випадку нам потрібно помножити ймовірності одна на одну.
(4/52) x (3/51) = (12/2652) = (1/221) = 0,004524 (0,45 %)
Примітка: Якщо ви граєте в покер в казино, де роздають близько 30 роздач на годину, ви будете отримувати пару тузів приблизно раз на 7 з половиною годин гри.
Отже, які шанси отримати будь-яку з 13 можливих пар під час роздачі? Ми можемо припустити, що шанси становлять 1/221 на кожну пару (див. формулу вище). Всього таких пар може бути 13, тому формула для розрахунку буде 13/221=0,0588. Отже, ви можете очікувати пару приблизно раз на 35 ігор.
Ймовірність в покері гравець проти гравця
Однак покер - це багатокористувацька гра, в яку зазвичай грають один проти одного. Отже, ось добірка найпоширеніших ситуацій на префлопі.
|
Твоя рука |
Рука вашого опонента |
Ймовірність виграшу |
|
Старша пара |
Дві низькі карти |
83 % |
|
Старша пара |
Нижня пара |
82 % |
|
Середня пара |
Висока, низька карта |
71 % |
|
Дві високі карти |
Дві низькі карти |
63 % |
|
Дві високі карти |
Нижня пара |
55 % |
Розрахунок ймовірності за "аутами"
Якщо вам вдасться побачити карти на флопі, ви неодмінно зацікавитесь, які у вас шанси покращити свою руку. В даному випадку мова піде про так звані "аути". У покері цим терміном позначають будь-які карти, які можуть вам допомогти. Поширеним випадком може бути ситуація, коли у гравця на руках дві карти однієї масті, а на флопі з'являються ще дві карти тієї ж масті. Після цього у гравця залишається 4 карти для флеша і, таким чином, він має 9 аутів, залишаючи 9 карт, з якими можна сформувати флеш.
|
Кількість аутів |
Флоп - Терн |
Терн - Рівер |
"Поверніть річку |
|
20 |
42,6 % |
43,5 % |
67,5 % |
|
19 |
40,4 % |
41,3 % |
65,0 % |
|
18 |
38,3 % |
39,1 % |
62,4 % |
|
17 |
36,2 % |
37,0 % |
59,8 % |
|
16 |
34,0 % |
34,8 % |
57,0 % |
|
15 |
31,9 % |
32,6 % |
54,1 % |
|
14 |
29,8 % |
30,4 % |
51,2 % |
|
13 |
27,7 % |
28,3 % |
48,1 % |
|
12 |
25,5 % |
26,1 % |
45,0 % |
|
11 |
23,4 % |
23,9 % |
41,7 % |
|
10 |
21,3 % |
21,7 % |
38,4 % |
|
9 |
19,1 % |
19,6 % |
35,0 % |
|
8 |
17,0 % |
17,4 % |
31,5 % |
|
7 |
14,9 % |
15,2 % |
27,8 % |
|
6 |
12,8 % |
13,0 % |
24,1 % |
|
5 |
10,6 % |
10,9 % |
20,3 % |
|
4 |
8,5 % |
8,7 % |
16,5 % |
|
3 |
6,4 % |
6,5 % |
12,5 % |
|
2 |
4,3 % |
4,3 % |
8,4 % |
|
1 |
2,1 % |
2,2 % |
4,3 % |
Примітка: Існує дуже простий метод розрахунку ймовірності аутів, який дозволяє робити розрахунки прямо за столом. Його зазвичай називають правилом "чотири і два". Після флопу гравець просто множить кількість аутів на 4, щоб знайти ймовірність для терну і ріверу. Якщо він не отримує карту на терні, він просто множить кількість аутів на два, щоб отримати приблизну ймовірність отримати карту на рівері.
Знову ж таки, ми можемо використовувати приклад з 4 картами однієї масті після флопу. Отже, ваші аути складають 9 карт, а ймовірність флеша після терну і ріверу становить 36% (9х4). Припустимо, ви не отримали карту на ходу. У такому випадку ми множимо аути на два і отримуємо, що у нас є 18% (9х2) шансів, що на рівері у нас закінчаться карти в одній масті. Як ви можете бачити, порівнюючи таблицю, цей метод дійсно простий, але з іншого боку неточний, але його можна використовувати.

 UK
UK  English
English  čeština
čeština  Polski
Polski  Slovenčina
Slovenčina  Русский
Русский  Deutsch
Deutsch  Slovenski
Slovenski  Dutch
Dutch  Svenska
Svenska  Português
Português  Italiano
Italiano  Español
Español  Français
Français  Suomalainen
Suomalainen  Български
Български  Românesc
Românesc  Magyar
Magyar  Eesti
Eesti  Ελληνική
Ελληνική  Latviešu
Latviešu  Lietuvių
Lietuvių  やまと
やまと  中国
中国  Dansk
Dansk  Türkçe
Türkçe  ID
ID  한국어
한국어  Norsk
Norsk 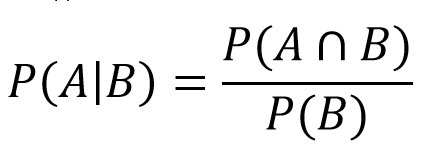


Ви повинні бути авторизовані, щоб додати коментар