Quante probabilità ci sono di vincere al Casinò
 Peter Sommer
Peter Sommer
Capite le vostre possibilità? Se hai intenzione di giocare in un casinò, dovresti assicurarti di conoscere le tue possibilità e capirle perfettamente. Perché? Perché la probabilità è il motore che fa funzionare i casinò. Senza probabilità, l'industria del gioco non sarebbe possibile.
Il caso è semplicemente la probabilità che qualcosa accada. La probabilità fa parte della nostra vita quotidiana. Quando decidiamo di attraversare una strada trafficata con il semaforo rosso, c'è una certa possibilità di essere investiti da un'auto, ma in cambio abbiamo la possibilità di attraversare la strada più velocemente e guadagnare un po' di tempo.
Quando giochiamo d'azzardo, stimiamo la probabilità che un certo evento accada per formulare la nostra scommessa. È in questi casi che calcoliamo la probabilità.
💡 Esempio di probabilità
Diciamo che abbiamo un sacchetto contenente quattro palline di cui solo una è rossa e le altre tre sono blu. La probabilità di estrarre solo la palla rossa senza guardare è 1 su 4.
Ci sono diversi modi per esprimere la probabilità. Possiamo anche dire che c'è una probabilità di 3 su 1 contro il rosso, perché in media si pescano tre palline blu per ogni pallina rossa pescata.
Possiamo anche esprimere le nostre probabilità come percentuale, quindi la nostra probabilità di pescare una palla rossa è del 25% se c'è una probabilità del 100% di pescare una palla. Quindi 100 diviso quattro ci dà il 25%.
La probabilità di estrarre una pallina blu è del 75% se ci sono tre palline blu con il 25% di probabilità di estrazione.
Quante probabilità ci sono di vincere al Casinò
Il casinò opera sul principio di offrire quote che non sono così buone considerando il nostro risultato a lungo termine.
L'esempio di un sacchetto di palloncini è un modo semplice per mostrare come funziona un casinò. Diciamo che un casinò offre quote di 3 per estrarre una palla rossa. Se scommetti 5 dollari, allora in media, in quattro tentativi tirerai la tua palla blu 3 volte e perderai 15 dollari, e la quarta volta tirerai la tua palla rossa e vincerai 10 dollari, ma il casinò sarà ancora in attivo di 5 dollari.
Tutto il gioco d'azzardo è solo una questione di probabilità. Qualsiasi giocatore esperto ve lo dirà. È quindi essenziale avere familiarità con questi numeri e sapere come lavorare con essi. Così qui ora vi mostreremo come calcolare la probabilità nel gioco d'azzardo. Se capite bene il principio, potete usarlo per calcolare la probabilità di qualsiasi altra cosa.
Probabilità alla roulette
La roulette è come la ruota della fortuna. E sapete perché? Ci vogliono solo 3 parole per spiegarlo: la teoria dei grandi numeri. Ogni persona che gestisce un casinò o produce giochi di casinò online conosce molto bene questa teoria. Perché è direttamente collegato ai suoi guadagni. E grazie ad esso, il casinò vince sempre sugli scommettitori anche alla lunga. Tutto è legato alla probabilità e al margine della casa.
📌 Nota: Tutti i numeri nell'articolo si riferiscono alla Roulette Europea - quindi contiamo 37 numeri.
Come scrivere la probabilità
Ci sono diversi modi di scrivere la probabilità. Probabilmente il più noto è quello delle percentuali. Oltre a queste, si usano espressioni che utilizzano una frazione o un rapporto.
- Espresso in percentuale (%) - non c'è molto da aggiungere qui, ma solo per completezza, questa è la percentuale per l'evento selezionato. Si calcola come (Parte/Totale)*100. Per esempio, la probabilità di colpire il numero selezionato su una ruota della roulette (Straight): 1/37*100=2.7%
- Espressione con frazioni (1/x) - Quando si esprime la probabilità usando una frazione, si dice che il fenomeno si verifica 1 volta su X prove. Nell'espressione numerica, ci basiamo sul calcolo delle percentuali. Se consideriamo l'esempio 1/37 di cui sopra, questo significa che un numero selezionato statisticamente sulla ruota della roulette cadrà 1 volta in 37 giri.
- Espressione per rapporto (x a 1) - Ogni volta che si verifica X, il fenomeno selezionato si verifica 1 volta. Anche qui ci atteniamo alla probabilità del numero selezionato alla roulette. In questo caso, il rapporto sarà scritto come 36 a 1. Questo significa che dopo ogni 36 giri in cui il numero non cade, ci sarà un caso in cui il numero selezionato cade.
📌 Nota: come dice la teoria dei grandi numeri, la probabilità è essenzialmente un limite matematico. Con sempre più prove, ci si avvicina realisticamente sempre di più al risultato calcolato.
Come potete vedere, le espressioni che usano le frazioni e i rapporti sono molto simili. L'unica differenza è che una frazione conta tutte le rotazioni, mentre un rapporto divide le rotazioni totali in due categorie.
Tabella delle probabilità per le scommesse individuali nella roulette
|
Scommetti |
Tratto da |
Rapporto |
Percentuali |
|
Una scommessa diretta |
1/2,055 |
1,055 a 1 |
48,6 % |
|
Colonna |
1/3,08 |
2,08 a 1 |
32,4 % |
|
La dozzina |
1/3,08 |
2,08 a 1 |
32,4 % |
|
Sei linee |
1/6,17 |
5,17 a 1 |
16,2 % |
|
Angolo |
1/9,25 |
8,25 a 1 |
10,8 % |
|
Via |
1/12,33 |
11,33 a 1 |
8,1 % |
|
Split |
1/19,5 |
18,5 a 1 |
5,4 % |
|
Dritto |
1/37 |
36 a 1 |
2,7 % |
Probabilità per una scommessa diretta
Un confronto matematico per la ripetizione del fenomeno selezionato potrebbe anche essere interessante. Per questo caso abbiamo scelto una scommessa diretta, in particolare per esempio una scommessa sul rosso. Quindi, quale sarà la probabilità di cambiare il rosso 5 volte di seguito, per esempio?
|
Numero di giri |
Rapporto |
Percentuali |
|
1 |
1,06 a 1 |
48,6 % |
|
2 |
3,23 a 1 |
23,7 % |
|
3 |
7,69 a 1 |
11,5 % |
|
4 |
16,9 a 1 |
5,6 % |
|
5 |
35,7 a 1 |
2,73 % |
|
6 |
74,4 a 1 |
1,33 % |
|
7 |
154 a 1 |
0,65 % |
|
8 |
318 a 1 |
0,31 % |
|
9 |
654 a 1 |
0,15 % |
|
10 |
1 346 a 1 |
0,074 % |
|
15 |
49 423 a 1 |
0,002 % |
|
20 |
1 813 778 a 1 |
0,000055 % |
Come si può vedere, all'aumentare del numero di rotazioni, la probabilità di questo fenomeno diminuisce rapidamente. Tuttavia, tenete presente che queste probabilità descrivono il fenomeno nel suo insieme. Il generatore di numeri casuali non tiene conto dei risultati precedenti, quindi anche se una serie di giochi in cui il rosso colpisce 20 volte di fila si verifica una volta ogni 1,813 milioni di giochi, un giro di 21 giochi avrà lo stesso margine della casa e la stessa probabilità (cioè il 48,6%) di ogni altro giro di giochi.
Spesso in questo caso, si può incontrare il termine Player's Fallacy, dove lo scommettitore crede che se un colore viene colpito più volte di seguito, c'è una maggiore probabilità che l'altro colore venga colpito nel giro successivo. In realtà, non è così. Il caso più famoso di questa fallacia fu osservato nel 1913 al Casinò di Monte Carlo, quando il nero cadde 26 volte di fila sulla roulette, e per quasi tutta la durata di questa incredibile striscia, e anche dopo la sua fine, la gente scommise freneticamente sul rosso. È stato allora che il casinò ha fatto dei bei soldi.
📌 Nota: La probabilità che un colore venga colpito 26 volte di seguito è dello 0,000000730870% e si verifica una volta in 67 milioni di partite.
Come calcolare la probabilità della roulette
Vuoi sapere altre quote per le scommesse individuali? Provate a calcolarli voi stessi. Lavorare con le percentuali e le probabilità non è molto complicato. In generale, il modo più semplice è iniziare con le frazioni e usarle per calcolare ulteriori percentuali e rapporti. Per esempio, se volete calcolare la probabilità in una frazione per una situazione in cui il rosso è rosso, fate come segue:
Numero totale di rossi sul campo da gioco/numero totale di campi da gioco = 18/37
Probabilità per un giro
Anche in questo caso, si applica una semplice regola. Calcola semplicemente il numero di campi che ti daranno una vittoria e dividilo per il numero totale di campi.
Per esempio:
- Colore - 18/37
- Sudá/Lichá - 18/37
- Dozzina - 12/37
- Numero 0 - 1/37
- Nero e pari - 9/37 (ci sono solo 9 numeri nel campo di gioco che sono sia neri che pari)
- Dozzina e colonna - 4/37 (ci sono solo 4 numeri in una dozzina e in una colonna)
Proprio come la probabilità di vincere, si può calcolare la probabilità di perdere. Basta contare il numero di campi non vincenti e dividerli di nuovo per il numero totale di campi. Per esempio, la probabilità di perdere se si scommette sul rosso è 19/37 (18 campi neri + zero verde).
📌 Nota: Per ridurre una frazione a 1/x, basta dividere il numeratore e il denominatore per il numeratore. Per esempio, 18/37 (si dividono entrambi i numeri per 18) sarà 1/2,055 dopo la regolazione. E quindi questo significa che per ogni 2,055 giri, un giro risulterà in un rosso o in un nero.
Probabilità di rotazioni multiple
Una volta che hai imparato il calcolo per i giri singoli, calcolare la probabilità per i giri multipli è molto semplice. Basta moltiplicare le singole frazioni l'una per l'altra.
Esempi:
- spin - puntata sul rosso = 18/37
- spin - puntata per dozzina = 12/37
Probabilità di vincere entrambi i round = (18/37)*(12/37)=1/6.34 o 15.77% o 5.34 a 1
- spin - straight bet - 1/37
- spin - straight bet - 1/37
Probabilità di vincere entrambi i round = (1/37)*(1*37)=1/1369 o 0,073% o 1368 a 1
- spin - scommettere sul nero e dispari 9/37
- spin - scommettere sul pari 18/37
- spin - colonna scommessa 12/37
Probabilità di vincere tutti e 3 i round = (9/37)*(18/37)*(12/37)=1/26.06 o 3.84% o 25.06 a 1
La conversione effettiva tra le voci è di nuovo molto facile. Si ottengono le percentuali dividendo la frazione nella forma 1/x e poi moltiplicando per 100. Si ottiene la notazione proporzionale sotto forma di X a 1 sottraendo 1 dal denominatore, che è il giro vincente del totale. Vedi gli esempi sopra il paragrafo.
Probabilità dei dadi
I dadi sono un altro gioco d'azzardo in cui è relativamente facile calcolare le probabilità. Prima di entrare nel calcolo delle probabilità di vincita ai dadi, diamo un'occhiata alle probabilità di lancio dei dadi stessi.
I dadi hanno 6 lati. La probabilità che un qualsiasi numero cada è quindi 1/6. Il craps è tradizionalmente giocato con due dadi. Le probabilità che due numeri qualsiasi si combinino sono quindi 2/36. Tuttavia, non siamo tanto interessati ai numeri specifici quanto alla somma di quei numeri, che è molto più importante nei dadi. Di nuovo, useremo la formula: numero di combinazioni vincenti/numero di tutte le combinazioni.
Diciamo che vogliamo conoscere la probabilità per la somma di 7. Combinazioni vincenti: (1-6), (2-4), (3-3), (4-2), (6-1). Come puoi vedere, ci sono un totale di 6 diverse combinazioni in cui la somma di 7 può essere lanciata su due dadi. E poiché il numero di tutte le combinazioni è 36, la probabilità di 7 è 6/36=0,1666
In questo modo, tutti gli altri possibili risultati possono essere facilmente calcolati.
|
Totale |
Probabilità |
|
2 |
1/36 |
|
3 |
2/36 |
|
4 |
3/36 |
|
5 |
4/36 |
|
6 |
5/36 |
|
7 |
6/36 |
|
8 |
5/36 |
|
9 |
4/36 |
|
10 |
3/36 |
|
11 |
2/36 |
|
12 |
1/36 |
Probabilità di vincere ai dadi
Brevemente, diamo un'occhiata alle regole dei dadi. La scommessa più comune è la Pass Line.
- Se esce un 7 o un 11, si vince
- Se si tira un 2, 3 o 12, si perde
- Negli altri casi (4, 5, 6, 8, 9 o 10) si determina un punto e si tira finché non si tira di nuovo quel punto (vincere) o si tira un 7 (perdere)
Calcoliamo prima la probabilità di vincere prima di determinare il punto. La possibilità di colpire 7 è 6/36 e la possibilità di colpire 11 è 2/36. Queste due frazioni devono poi essere sommate per dare 3/36+2/36 = 2/9 = 0,2222.
Ora rivolgiamo la nostra attenzione alla situazione in cui un punto è determinato. Cioè quando il punto è 4, 5, 6, 8, 9 o 10. Cominciamo con un totale di 4.
Se esce un 4, si determina un punto e il giocatore tira finché non esce un 4 o un 7. È qui che entriamo nel regno della probabilità condizionata. Questo ci dice qual è la probabilità dell'evento A se l'evento B si verifica nello stesso momento. Nel nostro caso, sarà la probabilità di vincere (tira un 4) se il round finisce (tira un 4 o un 7). Poi inseriamo questi valori nella formula:
- P(A) = caduta somma di 4: 3/36
- P(A∩B) = dopo aggiustamenti troviamo che è uguale a A
- P(B) = caduta 4 o 7: 3/36 + 6/36 = 9/36
Ne consegue che:
- P(4|4 o 7) = (3/36)/(9/36) = 1/3
In modo simile possiamo calcolare le somme di 5, 6, 8, 9 e 10
- P(5|5 o 7) = (4/36)/(10/36) = 2/5
- P(6|6 o 7) = (5/36)/(11/36) = 5/11
- P(8|8 o 7) = (5/36)/(11/36) = 5/11
- P(9|9 o 7) = (4/36)/(10/36) = 2/5
- P(10|10 o 7) = (3/36)/(9/36) = 1/3
Ora possiamo calcolare la probabilità di vincere come la probabilità del lancio originale quando il punto è stato determinato e il lancio successivo quando il giocatore ha vinto.
- Rotolo originale 4 x P(4|4 o 7) = 3/36 x 1/3 = 1/36
- Lancio originale 5 x P(5|5 o 7) = 4/36 x 2/5 = 2/45
- Rotolo originale 6 x P(6|6 o 7) = 5/36 x 5/11 = 25/396
- Rotolo originale 8 x P(8|8 o 7) = 5/36 x 5/11 = 25/396
- Lancio originale 9 x P(9|9 o 7) = 4/36 x 2/5 = 2/45
- Rotolo originale 10 x P(10|10 o 7) = 3/36 x 1/3 = 1/36
Tutte queste frazioni ci danno la probabilità di vincere se il primo lancio è 4, 5, 6, 8, 9 o 10. Se vuoi conoscere la probabilità totale di vincere su una scommessa Pass line, devi sommarle tutte e aggiungere la probabilità di vincere prima del punto (tira un 7 o un 11 - 2/9).
2/9 + 1/36 + 2/45 + 25/396 + 25/396 + 2/45 + 1/36 = 244/495
Perché 244/495 è esattamente il 49,3%. È poco meno del 50%. Infatti, probabilmente non troverai una migliore possibilità di vincere con un payout di 1 su 1. Tranne forse il blackjack, se sai contare le carte.
Probabilità di Blackjack
Il blackjack è il gioco d'azzardo in cui le probabilità contano di più. Nel blackjack, puoi influenzare il margine della casa con la tua abilità e conoscenza. Hai solo bisogno di conoscere la strategia ottimale per questo, e se sai come contare le carte, potrai anche giocare con il vantaggio del giocatore. Non è necessario conoscere tutte le probabilità specifiche, perché tutti questi calcoli sono già stati fatti dai matematici prima di te che hanno inventato tutte le tattiche e le strategie del blackjack.
Tuttavia, per motivi di interesse, mostreremo come calcolare la probabilità per alcuni fenomeni importanti nel blackjack.
Se guardiamo il problema della probabilità dalla prospettiva di un mazzo di carte, è chiaro che il numero di risultati possibili aumenta rapidamente. Il blackjack si gioca con un mazzo di 52 carte, 4 semi e 13 valori. Questo dà le seguenti probabilità:
- Prendo un Asso dal mazzo (o qualsiasi carta individuale): 4/52=0,0769 (7,69%)
- Prendo una picche dal mazzo: 13/52=0,25 (25%)
Tuttavia, a differenza del lancio di una moneta, della roulette o delle slot machine per esempio, un mazzo di carte ha una sorta di "memoria". O meglio, significa che i risultati precedenti hanno un effetto sulle mosse attuali e future. Questo è dovuto al fatto che una carta è stata tolta dal mazzo e questo cambia la situazione di partenza. Guardiamo un esempio in cui la prima carta estratta da un mazzo di 52 carte è un Asso (7,69% di probabilità). La probabilità che un Asso venga estratto di nuovo come seconda carta dal mazzo sarà ora diversa. Dopo la prima estrazione, il numero di assi è sceso a 3 e il numero di carte a 51.
Probabilità per il blackjack naturale
Ciò a cui ogni giocatore sarà interessato per prima cosa è la probabilità del blackjack. Cioè, quali sono le probabilità che un giocatore ottenga un asso e una carta da dieci proprio all'inizio del turno - in altre parole, un naturale.
Questa situazione può verificarsi in due modi, e se sommiamo i due modi, otteniamo le nostre probabilità sul blackjack:
📌 Nota: stiamo contando per il blackjack a mazzo singolo. Quindi 52 carte, 4 assi e 16 dieci. La carta del mazziere non è visibile, quindi non influenzerà la probabilità.
- Il giocatore ottiene il primo asso e una carta da dieci
Al giocatore viene distribuita la prima carta Asso con una probabilità di 4/52. Quindi il giocatore deve ottenere la seconda carta con un dieci, e per questo le probabilità sono 16/51. Queste due probabilità devono essere moltiplicate tra loro per ottenere 16/663.
- Il giocatore riceve la prima carta da dieci e un asso
La probabilità che un giocatore riceva la prima carta con un valore di 10 è 16/52. Le probabilità che un giocatore ottenga un Asso dopo questo sono 4/51. Dopo aver moltiplicato, otteniamo 16/663.
Se vogliamo conoscere la probabilità di ottenere un blackjack aggiungiamo semplicemente questi due fenomeni. Quindi 16/663 + 16/663 = 32/663 = 4,827%. In altre parole, un giocatore ottiene un blackjack circa una volta ogni 20 mani. Puoi calcolare la probabilità per i tavoli multi-deck in un modo simile, che abbiamo già fatto per te.
|
Numero di pacchetti |
Probabilità |
|
1 |
4,827 % |
|
2 |
4,780 % |
|
3 |
4,764 % |
|
4 |
4,757 % |
|
5 |
4,752 % |
|
6 |
4,749 % |
Probabilità per il busto
Potrebbe anche essere interessante sapere quali sono le vostre probabilità di un fallimento. Di nuovo, ci concentreremo su una situazione di esempio in cui stai giocando solo con il mazziere ad un tavolo con un solo mazzo. Diamo un'occhiata a una situazione molto semplice in cui un giocatore ha 2 carte con un valore di 10 in totale, quindi ha 20 punti. In una situazione in cui il giocatore ottiene una terza carta, sono già state giocate 3 carte dal mazzo. Questo lascia 49 carte nel mazzo. Di queste 49 carte, solo 4 assi vi aiuteranno. Di queste 49, 45 carte sono indesiderate. Pertanto, le probabilità di un arresto sono 45/49=0,9183673.
Si possono calcolare altre probabilità in modo simile. Bisogna sempre essere in grado di immaginare correttamente la situazione. Questo è tutto.
|
Valore della mano |
Probabilità di arresti |
|
21 |
100 % |
|
20 |
92 % |
|
19 |
85 % |
|
18 |
77 % |
|
17 |
69 % |
|
16 |
62 % |
|
15 |
58 % |
|
14 |
56 % |
|
13 |
39 % |
|
12 |
31 % |
|
11 meno |
0 % |
Diamo poi un'occhiata a quanto è probabile che il mazziere si rompa per ogni carta.
|
Valore della mano |
Probabilità di arresti |
|
2 |
35,30 % |
|
3 |
37,56 % |
|
4 |
40,28 % |
|
5 |
42,89 % |
|
6 |
42,08 % |
|
7 |
25,99 % |
|
8 |
23,86 % |
|
9 |
23,34 % |
|
10, J, Q, K |
21,43 % |
|
Asso |
11,65 % |
Probabilità di poker
Il poker è un altro gioco di carte in cui la probabilità è estremamente importante. Tra le altre cose. Quindi diamo un'occhiata a quali sono le tue possibilità a poker.
Probabilità pre-flop
Ora che abbiamo delineato come funziona la probabilità in un mazzo di carte, passiamo alle applicazioni pratiche. Prima di tutto, mostreremo come calcolare la probabilità di esaurire le coppie in una mano. (per esempio, il tanto discusso Aces). In questo caso, dobbiamo moltiplicare le probabilità l'una per l'altra.
(4/52) x (3/51) = (12/2652) = (1/221) = 0,004524 (0,45 %)
📌 Nota: se giochi a poker in un casinò che distribuisce circa 30 mani all'ora, otterrai una coppia d'assi circa una volta ogni 7 ore e mezza di gioco.
Quindi quali sono le possibilità di ottenere una delle 13 possibili coppie quando dai le carte? Possiamo assumere che le probabilità siano 1/221 per coppia individuale (vedi formula sopra). Ci possono essere 13 di queste coppie in totale, quindi la formula per il calcolo sarà 13/221=0,0588. Quindi ci si può aspettare una coppia circa una volta ogni 35 partite.
Probabilità nel poker giocatore contro giocatore
Tuttavia, il poker è un gioco multiplayer, di solito giocato l'uno contro l'altro. Ecco quindi una selezione delle più comuni situazioni pre-flop.
|
La tua mano |
Mano del tuo avversario |
Probabilità di vincita |
|
Coppia alta |
Due carte basse |
83 % |
|
Coppia alta |
Coppia bassa |
82 % |
|
Coppia centrale |
Carta alta, carta bassa |
71 % |
|
Due carte alte |
Due carte basse |
63 % |
|
Due carte alte |
Coppia bassa |
55 % |
Calcolo della probabilità per "outs"
Se riesci a vedere le carte sul flop, sarai certamente più interessato a sapere quali sono le tue possibilità di migliorare la tua mano. In questo caso, parleremo dei cosiddetti "out". Nel poker, questo termine si riferisce a qualsiasi carta che può aiutarti. Un caso così comune può essere quando un giocatore possiede due carte di un seme e altre due carte dello stesso seme appaiono sul flop. Il giocatore ha quindi 4 carte per fare colore e quindi ha 9 out, lasciando 9 carte con cui formare un colore.
|
Numero di uscite |
Flop - Turn |
Turn - River |
Girare un fiume |
|
20 |
42,6 % |
43,5 % |
67,5 % |
|
19 |
40,4 % |
41,3 % |
65,0 % |
|
18 |
38,3 % |
39,1 % |
62,4 % |
|
17 |
36,2 % |
37,0 % |
59,8 % |
|
16 |
34,0 % |
34,8 % |
57,0 % |
|
15 |
31,9 % |
32,6 % |
54,1 % |
|
14 |
29,8 % |
30,4 % |
51,2 % |
|
13 |
27,7 % |
28,3 % |
48,1 % |
|
12 |
25,5 % |
26,1 % |
45,0 % |
|
11 |
23,4 % |
23,9 % |
41,7 % |
|
10 |
21,3 % |
21,7 % |
38,4 % |
|
9 |
19,1 % |
19,6 % |
35,0 % |
|
8 |
17,0 % |
17,4 % |
31,5 % |
|
7 |
14,9 % |
15,2 % |
27,8 % |
|
6 |
12,8 % |
13,0 % |
24,1 % |
|
5 |
10,6 % |
10,9 % |
20,3 % |
|
4 |
8,5 % |
8,7 % |
16,5 % |
|
3 |
6,4 % |
6,5 % |
12,5 % |
|
2 |
4,3 % |
4,3 % |
8,4 % |
|
1 |
2,1 % |
2,2 % |
4,3 % |
📌 Nota: C'è un metodo molto facile per calcolare la probabilità di out, quindi puoi farlo direttamente al tavolo. È generalmente chiamata la regola del "quattro e due". Dopo il flop, il giocatore moltiplica semplicemente il numero di out per 4 per trovare la probabilità di turn e river. Se non ottiene la carta sul turn, moltiplica semplicemente il numero di out per due per ottenere la probabilità approssimativa di ottenere la carta sul river.
Di nuovo, possiamo usare l'esempio di avere 4 carte dello stesso seme dopo il flop. Quindi i tuoi out sono 9 carte e la probabilità di un colore dopo il turn e il river è del 36% (9x4). Diciamo che non si ottiene una carta nel turno. In questo caso, moltiplichiamo gli out per due e troviamo che abbiamo il 18% (9x2) di possibilità di esaurire le carte del seme sul river. Come potete vedere confrontando la tabella, questo metodo è davvero semplice ma d'altra parte impreciso, ma può essere usato.

 IT
IT  English
English  čeština
čeština  Polski
Polski  Slovenčina
Slovenčina  Русский
Русский  Deutsch
Deutsch  Slovenski
Slovenski  Dutch
Dutch  Svenska
Svenska  Português
Português  Español
Español  Français
Français  Suomalainen
Suomalainen  Български
Български  Românesc
Românesc  Magyar
Magyar  Eesti
Eesti  Ελληνική
Ελληνική  Latviešu
Latviešu  Lietuvių
Lietuvių  やまと
やまと  中国
中国  Dansk
Dansk  Türkçe
Türkçe  ID
ID  Українська
Українська  한국어
한국어  Norsk
Norsk 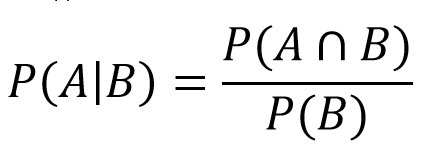


Devi essere logato per aggiungere un commento