Valószínűség és kaszinójátékok
 Peter Sommer
Peter Sommer
Tisztában vagy az esélyeiddel? Ha egy kaszinóban fog játszani, győződjön meg róla, hogy ismeri és tökéletesen megérti az esélyeit. Miért? Mert a valószínűség a kaszinók motorja. Valószínűség nélkül a szerencsejáték-ipar nem lenne lehetséges.
A véletlen egyszerűen annak a valószínűsége, hogy valami megtörténik. A valószínűség a mindennapi életünk része. Amikor úgy döntünk, hogy piros lámpánál átmegyünk egy forgalmas utcán, van rá némi esély, hogy elüt egy autó, de cserébe esélyünk van arra, hogy gyorsabban átkelünk az úton, és nyerünk egy kis időt.
Amikor szerencsejátékot játszunk, megbecsüljük egy bizonyos esemény bekövetkezésének valószínűségét, hogy megfogalmazzuk a tétünket. Ezekben az esetekben számoljuk ki a valószínűséget.
💡 Valószínűségi példa
Tegyük fel, hogy van egy zsákunk, amelyben négy golyó van, amelyek közül csak egy piros, a másik három pedig kék. Annak a valószínűsége, hogy csak a piros golyót húzzuk ki anélkül, hogy megnéznénk, 1:4.
A valószínűséget többféleképpen is ki lehet fejezni. Azt is mondhatjuk, hogy a piros ellen 3:1 az esély, mert átlagosan három kék golyót húzunk minden egyes húzott piros golyóra.
Az esélyeinket százalékban is kifejezhetjük, így a piros golyó kihúzásának valószínűsége 25%, ha a golyó kihúzásának esélye 100%. Tehát 100 osztva néggyel 25%-ot kapunk.
A kék golyó kihúzásának valószínűsége 75%, ha három kék golyó van, amelyek kihúzásának esélye 25%.
A kaszinójátékok valószínűsége
A kaszinó azon az elven működik, hogy a hosszú távú eredményeinket tekintve nem túl jó oddsokat kínál.
A léggömbökkel teli zsák példájával egyszerűen bemutatható, hogyan működik egy kaszinó. Tegyük fel, hogy egy kaszinó 3 esélyt kínál egy piros golyó kihúzására. Ha 5 $-t teszel fel, akkor négy próbálkozás során átlagosan háromszor húzod meg a kék golyót, és 15 $-t veszítesz, a negyedik alkalommal pedig a piros golyót húzod meg, és 10 $-t nyersz, de a kaszinó még mindig 5 $-t veszít.
Minden szerencsejáték csak a valószínűségről szól. Ezt minden tapasztalt szerencsejátékos meg fogja mondani. Ezért elengedhetetlen, hogy ismerjük ezeket a számokat, és tudjuk, hogyan kell velük dolgozni. Ezért most megmutatjuk, hogyan kell kiszámítani a szerencsejátékok valószínűségét. Ha jól érti az elvet, akkor bármi másnak a valószínűségét is kiszámíthatja vele.
Valószínűség a rulettben
A rulett olyan, mint a szerencsekerék. És tudod miért? Mindössze 3 szóra van szükség a magyarázathoz - Nagyszám-elmélet. Minden olyan személy, aki kaszinót üzemeltet vagy online kaszinójátékokat gyárt, nagyon jól ismeri ezt az elméletet. Mert ez közvetlenül kapcsolódik a keresetéhez. És ennek köszönhetően a kaszinó hosszú távon is mindig nyer a fogadókkal szemben. Minden a valószínűséghez és a ház előnyéhez kapcsolódik.
📌 Megjegyzés: A cikkben szereplő összes szám az európai rulettre vonatkozik - tehát 37 számot számolunk.
Hogyan kell valószínűséget írni
A valószínűséget többféleképpen lehet leírni. A legismertebb talán a százalékos arányok. Ezek mellett törtet vagy arányt használó kifejezéseket is használnak.
- Százalékban kifejezve (%) - itt nincs sok hozzáfűznivaló, de csak a teljesség kedvéért, ez a kiválasztott esemény százalékos aránya. A számítása a következő: (rész/összesség)*100. Például a kiválasztott szám eltalálásának valószínűsége a rulettkeréken (egyenes): 1/37*100=2,7%.
- Kifejezés törtekkel (1/x) - Amikor a valószínűséget törtekkel fejezzük ki, azt mondjuk, hogy a jelenség X próbálkozásból 1 alkalommal fordul elő. Egy numerikus kifejezésben a százalékok kiszámítására támaszkodunk. Ha a fenti 1/37-es példát vesszük alapul, ez azt jelenti, hogy egy statisztikailag kiválasztott szám a rulettkeréken 37 pörgetésből 1 alkalommal fog esni.
- Kifejezés arányosan (x-1) - Minden alkalommal, amikor X bekövetkezik, a kiválasztott jelenség 1-szer történik meg. Itt is maradunk a kiválasztott szám valószínűségénél a rulettnél. Ebben az esetben az arány 36:1. Ez azt jelenti, hogy minden 36 olyan pörgetés után, amikor a szám nem esik, lesz egy olyan pörgetés, amikor a kiválasztott szám esik.
📌 Megjegyzés: Ahogy a nagy számelmélet mondja, a valószínűség lényegében egy matematikai határérték. Egyre több próbálkozással reálisan egyre közelebb kerül a számított eredményhez.
Amint láthatod, a törteket és az arányokat használó kifejezések nagyon hasonlóak. Az egyetlen különbség az, hogy a töredék az összes pörgetést számolja, míg az arány az összes pörgetést két kategóriára osztja.
Az egyes fogadások valószínűségének táblázata a rulettben
|
Fogadás |
Részlet a |
Ratio |
Százalékok |
|
Egyenes tét |
1/2,055 |
1,055-1 |
48,6 % |
|
Oszlop |
1/3,08 |
2,08:1 |
32,4 % |
|
A tucat |
1/3,08 |
2,08:1 |
32,4 % |
|
Hat vonal |
1/6,17 |
5,17-1 |
16,2 % |
|
Sarok |
1/9,25 |
8,25:1 |
10,8 % |
|
Street |
1/12,33 |
11,33:1 |
8,1 % |
|
Split |
1/19,5 |
18,5:1 |
5,4 % |
|
Egyenes |
1/37 |
36:1 |
2,7 % |
Egyenes fogadás valószínűsége
A kiválasztott jelenség ismétlődésének matematikai összehasonlítása is érdekes lehet. Ebben az esetben egy egyenes fogadást választottunk, konkrétan például egy pirosra tett tétet. Szóval, mi lesz a változó valószínűsége annak, hogy például 5 alkalommal egymás után piros lesz?
|
Pörgetések száma |
Ratio |
Százalékok |
|
1 |
1,06-1 |
48,6 % |
|
2 |
3,23:1 |
23,7 % |
|
3 |
7,69:1 |
11,5 % |
|
4 |
16,9:1 |
5,6 % |
|
5 |
35,7:1 |
2,73 % |
|
6 |
74,4:1 |
1,33 % |
|
7 |
154-1 |
0,65 % |
|
8 |
318-1 |
0,31 % |
|
9 |
654-1 |
0,15 % |
|
10 |
1 346-1 1 |
0,074 % |
|
15 |
49 423-1 |
0,002 % |
|
20 |
1 813 778-1 |
0,000055 % |
Mint látható, a pörgések számának növekedésével a jelenség valószínűsége gyorsan csökken. Ne feledje azonban, hogy ezek a valószínűségek a jelenség egészét írják le. A véletlenszám-generátor nem veszi figyelembe a korábbi eredményeket, így annak ellenére, hogy 1,813 millió játékban egyszer fordul elő olyan játéksorozat, amelyben a piros 20-szor egymás után eltalál, a 21 játékkör ugyanolyan házelőnnyel és valószínűséggel (azaz 48,6%-kal) jár, mint minden más játékkör.
Ebben az esetben gyakran találkozhatunk a Player's Fallacy kifejezéssel, amikor a fogadó azt hiszi, hogy ha egy színt többször eltalál egymás után, akkor nagyobb a valószínűsége annak, hogy a következő pörgetésnél a másik színt is eltalálja. A valóságban ez nem így van. Ennek a tévedésnek a leghíresebb esetét 1913-ban figyelték meg a Monte Carlo-i kaszinóban, amikor a rulettkeréken egymás után 26-szor esett a fekete szín, és az emberek e hihetetlen sorozat szinte teljes időtartama alatt, és még a vége után is frenetikusan a pirosra fogadtak. Ekkor a kaszinó nagyon szép pénzt keresett.
📌 Megjegyzés: Annak valószínűsége, hogy egy színt 26-szor egymás után eltalálnak, 0,000000730870%, és 67 millió játékból egyszer fordul elő.
Hogyan kell kiszámítani a rulett valószínűségét?
Szeretne több esélyt megtudni az egyes fogadásokhoz? Próbálja meg maga kiszámítani őket. A százalékokkal és valószínűségekkel való munka nem túl bonyolult. Általában az a legegyszerűbb, ha a törtekkel kezdjük, és ezekből számoljuk ki a további százalékokat és arányokat. Ha például ki akarod számítani a valószínűséget egy törtben egy olyan helyzetre, amikor a piros a piros, akkor a következőket kell tenned:
A pirosak száma a játéktéren / a játékterek száma összesen = 18/37
Egy pörgetés valószínűsége
Itt is egy egyszerű szabály érvényes. Egyszerűen számítsa ki, hogy hány mezővel nyerhet, és ossza el a mezők teljes számával.
Például:
- Szín - 18/37
- Még/Páratlan - 18/37
- Tucatnyi - 12/37
- Szám 0 - 1/37
- Fekete és páros - 9/37 (csak 9 olyan szám van a játékmezőben, amely fekete és páros)
- Tízes és oszlop - 4/37 (egy tucatban és egy oszlopban csak 4 szám van)
A nyerés valószínűségéhez hasonlóan kiszámíthatod a vesztés valószínűségét is. Csak számolja meg a nem nyertes mezők számát, és ossza el őket ismét a mezők teljes számával. Például a pirosra tett tét esetén a veszteség valószínűsége 19/37 (18 fekete mező + zöld nulla).
📌 Megjegyzés: Ha egy törtet 1/x-re akarsz csökkenteni, egyszerűen oszd el a számlálót és a nevezőt a számlálóval. Például a 18/37 (mindkét számot elosztja 18-cal) a kiigazítás után 1/2,055 lesz. Ez azt jelenti, hogy minden 2,055 fordulóból egy forduló piros vagy fekete lesz.
Többszörös pörgés valószínűsége
Ha már elsajátította az egyszeri pörgetések számítását, a többszörös pörgetések valószínűségének kiszámítása nagyon egyszerű. Csak szorozza meg az egyes törteket egymással.
Példák:
- pörgetés - tét a pirosra = 18/37
- pörgetés - tét tucatonként = 12/37
Mindkét forduló megnyerésének valószínűsége = (18/37)*(12/37)=1/6,34 vagy 15,77% vagy 5,34:1.
- pörgetés - egyenes tét - 1/37
- pörgetés - egyenes tét - 1/37
Mindkét forduló megnyerésének valószínűsége = (1/37)*(1*37)=1/1369 vagy 0,073% vagy 1368:1.
- spin - tét fekete és páratlan 9/37
- pörgetés - páros tét 18/37
- spin - oszlop tét 12/37
Mindhárom forduló megnyerésének valószínűsége = (9/37)*(18/37)*(12/37)=1/26,06 vagy 3,84% vagy 25,06:1.
A bejegyzések közötti tényleges átalakítás ismét nagyon egyszerű. A százalékokat úgy kapjuk meg, hogy a törtet 1/x alakban osztjuk, majd megszorozzuk 100-zal. Az X-1 arányos jelölést úgy kapjuk meg, hogy a nevezőből kivonjuk az 1-et, ami az összeg nyertes körét jelenti. Lásd a bekezdés feletti példákat.
A kocka valószínűsége
A kockázás egy másik olyan szerencsejáték, amelyben viszonylag könnyű kiszámítani az esélyeket. Mielőtt belemennénk a kockadobás nyerési esélyeinek kiszámításába, vessünk egy pillantást magára a kockadobás valószínűségére.
A kockának 6 oldala van. Annak az esélye, hogy bármelyik szám leesik, 1/6. A craps-et hagyományosan két kockával játsszák. A két szám kombinációjának esélye tehát 2/36. Minket azonban nem annyira a konkrét számok érdekelnek, mint inkább a számok összege, ami sokkal fontosabb a kockajátékban. Ismét a következő képletet használjuk: nyerő kombinációk száma/az összes kombináció száma.
Tegyük fel, hogy a 7-es összeg valószínűségére vagyunk kíváncsiak. Nyerő kombinációk: (1-6), (2-4), (3-3), (4-2), (6-1). Amint láthatod, összesen 6 különböző kombináció létezik, ahol a 7-es összeg két kockával dobható. És mivel az összes kombináció száma 36, a 7 valószínűsége 6/36=0,1666.
Így minden más lehetséges eredmény könnyen kiszámítható.
|
Összesen |
Valószínűség |
|
2 |
1/36 |
|
3 |
2/36 |
|
4 |
3/36 |
|
5 |
4/36 |
|
6 |
5/36 |
|
7 |
6/36 |
|
8 |
5/36 |
|
9 |
4/36 |
|
10 |
3/36 |
|
11 |
2/36 |
|
12 |
1/36 |
A nyerési esélyek a crapsben
Röviden nézzük meg a kocka szabályait. A leggyakoribb fogadás a Pass Line.
- Ha 7-et vagy 11-et dobsz, nyersz.
- Ha 2-est, 3-ast vagy 12-est dobsz, veszítesz.
- Más esetekben (4, 5, 6, 8, 9 vagy 10) egy pontot határoznak meg, és addig dobnak, amíg az adott pontot újra nem dobják (győzelem) vagy 7-et dobnak (vesztés).
A pont meghatározása előtt először kiszámítjuk a győzelem valószínűségét. A 7-es találat esélye 6/36, a 11-es találat esélye pedig 2/36. Ezt a két törtet össze kell adni, így kapjuk a 3/36+2/36 = 2/9 = 0,2222 értéket.
Most fordítsuk figyelmünket arra a helyzetre, amikor egy pontot határozunk meg. Vagyis amikor a pont 4, 5, 6, 8, 9 vagy 10. Kezdjük összesen 4-gyel.
Ha 4-es dobás történik, akkor egy pont kerül meghatározásra, és a játékos addig dob, amíg 4-es vagy 7-es dobás nem történik. Itt lépünk be a feltételes valószínűség birodalmába. Ez megmondja, hogy mekkora az A esemény valószínűsége, ha a B esemény ugyanabban az időben következik be. A mi esetünkben ez az lesz, hogy mi a valószínűsége annak, hogy nyerünk (4-es dobás), ha a kör véget ér (4-es vagy 7-es dobás). Ezután ezeket az értékeket beillesztjük a képletbe:
- P(A) = Falls 4 összege: 3/36
- P(A∩B) = a kiigazítások után azt találjuk, hogy egyenlő A-val
- P(B) = 4-es vagy 7-es esés: 3/36 + 6/36 = 9/36
Ebből következik:
- P(4|4 vagy 7) = (3/36)/(9/36) = 1/3
Hasonló módon kiszámíthatjuk az 5, 6, 8, 9 és 10 összegét is.
- P(5|5 vagy 7) = (4/36)/(10/36) = 2/5
- P(6|6 vagy 7) = (5/36)/(11/36) = 5/11
- P(8|8 vagy 7) = (5/36)/(11/36) = 5/11
- P(9|9 vagy 7) = (4/36)/(10/36) = 2/5
- P(10|10 vagy 7) = (3/36)/(9/36) = 1/3
Most már kiszámíthatjuk a nyerési esélyt, mint az eredeti dobás valószínűségét, amikor a pont meghatározásra került, és a következő dobásét, amikor a játékos nyert.
- Eredeti dobás 4 x P(4|4 vagy 7) = 3/36 x 1/3 = 1/36
- Eredeti dobás 5 x P(5|5 vagy 7) = 4/36 x 2/5 = 2/45
- Eredeti dobás 6 x P(6|6 vagy 7) = 5/36 x 5/11 = 25/396
- Eredeti dobás 8 x P(8|8 vagy 7) = 5/36 x 5/11 = 25/396
- Eredeti dobás 9 x P(9|9 vagy 7) = 4/36 x 2/5 = 2/45
- Eredeti dobás 10 x P(10|10 vagy 7) = 3/36 x 1/3 = 1/36
Mindezek a törtek megadják a nyerés valószínűségét, ha az első dobás 4, 5, 6, 8, 9 vagy 10-es. Ha tudni szeretné a Pass line tét teljes nyerési valószínűségét, akkor össze kell adnia az összeset, és hozzá kell adnia a pont előtti nyerési esélyt (7-es vagy 11-es dobás - 2/9).
2/9 + 1/36 + 2/45 + 25/396 + 25/396 + 2/45 + 1/36 = 244/495
Mert 244/495 pontosan 49,3%. Ez valamivel kevesebb, mint 50%. Valójában valószínűleg nem fogsz találni jobb nyerési esélyt az 1:1 kifizetésnél. Kivéve talán a blackjacket, ha tudod számolni a kártyákat.
Blackjack valószínűsége
A blackjack a szerencsejáték, amelyben az esélyek számítanak a legtöbbet. A blackjackben ügyességeddel és tudásoddal befolyásolhatod a ház előnyét. Ehhez csak ismerned kell az optimális stratégiát, és ha tudod, hogyan kell számolni a lapokat, akkor még a játékosok előnyével is játszhatsz. Körülbelül nem is kell ismerned az összes konkrét valószínűséget, mert ezeket a számításokat már előtted is elvégezték a matematikusok, akik kitalálták a blackjack összes taktikáját és stratégiáját.
Az érdekesség kedvéért azonban megmutatjuk, hogyan lehet kiszámítani a blackjack néhány fontos jelenségének valószínűségét.
Ha a valószínűségi problémát egy kártyapakli szemszögéből nézzük, akkor egyértelmű, hogy a lehetséges kimenetek száma gyorsan növekszik. A blackjacket 52 lapból álló paklival, 4 színnel és 13 értékkel játsszák. Ez a következő esélyeket adja:
- Ászt húzok a pakliból (vagy bármilyen egyedi lapot): 4/52=0.0769 (7.69%)
- Pikket húzok a pakliból: 13/52=0.25 (25%)
Azonban, ellentétben például az érmefeldobással, a rulettel vagy a nyerőgépekkel, a kártyapakli rendelkezik valamiféle "memóriával". Vagy inkább azt jelenti, hogy a korábbi eredmények hatással vannak a jelenlegi és a jövőbeli lépésekre. Ez annak köszönhető, hogy egy lap kiesett a pakliból, és ez megváltoztatja a kiindulási helyzetet. Nézzünk egy példát, ahol az 52 lapos pakliból elsőként egy ászt húztak (7,69% esély). Annak a valószínűsége, hogy a pakli második lapjaként ismét egy ász kerül kihúzásra, most más lesz. Az első húzás után az ászok száma 3-ra, a lapok száma pedig 51-re csökkent.
Valószínűség blackjack természetes
Ami minden játékost először érdekel, az a blackjack valószínűsége. Vagyis mekkora az esélye annak, hogy egy játékos a kör elején egy ász és egy tízes lapot kap - más szóval, egy természetes lapot.
Ez a helyzet kétféleképpen fordulhat elő, és ha a két lehetőséget összeadjuk, megkapjuk a blackjack esélyeit:
📌 Megjegyzés: Egy pakli blackjack esetén számolunk. Tehát 52 lap, 4 ász és 16 tízes. Az osztó lapja nem látható, így az nem befolyásolja a valószínűséget.
- A játékos megkapja az első ászt és egy tízes kártyát.
A játékos 4/52 valószínűséggel kapja az első ász kártyát. A játékosnak tehát a második lapot tízessel kell megkapnia, és erre 16/51 az esély. Ezt a két valószínűséget meg kell szorozni egymással, hogy megkapjuk a 16/663-at.
- A játékos megkapja az első tízes kártyát és egy ászt.
Annak a valószínűsége, hogy egy játékos az első 10-es értékű lapot kapja, 16/52. Annak az esélye, hogy a játékos ezután ászra talál, 4/51. A szorzás után 16/663-at kapunk.
Ha tudni akarjuk, hogy mekkora a valószínűsége annak, hogy blackjack-et kapunk, akkor csak össze kell adnunk ezt a két jelenséget. Tehát 16/663 + 16/663 = 32/663 = 4,827%. Más szóval, egy játékos körülbelül minden 20. leosztásban kap blackjacket. A több pakliból álló asztalok valószínűségét hasonló módon számolhatja ki, amit mi már megtettünk Önnek.
|
Csomagok száma |
Valószínűség |
|
1 |
4,827 % |
|
2 |
4,780 % |
|
3 |
4,764 % |
|
4 |
4,757 % |
|
5 |
4,752 % |
|
6 |
4,749 % |
A buktatás valószínűsége
Az is érdekes lehet, hogy mi az esélye a bukásnak. Ismét egy olyan mintaszituációra összpontosítunk, amikor csak az osztóval játszol egy egylapos asztalnál. Nézzünk meg egy nagyon egyszerű helyzetet, amikor egy játékosnak 2 kártyája van, amelyek értéke összesen 10, így 20 pontja van. Abban a helyzetben, amikor a játékos egy harmadik kártyát kap, már 3 kártyát játszott ki a pakliból. Így 49 lap marad a pakliban. Ebből a 49 lapból csak 4 ász fog segíteni. Ebből a 49-ből 45 kártya nemkívánatos. Ezért a lebukás esélye 45/49=0,9183673.
Hasonló módon más valószínűségeket is kiszámíthat. Mindig helyesen kell tudni elképzelni a helyzetet. Ez minden.
|
A kéz értéke |
A csődök valószínűsége |
|
21 |
100 % |
|
20 |
92 % |
|
19 |
85 % |
|
18 |
77 % |
|
17 |
69 % |
|
16 |
62 % |
|
15 |
58 % |
|
14 |
56 % |
|
13 |
39 % |
|
12 |
31 % |
|
11 kevesebb |
0 % |
Nézzük meg, hogy az osztó milyen valószínűséggel fog buktatni az egyes lapoknál.
|
A kéz értéke |
A csődök valószínűsége |
|
2 |
35,30 % |
|
3 |
37,56 % |
|
4 |
40,28 % |
|
5 |
42,89 % |
|
6 |
42,08 % |
|
7 |
25,99 % |
|
8 |
23,86 % |
|
9 |
23,34 % |
|
10, J, Q, K |
21,43 % |
|
Ace |
11,65 % |
A póker valószínűsége
A póker egy másik kártyajáték, ahol a valószínűség rendkívül fontos. Többek között. Nézzük tehát, milyen esélyeid vannak a pókerben.
Pre-flop valószínűség
Most, hogy felvázoltuk, hogyan működik a valószínűség egy kártyapakliban, térjünk rá a gyakorlati alkalmazásokra. Először is megmutatjuk, hogyan számolhatjuk ki annak a valószínűségét, hogy egy leosztásban elfogynak a párok. (például a sokat emlegetett ászok). Ebben az esetben a valószínűségeket meg kell szoroznunk egymással.
(4/52) x (3/51) = (12/2652) = (1/221) = 0,004524 (0,45 %)
📌 Megjegyzés: Ha egy olyan kaszinóban pókerezel, ahol óránként körülbelül 30 leosztás történik, akkor körülbelül 7 és fél óránként egyszer kapsz egy ászpárt.
Mennyi az esélye, hogy a 13 lehetséges pár közül bármelyiket megkapja, amikor osztja a lapokat? Feltételezhetjük, hogy az esély 1/221 az egyes párok esetében (lásd a fenti képletet). Összesen 13 ilyen pár lehet, így a számítási képlet 13/221=0,0588. Tehát körülbelül 35 meccsenként egyszer számíthatsz egy párra.
Valószínűség a pókerben játékos a játékos ellen
A póker azonban egy többszemélyes játék, általában egymás ellen játszanak. Íme egy válogatás a leggyakoribb pre-flop helyzetekből.
|
A kezed |
Az ellenfél keze |
A győzelem valószínűsége |
|
Magas pár |
Két alacsony lap |
83 % |
|
Magas pár |
Alacsony pár |
82 % |
|
Középső pár |
Magas, alacsony kártya |
71 % |
|
Két magas lap |
Két alacsony lap |
63 % |
|
Két magas lap |
Alacsony pár |
55 % |
A valószínűség kiszámítása "outs" alapján
Ha sikerül megnézned a lapokat a flopon, akkor minden bizonnyal még jobban érdekel, hogy milyen esélyeid vannak a kezed javítására. Ebben az esetben az úgynevezett "outs"-okról fogunk beszélni. A pókerben ez a kifejezés minden olyan kártyára utal, amely segíthet neked. Ilyen gyakori eset lehet, amikor egy játékosnak két lapja van egy színből, és a flopon megjelenik még két ugyanolyan színű lap. A játékosnak ekkor 4 lapja van a flösshöz, és így 9 kieső lapja van, így 9 lapja marad, amellyel flösst alkothat.
|
Kiesések száma |
Flop - Turn |
Turn - folyó |
Turn a River |
|
20 |
42,6 % |
43,5 % |
67,5 % |
|
19 |
40,4 % |
41,3 % |
65,0 % |
|
18 |
38,3 % |
39,1 % |
62,4 % |
|
17 |
36,2 % |
37,0 % |
59,8 % |
|
16 |
34,0 % |
34,8 % |
57,0 % |
|
15 |
31,9 % |
32,6 % |
54,1 % |
|
14 |
29,8 % |
30,4 % |
51,2 % |
|
13 |
27,7 % |
28,3 % |
48,1 % |
|
12 |
25,5 % |
26,1 % |
45,0 % |
|
11 |
23,4 % |
23,9 % |
41,7 % |
|
10 |
21,3 % |
21,7 % |
38,4 % |
|
9 |
19,1 % |
19,6 % |
35,0 % |
|
8 |
17,0 % |
17,4 % |
31,5 % |
|
7 |
14,9 % |
15,2 % |
27,8 % |
|
6 |
12,8 % |
13,0 % |
24,1 % |
|
5 |
10,6 % |
10,9 % |
20,3 % |
|
4 |
8,5 % |
8,7 % |
16,5 % |
|
3 |
6,4 % |
6,5 % |
12,5 % |
|
2 |
4,3 % |
4,3 % |
8,4 % |
|
1 |
2,1 % |
2,2 % |
4,3 % |
📌 Megjegyzés: Van egy nagyon egyszerű módszer az outok valószínűségének kiszámítására, így ezt közvetlenül az asztalnál is megteheted. Ezt általában "négy és kettő" szabálynak nevezik. A flop után a játékos egyszerűen megszorozza az outok számát 4-gyel, hogy megkapja a turn és a river valószínűségét. Ha nem kapja meg a lapot a turnön, akkor egyszerűen megszorozza az outok számát kettővel, hogy megkapja annak a hozzávetőleges valószínűségét, hogy megkapja a lapot a riveren.
Ismét használhatjuk azt a példát, amikor a flop után 4 azonos színű lapunk van. Tehát az outjaid 9 lap, és a turn és a river után a flöss valószínűsége 36% (9x4). Tegyük fel, hogy nem kapsz kártyát a fordulóban. Ebben az esetben megszorozzuk az outs-t kettővel, és azt kapjuk, hogy 18% (9x2) esélyünk van arra, hogy a riverre elfogynak a lapok ebben a színben. Mint a táblázat összehasonlításából látható, ez a módszer valóban egyszerű, de másrészt pontatlan, de használható.

 HU
HU  English
English  čeština
čeština  Polski
Polski  Slovenčina
Slovenčina  Русский
Русский  Deutsch
Deutsch  Slovenski
Slovenski  Dutch
Dutch  Svenska
Svenska  Português
Português  Italiano
Italiano  Español
Español  Français
Français  Suomalainen
Suomalainen  Български
Български  Românesc
Românesc  Eesti
Eesti  Ελληνική
Ελληνική  Latviešu
Latviešu  Lietuvių
Lietuvių  やまと
やまと  中国
中国  Dansk
Dansk  Türkçe
Türkçe  ID
ID  Українська
Українська  한국어
한국어  Norsk
Norsk 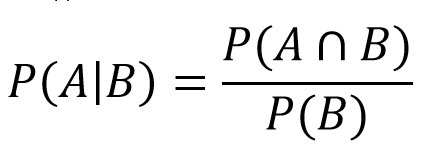


A hozzászóláshoz be kell jelentkezned