확률과 카지노 게임
 Peter Sommer
Peter Sommer
기회를 이해하셨나요? 카지노에서 게임을 하려면 자신의 기회를 알고 완벽하게 이해해야 합니다. 왜 그럴까요? 확률은 카지노를 작동시키는 엔진이기 때문입니다. 확률이 없다면 도박 산업은 불가능할 것입니다.
확률은 단순히 어떤 일이 일어날 확률입니다. 확률은 우리 일상 생활의 일부입니다. 빨간불에 번잡한 길을 건너려고 하면 차에 치일 가능성이 있지만, 그 대신 길을 더 빨리 건너고 여유 시간을 확보할 수 있는 기회가 생깁니다.
도박을 할 때 우리는 베팅을 공식화하기 위해 특정 이벤트가 발생할 확률을 추정합니다. 이러한 경우 확률을 계산합니다.
💡 확률 예시
4개의 공이 들어 있는 가방이 있는데 그 중 1개만 빨간색이고 나머지 3개는 파란색이라고 가정해 보겠습니다. 보지 않고 빨간 공만 뽑을 확률은 4분의 1입니다.
확률을 표현하는 방법에는 여러 가지가 있습니다. 또한 빨간색 공이 뽑힐 때마다 평균적으로 파란색 공 세 개를 뽑기 때문에 빨간색에 대한 확률은 3 대 1이라고 말할 수 있습니다.
확률을 백분율로 표현할 수도 있으므로 공이 뽑힐 확률이 100%인 경우 빨간색 공이 뽑힐 확률은 25%입니다. 따라서 100을 4로 나누면 25%가 됩니다.
25%의 확률로 파란색 공이 3개 있는 경우 파란색 공이 뽑힐 확률은 75%입니다.
카지노 게임 확률
카지노는 장기적인 결과를 고려할 때 그다지 좋지 않은 배당률을 제공한다는 원칙에 따라 운영됩니다.
풍선 봉지의 예는 카지노가 어떻게 작동하는지 보여주는 간단한 방법입니다. 카지노에서 빨간 공을 뽑는 데 3의 배당률을 제공한다고 가정해 보겠습니다. 5달러를 베팅하면 평균적으로 네 번의 시도에서 파란색 공을 세 번 뽑고 15달러를 잃고, 네 번째 시도에서 빨간색 공을 뽑고 10달러를 얻지만 카지노는 여전히 5달러의 흑자를 기록합니다.
모든 도박은 확률에 관한 것입니다. 경험 많은 도박꾼이라면
누구나 알 것입니다. 따라서 이러한 숫자에 익숙해지고 해당 숫자로 작업하는 방법을 아는 것이 중요합니다. 이제 도박에서 확률을 계산하는 방법을 보여드리겠습니다. 원리를 올바르게 이해하면 다른 어떤 것의 확률도 계산할 수 있습니다.
룰렛의 확률
룰렛은 행운의 바퀴와 같습니다. 그 이유가 뭔지 아세요? 큰수 이론은 단 세 단어로 설명할 수 있습니다. 카지노를 운영하거나 온라인 카지노 게임을 제작하는 모든 사람은 이 이론을 잘 알고 있습니다. 수입과 직결되기 때문입니다. 그리고 그 덕분에 카지노는 장기적으로도 항상 베터들을 이깁니다. 모든 것은 확률과 하우스 에지와 관련이 있습니다.
참고: 이 글의 모든 숫자는 유럽식 룰렛을 의미하므로 37개의 숫자를 세고 있습니다.
확률 작성 방법
확률을 작성하는 방법에는 여러 가지가 있습니다. 아마도 가장 잘 알려진 것은 백분율일 것입니다. 이 외에도 분수 또는 비율을 사용하는 표현식이 사용됩니다.
- 백분율(%)로 표시 - 여기에 추가할 내용은 많지 않지만 완성도를 높이기 위해 선택한 이벤트의 백분율입니다. (부분/총계)*100으로 계산됩니다. 예를 들어, 룰렛 휠에서 선택한 숫자를 맞출 확률(스트레이트): 1/37*100=2.7%
- 분수(1/x)를 사용한 표현 - 분수를 사용하여 확률을 표현할 때는 X번의 시도 중 1번의 현상이 발생한다고 말합니다. 숫자 표현에서는 백분율 계산에 의존합니다. 위의 1/37 예시를 고려하면 룰렛 휠에서 통계적으로 선택된 숫자가 37회 회전할 때 한 번 떨어질 확률이 높다는 뜻입니다.
- 비율별 표현식(x 대 1) - X가 발생할 때마다 선택한 현상이 1회 발생합니다. 여기에서도 룰렛에서 선택한 숫자에 대한 확률을 고수합니다. 이 경우 비율은 36대 1로 기록됩니다. 즉, 숫자가 떨어지지 않는 36번을 돌 때마다 선택한 숫자가 떨어지는 경우가 한 번씩 발생합니다.
참고: 큰수 이론에서 알 수 있듯이 확률은 본질적으로 수학적 한계입니다. 점점 더 많은 시도를 통해 현실적으로 계산된 결과에 점점 더 가까워집니다.
보시다시피 분수를 사용하는 표현식과 비율을 사용하는 표현식은 매우 유사합니다. 유일한 차이점은 분수는 모든 스핀을 계산하는 반면 비율은 총 스핀을 두 가지 범주로 나눈다는 점입니다.
룰렛의 개별 베팅에 대한 확률 표
|
베팅 |
에서 발췌 |
비율 |
백분율 |
|
스트레이트 베팅 |
1/2,055 |
1.055 대 1 |
48,6 % |
|
열 |
1/3,08 |
2.08대 1 |
32,4 % |
|
더 다스 |
1/3,08 |
2.08대 1 |
32,4 % |
|
여섯 줄 |
1/6,17 |
5.17대 1 |
16,2 % |
|
코너 |
1/9,25 |
8.25 대 1 |
10,8 % |
|
거리 |
1/12,33 |
11.33대 1 |
8,1 % |
|
분할 |
1/19,5 |
18.5 대 1 |
5,4 % |
|
스트레이트 |
1/37 |
36대 1 |
2,7 % |
스트레이트 베팅 확률
선택한 현상의 반복에 대한 수학적 비교도 흥미로울 수 있습니다. 이 경우에는 스트레이트 베팅, 특히 빨간색에 대한 베팅을 선택했습니다. 예를 들어 빨간색이 5번 연속으로 바뀔 확률은 어떻게 될까요?
|
회전 횟수 |
비율 |
백분율 |
|
1 |
1.06 대 1 |
48,6 % |
|
2 |
3.23 대 1 |
23,7 % |
|
3 |
7.69 대 1 |
11,5 % |
|
4 |
16.9대 1 |
5,6 % |
|
5 |
35.7 대 1 |
2,73 % |
|
6 |
74.4 대 1 |
1,33 % |
|
7 |
154 대 1 |
0,65 % |
|
8 |
318 대 1 |
0,31 % |
|
9 |
654 대 1 |
0,15 % |
|
10 |
1 346 대 1 |
0,074 % |
|
15 |
49 423 대 1 |
0,002 % |
|
20 |
1 813 778 대 1 |
0,000055 % |
보시다시피, 스핀 수가 증가함에 따라이 현상의 확률이 급격히 감소합니다. 그러나 이러한 확률은 현상 전체를 설명한다는 점을 명심하세요. 난수 생성기는 이전 결과를 고려하지 않으므로, 빨간색이 20번 연속으로 나오는 게임 시리즈가 181만 게임당 한 번씩 발생하더라도 21게임 라운드는 다른 모든 게임 라운드와 동일한 하우스 에지와 확률(즉, 48.6%)을 갖습니다.
이 경우 종종 플레이어의 오류라는 용어를 접할 수 있는데, 이는 베터가 한 색이 연속으로 여러 번 맞으면 다음 스핀에서 다른 색이 맞을 확률이 더 높다고 믿는 것입니다. 실제로는 그렇지 않습니다. 이 오류의 가장 유명한 사례는 1913년 몬테카를로 카지노에서 검은색이 룰렛 휠에 26번 연속으로 떨어졌을 때 관찰되었는데, 이 놀라운 연승이 계속되는 동안 거의 모든 사람들이 빨간색에 열광적으로 베팅을 했습니다. 그 때 카지노는 아주 큰 돈을 벌었습니다.
참고: 한 색상이 26번 연속으로 맞을 확률은 0.000000730870%이며, 6,700만 게임 중 한 번 발생합니다.
룰렛 확률을 계산하는 방법
개별 베팅에 대한 더 많은 배당률을 알고 싶으신가요? 직접 계산해 보세요. 백분율과 확률로 작업하는 것은 그리 복잡하지 않습니다. 일반적으로 가장 쉬운 방법은 분수로 시작하여 분수를 사용하여 추가 백분율과 비율을 계산하는 것입니다. 예를 들어 빨간색이 빨간색인 상황에 대한 확률을 분수로 계산하려면 다음과 같이 하면 됩니다:
경기장에 있는 총 빨간색 수/총 경기장 수 = 18/37
한 번의 스핀에 대한 확률
여기에도 간단한 규칙이 적용됩니다. 당첨이 가능한 필드 수를 계산하고 이를 전체 필드 수로 나누기만 하면 됩니다.
예를 들어
- 색상 - 18/37
- 수다/리차 - 18/37
- 다스 - 12/37
- 숫자 0 - 1/37
- 검은색과 짝수 - 9/37(경기장에 검은색과 짝수인 숫자는 9개뿐입니다)
- 다스 및 열 - 4/37(다스 및 열에는 4개의 숫자만 있음)
승리 확률과 마찬가지로 패배 확률도 계산할 수 있습니다. 당첨되지 않은 필드의 수를 세고 이를 다시 전체 필드 수로 나누면 됩니다. 예를 들어, 빨간색에 베팅할 경우 패배할 확률은 19/37(검은색 필드 18개 + 녹색 0)입니다.
참고: 분수를 1/x로 줄이려면 분자와 분모를 분모로 나누기만 하면 됩니다. 예를 들어 18/37(두 숫자를 18로 나눈 값)은 조정 후 1/2.055가 됩니다. 즉, 2.055회 턴할 때마다 한 턴씩 빨간색 또는 검은색으로 표시됩니다.
다중 스핀에 대한 확률
단일 스핀에 대한 계산을 마스터하고 나면 다중 스핀에 대한 확률을 계산하는 것은 매우 간단합니다. 개별 분수에 서로 곱하기만 하면 됩니다.
예시:
- 스핀 - 빨간색에 베팅 = 18/37
- 스핀 - 다스당 베팅 = 12/37
두 라운드 모두 승리할 확률 = (18/37)*(12/37)=1/6.34 또는 15.77% 또는 5.34대 1
- 스핀 - 스트레이트 베팅 - 1/37
- 스핀 - 스트레이트 베팅 - 1/37
두 라운드 모두 승리할 확률 = (1/37)*(1*37)=1/1369 또는 0.073% 또는 1368대 1
- 스핀 - 검은색과 홀수 9/37에 베팅하세요.
- 스핀 - 짝수 18/37에 베팅
- 스핀 - 컬럼 베팅 12/37
3라운드 모두 승리할 확률 = (9/37)*(18/37)*(12/37)=1/26.06 또는 3.84% 또는 25.06대 1
항목 간의 실제 변환은 다시 매우 쉽습니다. 분수를 1/x 형식으로 나눈 다음 100을 곱하면 백분율을 구할 수 있습니다. 총합의 우승 라운드인 분모에서 1을 빼면 X에서 1의 형태로 비례 표기가 됩니다. 단락 위의 예시를 참조하세요.
주사위 확률
크랩스는 비교적 쉽게 확률을 계산할 수 있는 또 다른 우연 게임입니다. 크랩스 게임에서 승리할 확률을 계산하기 전에 주사위를 굴릴 확률 자체를 살펴보겠습니다.
주사위는 6면이 있습니다. 따라서 어떤 숫자가 떨어질 확률은 1/6입니다. 크랩스는 전통적으로 두 개의 주사위로 플레이합니다. 따라서 두 숫자가 결합할 확률은 2/36입니다. 하지만 크랩스에서는 특정 숫자보다는 그 숫자의 합이 훨씬 더 중요합니다. 다시 한 번, 당첨 조합 수/모든 조합 수라는 공식을 사용하겠습니다.
7의 합에 대한 확률을 알고 싶다고 가정해 보겠습니다. 당첨 조합: (1-6), (2-4), (3-3), (4-2), (6-1). 보시다시피, 두 개의 주사위를 굴려 7의 합이 나올 수 있는 조합은 총 6가지가 있습니다. 그리고 모든 조합의 수가 36이므로 7의 확률은 6/36=0.1666입니다.
이러한 방식으로 다른 모든 가능한 결과를 쉽게 계산할 수 있습니다.
|
합계 |
확률 |
|
2 |
1/36 |
|
3 |
2/36 |
|
4 |
3/36 |
|
5 |
4/36 |
|
6 |
5/36 |
|
7 |
6/36 |
|
8 |
5/36 |
|
9 |
4/36 |
|
10 |
3/36 |
|
11 |
2/36 |
|
12 |
1/36 |
크랩스에서 승리할 확률
주사위 규칙을 간단히 살펴봅시다. 가장 일반적인 베팅은 패스 라인입니다.
- 7 또는 11을 굴리면 승리합니다.
- 2, 3 또는 12를 굴리면 패배합니다.
- 그 외의 경우(4, 5, 6, 8, 9, 10)에는 1점을 결정하고 해당 점수가 다시 굴려지거나(승리) 7이 굴려질 때까지(패배) 굴립니다.
포인트를 결정하기 전에 먼저 당첨 확률을 계산합니다. 7을 맞출 확률은 6/36이고 11을 맞출 확률은 2/36입니다. 그런 다음 이 두 분수를 더하여 3/36+2/36 = 2/9 = 0.2222를 구해야 합니다.
이제 포인트가 결정되는 상황을 살펴보겠습니다. 즉, 포인트가 4, 5, 6, 8, 9 또는 10인 경우입니다. 총 4개부터 시작하겠습니다.
4가 나오면 1점이 결정되고 플레이어는 4 또는 7이 나올 때까지 굴립니다. 여기서 우리는 조건부 확률의 영역으로 들어갑니다. 이는 이벤트 B가 동시에 발생할 경우 이벤트 A가 발생할 확률이 얼마인지 알려줍니다. 우리의 경우, 라운드가 끝날 때(4 또는 7을 굴릴 때) 이길 확률(4를 굴릴 확률)이 될 것입니다. 그런 다음 이 값을 수식에 연결합니다:
- P(A) = 4의 낙하 합계: 3/36
- P(A∩B) = 조정 후 A와 같다는 것을 알 수 있습니다.
- P(B) = 낙하 4 또는 7: 3/36 + 6/36 = 9/36
그다음은 다음과 같습니다:
- P(4|4 또는 7) = (3/36)/(9/36) = 1/3
비슷한 방법으로 5, 6, 8, 9, 10의 합을 계산할 수 있습니다.
- P(5|5 또는 7) = (4/36)/(10/36) = 2/5
- P(6|6 또는 7) = (5/36)/(11/36) = 5/11
- P(8|8 또는 7) = (5/36)/(11/36) = 5/11
- P(9|9 또는 7) = (4/36)/(10/36) = 2/5
- P(10|10 또는 7) = (3/36)/(9/36) = 1/3
이제 점수가 결정된 첫 번째 롤과 플레이어가 승리한 다음 롤의 확률로 승리 확률을 계산할 수 있습니다.
- 원본 롤 4 x P(4|4 또는 7) = 3/36 x 1/3 = 1/36
- 원본 롤 5 x P(5|5 또는 7) = 4/36 x 2/5 = 2/45
- 원본 롤 6 x P(6|6 또는 7) = 5/36 x 5/11 = 25/396
- 원본 롤 8 x P(8|8 또는 7) = 5/36 x 5/11 = 25/396
- 원본 롤 9 x P(9|9 또는 7) = 4/36 x 2/5 = 2/45
- 원본 롤 10 x P(10|10 또는 7) = 3/36 x 1/3 = 1/36
이 모든 분수는 첫 번째 롤이 4, 5, 6, 8, 9 또는 10인 경우 당첨 확률을 알려줍니다. 패스 라인 베팅의 총 당첨 확률을 알고 싶으시다면, 이 모든 확률을 합산한 후 포인트 이전의 당첨 확률(7 또는 11을 굴려 2/9)을 더하면 됩니다.
2/9 + 1/36 + 2/45 + 25/396 + 25/396 + 2/45 + 1/36 = 244/495
244/495는 정확히 49.3%이기 때문입니다. 이는 50%에 조금 못 미치는 수치입니다. 사실, 1 대 1의 배당금으로 이보다 더 좋은 당첨 확률을 찾을 수는 없을 것입니다. 카드를 셀 수 있다면 블랙잭만 빼고요.
블랙잭 확률
블랙잭은 확률이 가장 중요한 우연의 게임입니다. 블랙잭에서는 실력과 지식으로 하우스 에지에 영향을 줄 수 있습니다. 이를 위한 최적의 전략만 알면 되고, 카드 세는 법만 알면 플레이어가 유리하게 플레이할 수도 있습니다. 이 모든 계산은 블랙잭의 모든 전술과 전략을 고안한 수학자들이 이미 수행한 것이기 때문에 실제로 모든 구체적인 확률을 알 필요는 없습니다.
그러나 흥미를 위해 블랙잭에서 몇 가지 중요한 현상에 대한 확률을 계산하는 방법을 보여 드리겠습니다.
확률의 문제를 카드 한 벌의 관점에서 보면 가능한 결과의 수가 급격히 증가한다는 것을 알 수 있습니다. 블랙잭은 52장의 카드, 4개의 수트, 13개의 밸류로 구성된 덱으로 플레이합니다. 이렇게 하면 다음과 같은 확률이 나옵니다:
- 덱(또는 개별 카드)에서 에이스를 뽑을 경우: 4/52=0.0769 (7.69%)
- 덱에서 스페이드를 뽑습니다: 13/52=0.25 (25%)
하지만 동전 던지기, 룰렛, 슬롯머신과 달리 카드 한 벌에는 '기억'이라는 것이 있습니다. 즉, 이전 결과가 현재와 미래의 움직임에 영향을 미친다는 뜻입니다. 이는 카드가 덱에서 떨어졌고 이로 인해 시작 상황이 변경되었기 때문입니다. 52장의 카드 덱에서 첫 번째 카드로 에이스가 뽑힌 경우(7.69% 확률)를 예로 들어 보겠습니다. 이제 덱에서 두 번째 카드로 에이스가 다시 뽑힐 확률은 달라집니다. 첫 번째 무승부 후 에이스의 수는 3개로, 카드의 수는 51장으로 감소했습니다.
블랙잭 내추럴 확률
모든 플레이어가 가장 먼저 관심을 갖는 것은 블랙잭 확률입니다. 즉, 플레이어가 라운드 시작과 동시에 에이스와 10장의 카드를 얻을 확률은 얼마나 되는지, 다시 말해 자연스러운 현상입니다.
이 상황은 두 가지 방식으로 발생할 수 있으며, 두 가지 방식을 더하면 블랙잭에 대한 확률을 알 수 있습니다:
참고: 저희는 싱글 덱 블랙잭을 계산하고 있습니다. 카드 52장, 에이스 4장, 텐 16장이네요. 딜러의 카드는 보이지 않으므로 확률에 영향을 미치지 않습니다.
- 플레이어는 첫 번째 에이스와 10장의 카드를 받습니다.
플레이어는 4/52의 확률로 첫 번째 에이스 카드를 받습니다. 따라서 플레이어는 10이 있는 두 번째 카드를 가져와야 하며, 그 확률은 16/51입니다. 이 두 확률을 서로 곱하면 16/663이 됩니다.
- 플레이어는 처음 10장의 카드와 에이스를 받습니다.
플레이어가 값이 10인 첫 번째 카드를 받을 확률은 16/52입니다. 그 이후 플레이어가 에이스를 획득할 확률은 4/51입니다. 곱하면 16/663이 됩니다.
블랙잭이 나올 확률을 알고 싶다면 이 두 가지 현상을 더하면 됩니다. 따라서 16/663 + 16/663 = 32/663 = 4.827%입니다. 즉, 플레이어는 약 20핸드에 한 번씩 블랙잭을 받게 됩니다. 비슷한 방법으로 멀티덱 테이블의 확률을 계산할 수 있으며, 이미 계산해 드린 바 있습니다.
|
패키지 수 |
확률 |
|
1 |
4,827 % |
|
2 |
4,780 % |
|
3 |
4,764 % |
|
4 |
4,757 % |
|
5 |
4,752 % |
|
6 |
4,749 % |
흉상 확률
실패 확률이 얼마나 되는지 알아보는 것도 흥미로울 수 있습니다. 다시 한 번, 싱글 덱 테이블에서 딜러와 단둘이 플레이하는 상황을 예로 들어보겠습니다. 플레이어가 총 10의 가치가 있는 카드 2장을 가지고 있어 20점을 가지고 있는 아주 간단한 상황을 살펴보겠습니다. 플레이어가 세 번째 카드를 받는 상황에서는 덱에서 이미 3장의 카드가 나온 상태입니다. 이렇게 하면 덱에 49장의 카드가 남습니다. 49장의 카드 중 에이스는 4장뿐입니다. 이 49개 중 45개는 원치 않는 카드입니다. 따라서 흉상 확률은 45/49=0.9183673입니다.
비슷한 방법으로 다른 확률도 계산할 수 있습니다. 항상 상황을 정확하게 상상할 수 있어야 합니다. 그게 다입니다.
|
손의 가치 |
흉상 발생 확률 |
|
21 |
100 % |
|
20 |
92 % |
|
19 |
85 % |
|
18 |
77 % |
|
17 |
69 % |
|
16 |
62 % |
|
15 |
58 % |
|
14 |
56 % |
|
13 |
39 % |
|
12 |
31 % |
|
11 덜 |
0 % |
이제 딜러가 각 카드에 대해 얼마나 높은 확률로 버스트할 수 있는지 살펴보겠습니다.
|
손의 가치 |
흉상 발생 확률 |
|
2 |
35,30 % |
|
3 |
37,56 % |
|
4 |
40,28 % |
|
5 |
42,89 % |
|
6 |
42,08 % |
|
7 |
25,99 % |
|
8 |
23,86 % |
|
9 |
23,34 % |
|
10, J, Q, K |
21,43 % |
|
에이스 |
11,65 % |
포커 확률
포커는 확률이 매우 중요한 또 다른 카드 게임입니다. 무엇보다도. 이제 포커에서 어떤 기회가 있는지 살펴봅시다.
프리 플랍 확률
이제 카드 한 장에서 확률이 어떻게 작동하는지에 대해 간략하게 설명했으니 실제 적용에 대해 알아보겠습니다. 우선, 한 쌍이 부족할 확률(예를 들어, 많이 언급되는 에이스)을 계산하는 방법을 보여드리겠습니다. 이 경우 확률을 서로 곱해야 합니다.
(4/52) x (3/51) = (12/2652) = (1/221) = 0,004524 (0,45 %)
참고: 시간당 약 30개의 핸드를 취급하는 카지노에서 포커를 플레이하는 경우, 약 7시간 반에 한 번씩 에이스 한 쌍을 받게 됩니다.
그렇다면 거래할 때 13개의 가능한 쌍 중 어떤 쌍을 얻을 확률은 얼마나 될까요? 개별 쌍당 확률은 1/221이라고 가정할 수 있습니다(위 공식 참조). 이러한 쌍은 총 13개가 있을 수 있으므로 계산 공식은 13/221=0.0588이 됩니다. 따라서 35경기에 한 번씩 한 쌍을 기대할 수 있습니다.
포커 플레이어 대 플레이어의 확률
하지만 포커는 보통 서로 대결하는 멀티플레이어 게임입니다. 다음은 가장 일반적인 프리 플랍 상황의 예시입니다.
|
손 |
상대의 손 |
당첨 확률 |
|
하이 페어 |
낮은 카드 두 장 |
83 % |
|
하이 페어 |
로우 페어 |
82 % |
|
가운데 쌍 |
높음, 낮음 카드 |
71 % |
|
높은 카드 두 장 |
낮은 카드 두 장 |
63 % |
|
높은 카드 두 장 |
로우 페어 |
55 % |
"아웃"에 의한 확률 계산
플롭에서 카드를 볼 수 있다면 핸드가 향상될 가능성에 대해 더 많은 관심을 갖게 될 것입니다. 이 경우 소위 "아웃"에 대해 이야기하겠습니다. 포커에서 이 용어는 도움이 될 수 있는 모든 카드를 의미합니다. 플레이어가 한 세트에 두 장의 카드를 보유하고 있는데 플랍에 같은 세트의 카드 두 장이 더 나오는 경우가 이에 해당합니다. 그러면 플레이어는 플러시할 카드가 4장이므로 9장의 아웃이 발생하여 플러시를 형성할 카드가 9장이 남습니다.
|
아웃 횟수 |
플롭 - 턴 |
회전 - 강 |
강을 돌리다 |
|
20 |
42,6 % |
43,5 % |
67,5 % |
|
19 |
40,4 % |
41,3 % |
65,0 % |
|
18 |
38,3 % |
39,1 % |
62,4 % |
|
17 |
36,2 % |
37,0 % |
59,8 % |
|
16 |
34,0 % |
34,8 % |
57,0 % |
|
15 |
31,9 % |
32,6 % |
54,1 % |
|
14 |
29,8 % |
30,4 % |
51,2 % |
|
13 |
27,7 % |
28,3 % |
48,1 % |
|
12 |
25,5 % |
26,1 % |
45,0 % |
|
11 |
23,4 % |
23,9 % |
41,7 % |
|
10 |
21,3 % |
21,7 % |
38,4 % |
|
9 |
19,1 % |
19,6 % |
35,0 % |
|
8 |
17,0 % |
17,4 % |
31,5 % |
|
7 |
14,9 % |
15,2 % |
27,8 % |
|
6 |
12,8 % |
13,0 % |
24,1 % |
|
5 |
10,6 % |
10,9 % |
20,3 % |
|
4 |
8,5 % |
8,7 % |
16,5 % |
|
3 |
6,4 % |
6,5 % |
12,5 % |
|
2 |
4,3 % |
4,3 % |
8,4 % |
|
1 |
2,1 % |
2,2 % |
4,3 % |
참고: 테이블에서 바로 계산할 수 있는 매우 쉬운 아웃 확률을 계산하는 방법이 있습니다. 일반적으로 이를 "4와 2" 규칙이라고 합니다. 플랍이 끝나면 플레이어는 아웃의 수에 4를 곱하여 턴과 리버의 확률을 찾습니다. 턴에 카드를 얻지 못하면 아웃의 수에 2를 곱하여 리버에 카드를 얻을 대략적인 확률을 구합니다.
플랍 후 같은 수트의 카드 4장을 가지고 있는 경우를 다시 예로 들어보겠습니다. 따라서 아웃은 9장이고 턴과 리버 후 플러시 확률은 36%(9x4)입니다. 턴에 카드를 받지 못했다고 가정해 보겠습니다. 이 경우 아웃에 2를 곱하면 리버에 있는 수트의 카드가 부족할 확률이 18%(9x2)라는 것을 알 수 있습니다. 표를 비교해보면 알 수 있듯이 이 방법은 매우 간단하지만 부정확하지만 사용할 수 있습니다.

 KO
KO  English
English  čeština
čeština  Polski
Polski  Slovenčina
Slovenčina  Русский
Русский  Deutsch
Deutsch  Slovenski
Slovenski  Dutch
Dutch  Svenska
Svenska  Português
Português  Italiano
Italiano  Español
Español  Français
Français  Suomalainen
Suomalainen  Български
Български  Românesc
Românesc  Magyar
Magyar  Eesti
Eesti  Ελληνική
Ελληνική  Latviešu
Latviešu  Lietuvių
Lietuvių  やまと
やまと  中国
中国  Dansk
Dansk  Türkçe
Türkçe  ID
ID  Українська
Українська  Norsk
Norsk 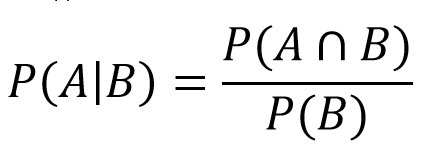


댓글을 추가하려면 로그인 상태여야 합니다.