Πιθανότητα και παιχνίδια καζίνο
 Peter Sommer
Peter Sommer
Καταλαβαίνετε τις πιθανότητές σας; Εάν πρόκειται να παίξετε σε ένα καζίνο, θα πρέπει να βεβαιωθείτε ότι γνωρίζετε τις πιθανότητές σας και ότι τις κατανοείτε απόλυτα. Γιατί; Επειδή η πιθανότητα είναι η μηχανή που κάνει τα καζίνο να λειτουργούν. Χωρίς τις πιθανότητες, η βιομηχανία τυχερών παιχνιδιών δεν θα ήταν δυνατή.
Η τύχη είναι απλώς η πιθανότητα να συμβεί κάτι. Οι πιθανότητες είναι μέρος της καθημερινής μας ζωής. Όταν αποφασίζουμε να διασχίσουμε έναν πολυσύχναστο δρόμο με κόκκινο φανάρι, υπάρχει κάποια πιθανότητα να μας χτυπήσει αυτοκίνητο, αλλά σε αντάλλαγμα έχουμε την ευκαιρία να διασχίσουμε το δρόμο πιο γρήγορα και να κερδίσουμε λίγο χρόνο.
Όταν παίζουμε τυχερά παιχνίδια, εκτιμούμε την πιθανότητα να συμβεί ένα συγκεκριμένο γεγονός, προκειμένου να διαμορφώσουμε το στοίχημά μας. Σε αυτές τις περιπτώσεις υπολογίζουμε την πιθανότητα.
💡 Παράδειγμα πιθανότητας
Ας υποθέσουμε ότι έχουμε μια σακούλα που περιέχει τέσσερις μπάλες από τις οποίες μόνο η μία είναι κόκκινη και οι άλλες τρεις είναι μπλε. Η πιθανότητα να τραβήξετε μόνο την κόκκινη μπάλα χωρίς να κοιτάξετε είναι 1 προς 4.
Υπάρχουν διάφοροι τρόποι για να εκφραστεί η πιθανότητα. Μπορούμε επίσης να πούμε ότι υπάρχει μια πιθανότητα 3 προς 1 έναντι του κόκκινου, επειδή κατά μέσο όρο τραβάμε τρεις μπλε μπάλες για κάθε κόκκινη μπάλα που τραβάμε.
Μπορούμε επίσης να εκφράσουμε τις πιθανότητές μας ως ποσοστό, οπότε η πιθανότητα να τραβήξουμε μια κόκκινη μπάλα είναι 25% αν υπάρχει 100% πιθανότητα να τραβήξουμε μια μπάλα. Έτσι το 100 διαιρούμενο με το τέσσερα μας δίνει 25%.
Η πιθανότητα να τραβήξετε μια μπλε μπάλα είναι 75% αν υπάρχουν τρεις μπλε μπάλες με 25% πιθανότητα να τραβήξετε.
Πιθανότητα παιχνιδιών καζίνο
Το καζίνο λειτουργεί με βάση την αρχή της προσφοράς αποδόσεων που δεν είναι τόσο καλές σε σχέση με το μακροπρόθεσμο αποτέλεσμά μας.
Το παράδειγμα μιας σακούλας με μπαλόνια είναι ένας απλός τρόπος να δείξουμε πώς λειτουργεί ένα καζίνο. Ας υποθέσουμε ότι ένα καζίνο προσφέρει απόδοση 3 για να τραβήξετε μια κόκκινη μπάλα. Αν ποντάρετε 5 δολάρια, τότε κατά μέσο όρο, σε τέσσερις προσπάθειες θα τραβήξετε την μπλε μπάλα σας 3 φορές και θα χάσετε 15 δολάρια, και την τέταρτη φορά θα τραβήξετε την κόκκινη μπάλα σας και θα κερδίσετε 10 δολάρια, αλλά το καζίνο θα εξακολουθεί να είναι με 5 δολάρια στα μαύρα. Όλα τα τυχερά παιχνίδια αφορούν μόνο τις πιθανότητες. Κάθε έμπειρος παίκτης θα σας το πει αυτό. Επομένως, είναι απαραίτητο να είστε εξοικειωμένοι με αυτούς τους αριθμούς και να ξέρετε πώς να εργάζεστε με αυτούς. Εδώ λοιπόν θα σας δείξουμε τώρα πώς να υπολογίζετε την πιθανότητα στα τυχερά παιχνίδια. Αν κατανοήσετε σωστά την αρχή, μπορείτε να τη χρησιμοποιήσετε για να υπολογίσετε την πιθανότητα για οτιδήποτε άλλο.
Πιθανότητα στη ρουλέτα
Η ρουλέτα είναι σαν τον Τροχό της Τύχης. Και ξέρετε γιατί; Χρειάζονται μόνο 3 λέξεις για να εξηγηθεί - Θεωρία των Μεγάλων Αριθμών. Κάθε άτομο που διευθύνει ένα καζίνο ή παράγει online παιχνίδια καζίνο γνωρίζει πολύ καλά αυτή τη θεωρία. Επειδή συνδέεται άμεσα με τις αποδοχές του. Και χάρη σε αυτό, το καζίνο κερδίζει πάντα τους παίκτες του στοιχήματος μακροπρόθεσμα. Τα πάντα συνδέονται με την πιθανότητα και το πλεονέκτημα του σπιτιού.
📌 Σημείωση: Όλοι οι αριθμοί στο άρθρο αναφέρονται στην ευρωπαϊκή ρουλέτα - έτσι μετράμε 37 αριθμούς.
Πώς να γράψετε πιθανότητα
Υπάρχουν διάφοροι τρόποι για να γράψετε την πιθανότητα. Πιθανώς το πιο γνωστό είναι τα ποσοστά. Εκτός από αυτά, χρησιμοποιούνται και εκφράσεις που χρησιμοποιούν κλάσμα ή αναλογία.
- Εκφράζεται ως ποσοστό (%) - δεν υπάρχουν πολλά να προστεθούν εδώ, αλλά για λόγους πληρότητας, αυτό είναι το ποσοστό για το επιλεγμένο συμβάν. Υπολογίζεται ως (Μέρος/Σύνολο)*100. Για παράδειγμα, η πιθανότητα να πετύχετε τον επιλεγμένο αριθμό σε μια ρουλέτα (ευθεία): 1/37*100=2,7%.
- Έκφραση με χρήση κλασμάτων (1/x) - Όταν εκφράζουμε την πιθανότητα με χρήση κλάσματος, λέμε ότι το φαινόμενο συμβαίνει 1 φορά σε Χ δοκιμές. Στην αριθμητική έκφραση, βασιζόμαστε στον υπολογισμό ποσοστών. Αν θεωρήσουμε το παράδειγμα 1/37 παραπάνω, αυτό σημαίνει ότι ένας στατιστικά επιλεγμένος αριθμός στον τροχό της ρουλέτας θα πέσει 1 φορά σε 37 περιστροφές.
- Έκφραση με αναλογία (x προς 1) - Κάθε φορά που συμβαίνει το Χ, το επιλεγμένο φαινόμενο συμβαίνει 1 φορά. Και εδώ πάλι παραμένουμε στην πιθανότητα για τον επιλεγμένο αριθμό στη ρουλέτα. Στην περίπτωση αυτή, η αναλογία θα γραφτεί ως 36 προς 1. Αυτό σημαίνει ότι μετά από κάθε 36 περιστροφές όπου ο αριθμός δεν πέφτει, θα υπάρχει μία περίπτωση όπου ο επιλεγμένος αριθμός πέφτει.
📌 Σημείωση: Όπως λέει η θεωρία των μεγάλων αριθμών, η πιθανότητα είναι ουσιαστικά ένα μαθηματικό όριο. Με όλο και περισσότερες δοκιμές, ρεαλιστικά πλησιάζετε όλο και περισσότερο στο υπολογισμένο αποτέλεσμα.
Όπως μπορείτε να δείτε, οι εκφράσεις που χρησιμοποιούν κλάσματα και οι εκφράσεις που χρησιμοποιούν αναλογίες είναι πολύ παρόμοιες. Η μόνη διαφορά είναι ότι το κλάσμα μετράει όλες τις περιστροφές, ενώ η αναλογία χωρίζει τις συνολικές περιστροφές σε δύο κατηγορίες.
Πίνακας πιθανοτήτων για μεμονωμένα στοιχήματα στη ρουλέτα
|
Στοίχημα |
Απόσπασμα από |
Αναλογία |
Ποσοστά |
|
Ένα ευθύ στοίχημα |
1/2,055 |
1,055 προς 1 |
48,6 % |
|
Στήλη |
1/3,08 |
2,08 προς 1 |
32,4 % |
|
Η δωδεκάδα |
1/3,08 |
2,08 προς 1 |
32,4 % |
|
Έξι γραμμές |
1/6,17 |
5,17 προς 1 |
16,2 % |
|
Γωνία |
1/9,25 |
8,25 προς 1 |
10,8 % |
|
Οδός |
1/12,33 |
11,33 προς 1 |
8,1 % |
|
Split |
1/19,5 |
18,5 προς 1 |
5,4 % |
|
Ευθεία |
1/37 |
36 προς 1 |
2,7 % |
Πιθανότητα για ένα straight στοίχημα
Μια μαθηματική σύγκριση για την επανάληψη του επιλεγμένου φαινομένου θα μπορούσε επίσης να είναι ενδιαφέρουσα. Για την περίπτωση αυτή έχουμε επιλέξει ένα ευθύ στοίχημα, συγκεκριμένα για παράδειγμα ένα στοίχημα στο κόκκινο. Ποια θα είναι λοιπόν η πιθανότητα αλλαγής του κόκκινου χρώματος 5 φορές στη σειρά, για παράδειγμα;
|
Αριθμός περιστροφών |
Αναλογία |
Ποσοστά |
|
1 |
1,06 προς 1 |
48,6 % |
|
2 |
3,23 προς 1 |
23,7 % |
|
3 |
7,69 προς 1 |
11,5 % |
|
4 |
16,9 προς 1 |
5,6 % |
|
5 |
35,7 προς 1 |
2,73 % |
|
6 |
74,4 προς 1 |
1,33 % |
|
7 |
154 προς 1 |
0,65 % |
|
8 |
318 προς 1 |
0,31 % |
|
9 |
654 προς 1 |
0,15 % |
|
10 |
1 346 προς 1 |
0,074 % |
|
15 |
49 423 προς 1 |
0,002 % |
|
20 |
1 813 778 έως 1 |
0,000055 % |
Όπως φαίνεται, καθώς αυξάνεται ο αριθμός των σπιν, η πιθανότητα αυτού του φαινομένου μειώνεται ραγδαία. Ωστόσο, να έχετε κατά νου ότι αυτές οι πιθανότητες περιγράφουν το φαινόμενο στο σύνολό του. Η γεννήτρια τυχαίων αριθμών δεν λαμβάνει υπόψη τα προηγούμενα αποτελέσματα, επομένως, ακόμη και αν μια σειρά παιχνιδιών όπου το κόκκινο χτυπάει 20 φορές στη σειρά συμβαίνει μία φορά κάθε 1,813 εκατομμύρια παιχνίδια, ένας γύρος 21 παιχνιδιών θα έχει το ίδιο πλεονέκτημα και την ίδια πιθανότητα (δηλαδή 48,6%) με κάθε άλλο γύρο παιχνιδιών.
Συχνά σε αυτή την περίπτωση, μπορεί κανείς να συναντήσει τον όρο πλάνη του παίκτη, όπου ο παίκτης πιστεύει ότι αν ένα χρώμα χτυπηθεί πολλές φορές στη σειρά, υπάρχει μεγαλύτερη πιθανότητα να χτυπηθεί το άλλο χρώμα στην επόμενη περιστροφή. Στην πραγματικότητα, αυτό δεν ισχύει. Η πιο διάσημη περίπτωση αυτής της πλάνης παρατηρήθηκε το 1913 στο καζίνο του Μόντε Κάρλο, όταν το μαύρο έπεσε 26 φορές στη σειρά στον τροχό της ρουλέτας και σχεδόν καθ' όλη τη διάρκεια αυτού του απίστευτου σερί, αλλά και μετά το τέλος του, οι άνθρωποι πόνταραν μανιωδώς στο κόκκινο. Τότε ήταν που το καζίνο έβγαλε μερικά πολύ ωραία χρήματα.
📌 Σημείωση: Η πιθανότητα ένα χρώμα να χτυπηθεί 26 φορές στη σειρά είναι 0,000000730870% και συμβαίνει μία φορά σε 67 εκατομμύρια παιχνίδια.
Πώς να υπολογίσετε την πιθανότητα της ρουλέτας
Θέλετε να μάθετε περισσότερες αποδόσεις για μεμονωμένα στοιχήματα; Προσπαθήστε να τα υπολογίσετε μόνοι σας. Η εργασία με ποσοστά και πιθανότητες δεν είναι πολύ περίπλοκη. Γενικά, ο ευκολότερος τρόπος είναι να ξεκινήσετε με κλάσματα και να τα χρησιμοποιήσετε για να υπολογίσετε περαιτέρω ποσοστά και αναλογίες. Για παράδειγμα, αν θέλετε να υπολογίσετε την πιθανότητα σε ένα κλάσμα για μια κατάσταση όπου το κόκκινο είναι κόκκινο, κάνετε τα εξής:
Συνολικός αριθμός κόκκινων στον αγωνιστικό χώρο/συνολικός αριθμός αγωνιστικών χώρων = 18/37
Πιθανότητα για μία περιστροφή
Και πάλι, εδώ ισχύει ένας απλός κανόνας. Απλά υπολογίστε τον αριθμό των πεδίων που θα σας δώσουν ένα κέρδος και διαιρέστε τον με τον συνολικό αριθμό των πεδίων.
Για παράδειγμα:
- Χρώμα - 18/37
- Sudá/Lichá - 18/37
- Δωδεκάδα - 12/37
- Αριθμός 0 - 1/37
- Μαύρος και ζυγός - 9/37 (υπάρχουν μόνο 9 αριθμοί στο πεδίο παιχνιδιού που είναι και μαύροι και ζυγοί)
- Δωδεκάδα και στήλη - 4/37 (υπάρχουν μόνο 4 αριθμοί σε μια δωδεκάδα και σε μια στήλη)
Ακριβώς όπως η πιθανότητα να κερδίσετε, μπορείτε να υπολογίσετε την πιθανότητα να χάσετε. Απλά μετρήστε τον αριθμό των πεδίων που δεν κέρδισαν και διαιρέστε τα πάλι με τον συνολικό αριθμό των πεδίων. Για παράδειγμα, η πιθανότητα να χάσετε αν ποντάρετε στο κόκκινο είναι 19/37 (18 μαύρα πεδία + πράσινο μηδέν).
📌 Σημείωση: Για να μειώσετε ένα κλάσμα σε 1/x, απλά διαιρέστε τον αριθμητή και τον παρονομαστή με τον αριθμητή. Για παράδειγμα, το 18/37 (διαιρείτε και τους δύο αριθμούς με το 18) θα είναι 1/2,055 μετά την προσαρμογή. Αυτό σημαίνει ότι για κάθε 2,055 στροφές, μία στροφή θα έχει ως αποτέλεσμα ένα κόκκινο ή ένα μαύρο.
Πιθανότητα για πολλαπλές περιστροφές
Μόλις μάθετε τον υπολογισμό για μεμονωμένες περιστροφές, ο υπολογισμός της πιθανότητας για πολλαπλές περιστροφές είναι πολύ απλός. Απλώς πολλαπλασιάστε τα επιμέρους κλάσματα μεταξύ τους.
Παραδείγματα:
- περιστροφή - ποντάρισμα στο κόκκινο = 18/37
- περιστροφή - ποντάρισμα ανά δωδεκάδα = 12/37
Πιθανότητα νίκης και στους δύο γύρους = (18/37)*(12/37)=1/6,34 ή 15,77% ή 5,34 προς 1
- περιστροφή - στοίχημα ευθείας - 1/37
- περιστροφή - στοίχημα ευθείας - 1/37
Πιθανότητα νίκης και στους δύο γύρους = (1/37)*(1*37)=1/1369 ή 0,073% ή 1368 προς 1
- περιστροφή - ποντάρισμα σε μαύρο και μονό 9/37
- περιστροφή - ποντάρετε σε ζυγό 18/37
- περιστροφή - στοίχημα στήλης 12/37
Πιθανότητα νίκης και στους 3 γύρους = (9/37)*(18/37)*(12/37)=1/26,06 ή 3,84% ή 25,06 προς 1
Η πραγματική μετατροπή μεταξύ των καταχωρίσεων είναι και πάλι πολύ εύκολη. Τα ποσοστά προκύπτουν διαιρώντας το κλάσμα με τη μορφή 1/x και στη συνέχεια πολλαπλασιάζοντας με το 100. Παίρνετε τον αναλογικό συμβολισμό με τη μορφή Χ προς 1 αφαιρώντας 1 από τον παρονομαστή, ο οποίος είναι ο νικηφόρος γύρος του συνόλου. Βλέπε παραδείγματα πάνω από την παράγραφο.
Πιθανότητα των ζαριών
Τα ζάρια είναι ένα άλλο τυχερό παιχνίδι στο οποίο είναι σχετικά εύκολο να υπολογιστούν οι πιθανότητες. Πριν ξεκινήσουμε να υπολογίζουμε τις πιθανότητες να κερδίσετε στα ζάρια, ας ρίξουμε μια ματιά στην πιθανότητα των ζαριών.
Τα ζάρια έχουν 6 πλευρές. Η πιθανότητα να πέσει οποιοσδήποτε αριθμός είναι επομένως 1/6. Τα ζάρια παίζονται παραδοσιακά με δύο ζάρια. Οι πιθανότητες να συνδυαστούν δύο αριθμοί είναι επομένως 2/36. Ωστόσο, δεν μας ενδιαφέρουν τόσο οι συγκεκριμένοι αριθμοί όσο το άθροισμα αυτών των αριθμών, το οποίο είναι πολύ πιο σημαντικό στα ζάρια. Και πάλι, θα χρησιμοποιήσουμε τον τύπο: αριθμός νικηφόρων συνδυασμών/αριθμός όλων των συνδυασμών.
Ας πούμε ότι θέλουμε να μάθουμε την πιθανότητα για το άθροισμα 7. Κερδισμένοι συνδυασμοί: (1-6), (2-4), (3-3), (4-2), (6-1). Όπως μπορείτε να δείτε, υπάρχουν συνολικά 6 διαφορετικοί συνδυασμοί όπου το άθροισμα 7 μπορεί να κυλήσει σε δύο ζάρια. Και δεδομένου ότι ο αριθμός όλων των συνδυασμών είναι 36, η πιθανότητα του 7 είναι 6/36=0,1666.
Με αυτόν τον τρόπο, όλα τα άλλα πιθανά αποτελέσματα μπορούν εύκολα να υπολογιστούν.
|
Σύνολο |
Πιθανότητα |
|
2 |
1/36 |
|
3 |
2/36 |
|
4 |
3/36 |
|
5 |
4/36 |
|
6 |
5/36 |
|
7 |
6/36 |
|
8 |
5/36 |
|
9 |
4/36 |
|
10 |
3/36 |
|
11 |
2/36 |
|
12 |
1/36 |
Πιθανότητες νίκης στα ζάρια
Εν συντομία, ας ρίξουμε μια ματιά στους κανόνες για τα ζάρια. Το πιο συνηθισμένο στοίχημα είναι το Pass Line.
- Αν ρίξετε 7 ή 11, κερδίζετε.
- Αν ρίξετε 2, 3 ή 12, χάνετε.
- Σε άλλες περιπτώσεις (4, 5, 6, 8, 9 ή 10) καθορίζεται ένας πόντος και ρίχνεται μέχρι να ξαναριχτεί αυτός ο πόντος (νίκη) ή να πέσει 7 (ήττα).
Υπολογίζουμε πρώτα την πιθανότητα νίκης πριν καθορίσουμε το σημείο. Η πιθανότητα να πετύχεις το 7 είναι 6/36 και η πιθανότητα να πετύχεις το 11 είναι 2/36. Αυτά τα δύο κλάσματα πρέπει στη συνέχεια να προστεθούν για να προκύψει 3/36+2/36 = 2/9 = 0,2222.
Στρέφουμε τώρα την προσοχή μας στην περίπτωση που προσδιορίζεται ένα σημείο. Δηλαδή, όταν το σημείο είναι 4, 5, 6, 8, 9 ή 10. Ας ξεκινήσουμε με συνολικά 4.
Εάν ριχτεί 4, καθορίζεται ένας πόντος και ο παίκτης ρίχνει μέχρι να ριχτεί 4 ή 7. Εδώ εισερχόμαστε στη σφαίρα των υπό συνθήκη πιθανοτήτων. Αυτό μας λέει ποια είναι η πιθανότητα του γεγονότος Α αν το γεγονός Β συμβεί την ίδια στιγμή. Στην περίπτωσή μας, θα είναι ποια η πιθανότητα να κερδίσουμε (ρίχνει 4) αν ο γύρος τελειώσει (ρίχνει 4 ή 7). Στη συνέχεια εισάγουμε αυτές τις τιμές στον τύπο:
- P(A) = Falls άθροισμα του 4: 3/36
- P(A∩B) = μετά από προσαρμογές διαπιστώνουμε ότι είναι ίσο με A
- P(B) = Πτώσεις 4 ή 7: 3/36 + 6/36 = 9/36
Από αυτό προκύπτει ότι:
- P(4|4 ή 7) = (3/36)/(9/36) = 1/3
Με παρόμοιο τρόπο μπορούμε να υπολογίσουμε τα αθροίσματα των 5, 6, 8, 9 και 10.
- P(5|5 ή 7) = (4/36)/(10/36) = 2/5
- P(6|6 ή 7) = (5/36)/(11/36) = 5/11
- P(8|8 ή 7) = (5/36)/(11/36) = 5/11
- P(9|9 ή 7) = (4/36)/(10/36) = 2/5
- P(10|10 ή 7) = (3/36)/(9/36) = 1/3
Τώρα μπορούμε να υπολογίσουμε την πιθανότητα νίκης ως την πιθανότητα της αρχικής ρίψης όταν καθορίστηκε το σημείο και της επόμενης ρίψης όταν ο παίκτης κέρδισε.
- Αρχική ζαριά 4 x P(4|4 ή 7) = 3/36 x 1/3 = 1/36
- Αρχική ζαριά 5 x P(5|5 ή 7) = 4/36 x 2/5 = 2/45
- Αρχική ζαριά 6 x P(6|6 ή 7) = 5/36 x 5/11 = 25/396
- Αρχική ζαριά 8 x P(8|8 ή 7) = 5/36 x 5/11 = 25/396
- Αρχική ζαριά 9 x P(9|9 ή 7) = 4/36 x 2/5 = 2/45
- Αρχική ζαριά 10 x P(10|10 ή 7) = 3/36 x 1/3 = 1/36
Όλα αυτά τα κλάσματα μας δίνουν την πιθανότητα να κερδίσουμε αν η πρώτη ζαριά είναι 4, 5, 6, 8, 9 ή 10. Αν θέλετε να μάθετε τη συνολική πιθανότητα να κερδίσετε σε ένα στοίχημα Pass line, πρέπει να τα προσθέσετε όλα μαζί και να προσθέσετε την πιθανότητα να κερδίσετε πριν από το σημείο (ρίχνει 7 ή 11 - 2/9).
2/9 + 1/36 + 2/45 + 25/396 + 25/396 + 2/45 + 1/36 = 244/495
Επειδή 244/495 είναι ακριβώς 49,3%. Αυτό είναι λίγο κάτω από το 50%. Στην πραγματικότητα, πιθανώς δεν θα βρείτε καλύτερες πιθανότητες να κερδίσετε με μια πληρωμή 1 προς 1. Εκτός ίσως από το μπλάκτζακ, αν μπορείτε να μετρήσετε τα χαρτιά.
Πιθανότητα του Μπλάκτζακ
Το μπλάκτζακ είναι το παιχνίδι τύχης στο οποίο οι πιθανότητες έχουν τη μεγαλύτερη σημασία. Στο μπλάκτζακ, μπορείτε να επηρεάσετε το πλεονέκτημα του σπιτιού με τις ικανότητες και τις γνώσεις σας. Απλά πρέπει να γνωρίζετε τη βέλτιστη στρατηγική γι' αυτό, και αν ξέρετε πώς να μετράτε τα χαρτιά, θα παίξετε ακόμη και με το πλεονέκτημα του παίκτη. Στην πραγματικότητα δεν χρειάζεται να γνωρίζετε όλες τις συγκεκριμένες πιθανότητες, επειδή όλοι αυτοί οι υπολογισμοί έχουν ήδη γίνει από μαθηματικούς πριν από εσάς, οι οποίοι επινόησαν όλες τις τακτικές και στρατηγικές για το μπλάκτζακ.
Ωστόσο, για λόγους ενδιαφέροντος, θα δείξουμε πώς να υπολογίζουμε την πιθανότητα για ορισμένα σημαντικά φαινόμενα στο μπλάκτζακ.
Αν εξετάσουμε το πρόβλημα των πιθανοτήτων από τη σκοπιά μιας τράπουλας, είναι σαφές ότι ο αριθμός των πιθανών αποτελεσμάτων αυξάνεται ραγδαία. Το μπλάκτζακ παίζεται με μια τράπουλα 52 φύλλων, 4 χρωμάτων και 13 αξιών. Αυτό δίνει τις ακόλουθες αποδόσεις:
- Τραβάω έναν Άσσο από την τράπουλα (ή οποιοδήποτε μεμονωμένο φύλλο): 4/52=0,0769 (7,69%)
- Τραβάω μια πίκα από την τράπουλα: 13/52=0.25 (25%)
Ωστόσο, σε αντίθεση με την ρίψη κέρματος, τη ρουλέτα ή τους κουλοχέρηδες για παράδειγμα, μια τράπουλα έχει κάτι σαν "μνήμη". Ή μάλλον, αυτό σημαίνει ότι τα προηγούμενα αποτελέσματα επηρεάζουν τις τρέχουσες και μελλοντικές κινήσεις. Αυτό οφείλεται στο γεγονός ότι ένα φύλλο έχει πέσει από την τράπουλα και αυτό αλλάζει την αρχική κατάσταση. Ας δούμε ένα παράδειγμα όπου το πρώτο φύλλο που τραβήχτηκε από μια τράπουλα 52 φύλλων ήταν ένας άσος (7,69% πιθανότητα). Η πιθανότητα να τραβηχτεί ξανά ένας άσος ως δεύτερο φύλλο από την τράπουλα θα είναι τώρα διαφορετική. Μετά την πρώτη κλήρωση, ο αριθμός των άσων έχει μειωθεί σε 3 και ο αριθμός των φύλλων σε 51.
Πιθανότητα για blackjack φυσικό
Αυτό που ενδιαφέρει κάθε παίκτη είναι πρώτα η πιθανότητα του μπλάκτζακ. Δηλαδή, ποιες είναι οι πιθανότητες ένας παίκτης να πάρει έναν άσσο και ένα δεκάρι ακριβώς στην αρχή του γύρου - με άλλα λόγια, ένα φυσικό φύλλο.
Αυτή η κατάσταση μπορεί να συμβεί με δύο τρόπους και αν προσθέσουμε τους δύο τρόπους, θα έχουμε τις αποδόσεις μας στο μπλάκτζακ:
📌 Σημείωση: Μετράμε για μπλάκτζακ μονής τράπουλας. Οπότε 52 φύλλα, 4 άσσοι και 16 δεκάρια. Το φύλλο του ντίλερ δεν είναι ορατό, οπότε δεν επηρεάζει την πιθανότητα.
- Ο παίκτης λαμβάνει τον πρώτο άσο και ένα φύλλο δέκα.
Στον παίκτη μοιράζεται το πρώτο φύλλο άσου με πιθανότητα 4/52. Έτσι, ο παίκτης πρέπει να πάρει το δεύτερο φύλλο με ένα δεκάρι, και για αυτό οι πιθανότητες είναι 16/51. Αυτές οι δύο πιθανότητες πρέπει να πολλαπλασιαστούν μεταξύ τους για να προκύψει το 16/663.
- Ο παίκτης λαμβάνει το πρώτο δεκάρι και έναν άσσο.
Η πιθανότητα να λάβει ένας παίκτης το πρώτο φύλλο με αξία 10 είναι 16/52. Οι πιθανότητες ένας παίκτης να πάρει άσο μετά από αυτό είναι 4/51. Μετά τον πολλαπλασιασμό, έχουμε 16/663.
Αν θέλουμε να μάθουμε την πιθανότητα να πάρουμε μπλάκτζακ, απλά προσθέτουμε αυτά τα δύο φαινόμενα. Επομένως 16/663 + 16/663 = 32/663 = 4,827%. Με άλλα λόγια, ένας παίκτης παίρνει μπλάκτζακ περίπου μία φορά κάθε 20 χέρια. Μπορείτε να υπολογίσετε την πιθανότητα για τα τραπέζια πολλαπλών καταστρωμάτων με παρόμοιο τρόπο, κάτι που έχουμε ήδη κάνει για εσάς.
|
Αριθμός πακέτων |
Πιθανότητα |
|
1 |
4,827 % |
|
2 |
4,780 % |
|
3 |
4,764 % |
|
4 |
4,757 % |
|
5 |
4,752 % |
|
6 |
4,749 % |
Πιθανότητα αποτυχίας
Θα ήταν επίσης ενδιαφέρον να μάθετε ποιες είναι οι πιθανότητες να αποτύχετε. Και πάλι, θα επικεντρωθούμε σε ένα παράδειγμα όπου παίζετε μόνο με τον ντίλερ σε ένα τραπέζι με μία τράπουλα. Ας δούμε μια πολύ απλή κατάσταση όπου ένας παίκτης έχει 2 κάρτες με συνολική αξία 10, οπότε έχει 20 πόντους. Σε μια κατάσταση όπου ο παίκτης παίρνει ένα τρίτο φύλλο, έχουν ήδη παιχτεί 3 φύλλα από την τράπουλα. Αυτό αφήνει 49 κάρτες στην τράπουλα. Από αυτά τα 49 φύλλα, μόνο 4 άσσοι θα σας βοηθήσουν. Από αυτές τις 49, οι 45 κάρτες είναι ανεπιθύμητες. Επομένως, οι πιθανότητες να αποτύχει το παιχνίδι είναι 45/49=0,9183673.
Μπορείτε να υπολογίσετε άλλες πιθανότητες με παρόμοιο τρόπο. Πρέπει πάντα να είστε σε θέση να φαντάζεστε σωστά την κατάσταση. Αυτό είναι όλο.
|
Αξία του χεριού |
Πιθανότητα προτομών |
|
21 |
100 % |
|
20 |
92 % |
|
19 |
85 % |
|
18 |
77 % |
|
17 |
69 % |
|
16 |
62 % |
|
15 |
58 % |
|
14 |
56 % |
|
13 |
39 % |
|
12 |
31 % |
|
11 λιγότερα |
0 % |
Ας δούμε στη συνέχεια πόσο πιθανό είναι να σπάσει ο ντίλερ για κάθε φύλλο.
|
Αξία του χεριού |
Πιθανότητα προτομών |
|
2 |
35,30 % |
|
3 |
37,56 % |
|
4 |
40,28 % |
|
5 |
42,89 % |
|
6 |
42,08 % |
|
7 |
25,99 % |
|
8 |
23,86 % |
|
9 |
23,34 % |
|
10, J, Q, K |
21,43 % |
|
Ace |
11,65 % |
Πιθανότητα πόκερ
Το πόκερ είναι ένα άλλο παιχνίδι με χαρτιά όπου οι πιθανότητες είναι εξαιρετικά σημαντικές. Μεταξύ άλλων. Ας δούμε λοιπόν ποιες είναι οι πιθανότητές σας στο πόκερ.
Πιθανότητα προ-φλοπ
Τώρα που περιγράψαμε πώς λειτουργεί η πιθανότητα σε μια τράπουλα, ας περάσουμε στις πρακτικές εφαρμογές. Πρώτα απ' όλα, θα σας δείξουμε πώς να υπολογίσετε την πιθανότητα να ξεμείνετε από ζεύγη σε μια παρτίδα. (για παράδειγμα, το πολυσυζητημένο Aces). Σε αυτή την περίπτωση, πρέπει να πολλαπλασιάσουμε τις πιθανότητες μεταξύ τους.
(4/52) x (3/51) = (12/2652) = (1/221) = 0,004524 (0,45 %)
📌 Σημείωση: Εάν παίζετε πόκερ σε ένα καζίνο που μοιράζει περίπου 30 χέρια ανά ώρα, θα έχετε ένα ζευγάρι άσων περίπου μία φορά κάθε 7,5 ώρες παιχνιδιού.
Ποιες είναι λοιπόν οι πιθανότητες να πάρετε κάποιο από τα 13 πιθανά ζεύγη όταν μοιράζετε; Μπορούμε να υποθέσουμε ότι οι πιθανότητες είναι 1/221 ανά μεμονωμένο ζεύγος (βλ. παραπάνω τύπο). Μπορεί να υπάρχουν συνολικά 13 τέτοια ζεύγη, οπότε ο τύπος για τον υπολογισμό θα είναι 13/221=0,0588. Έτσι, μπορείτε να περιμένετε ένα ζευγάρι περίπου μία φορά κάθε 35 παιχνίδια.
Πιθανότητα στο πόκερ παίκτης εναντίον παίκτη
Ωστόσο, το πόκερ είναι ένα παιχνίδι για πολλούς παίκτες, που συνήθως παίζονται εναντίον άλλων. Ακολουθεί λοιπόν μια επιλογή από τις πιο συνηθισμένες καταστάσεις προ-φλοπ.
|
Το χέρι σας |
Χέρι του αντιπάλου σας |
Πιθανότητα νίκης |
|
Υψηλό ζεύγος |
Δύο χαμηλά φύλλα |
83 % |
|
Υψηλό ζεύγος |
Χαμηλό ζεύγος |
82 % |
|
Μέσο ζεύγος |
Υψηλή, χαμηλή κάρτα |
71 % |
|
Δύο υψηλά χαρτιά |
Δύο χαμηλά φύλλα |
63 % |
|
Δύο υψηλά χαρτιά |
Χαμηλό ζεύγος |
55 % |
Υπολογισμός της πιθανότητας με "outs"
Αν καταφέρετε να δείτε τα χαρτιά στο flop, σίγουρα θα σας ενδιαφέρει περισσότερο ποιες είναι οι πιθανότητες να βελτιώσετε το χέρι σας. Σε αυτή την περίπτωση, θα μιλήσουμε για τα λεγόμενα "outs". Στο πόκερ, ο όρος αυτός αναφέρεται σε κάθε φύλλο που μπορεί να σας βοηθήσει. Μια τέτοια συνηθισμένη περίπτωση μπορεί να είναι όταν ένας παίκτης έχει δύο φύλλα σε ένα χρώμα και δύο ακόμη φύλλα του ίδιου χρώματος εμφανίζονται στο flop. Ο παίκτης έχει τότε 4 φύλλα για να κάνει φλος και επομένως έχει 9 άουτ, αφήνοντας 9 φύλλα με τα οποία μπορεί να σχηματίσει φλος.
|
Αριθμός outs |
Flop - Turn |
Turn - River |
Γυρίστε ένα ποτάμι |
|
20 |
42,6 % |
43,5 % |
67,5 % |
|
19 |
40,4 % |
41,3 % |
65,0 % |
|
18 |
38,3 % |
39,1 % |
62,4 % |
|
17 |
36,2 % |
37,0 % |
59,8 % |
|
16 |
34,0 % |
34,8 % |
57,0 % |
|
15 |
31,9 % |
32,6 % |
54,1 % |
|
14 |
29,8 % |
30,4 % |
51,2 % |
|
13 |
27,7 % |
28,3 % |
48,1 % |
|
12 |
25,5 % |
26,1 % |
45,0 % |
|
11 |
23,4 % |
23,9 % |
41,7 % |
|
10 |
21,3 % |
21,7 % |
38,4 % |
|
9 |
19,1 % |
19,6 % |
35,0 % |
|
8 |
17,0 % |
17,4 % |
31,5 % |
|
7 |
14,9 % |
15,2 % |
27,8 % |
|
6 |
12,8 % |
13,0 % |
24,1 % |
|
5 |
10,6 % |
10,9 % |
20,3 % |
|
4 |
8,5 % |
8,7 % |
16,5 % |
|
3 |
6,4 % |
6,5 % |
12,5 % |
|
2 |
4,3 % |
4,3 % |
8,4 % |
|
1 |
2,1 % |
2,2 % |
4,3 % |
📌 Σημείωση: Υπάρχει μια πολύ εύκολη μέθοδος για τον υπολογισμό της πιθανότητας των outs, ώστε να μπορείτε να το κάνετε ακριβώς στο τραπέζι. Ονομάζεται γενικά κανόνας "τέσσερα και δύο". Μετά το flop, ο παίκτης απλά πολλαπλασιάζει τον αριθμό των outs επί 4 για να βρει την πιθανότητα για το turn και το river. Εάν δεν πάρει το φύλλο στο turn, απλά πολλαπλασιάζει τον αριθμό των outs επί δύο για να λάβει την κατά προσέγγιση πιθανότητα να πάρει το φύλλο στο river.
Και πάλι, μπορούμε να χρησιμοποιήσουμε το παράδειγμα ότι έχουμε 4 φύλλα του ίδιου χρώματος μετά το flop. Έτσι, τα outs σας είναι 9 φύλλα και η πιθανότητα φλος μετά το turn και το river είναι 36% (9x4). Ας υποθέσουμε ότι δεν παίρνετε κάρτα στη σειρά. Σε αυτή την περίπτωση, πολλαπλασιάζουμε τα outs επί δύο και βρίσκουμε ότι έχουμε 18% (9x2) πιθανότητα να μας τελειώσουν τα φύλλα του χρώματος στο river. Όπως μπορείτε να δείτε συγκρίνοντας τον πίνακα, αυτή η μέθοδος είναι πραγματικά απλή αλλά από την άλλη πλευρά ανακριβής, αλλά μπορεί να χρησιμοποιηθεί.

 GR
GR  English
English  čeština
čeština  Polski
Polski  Slovenčina
Slovenčina  Русский
Русский  Deutsch
Deutsch  Slovenski
Slovenski  Dutch
Dutch  Svenska
Svenska  Português
Português  Italiano
Italiano  Español
Español  Français
Français  Suomalainen
Suomalainen  Български
Български  Românesc
Românesc  Magyar
Magyar  Eesti
Eesti  Latviešu
Latviešu  Lietuvių
Lietuvių  やまと
やまと  中国
中国  Dansk
Dansk  Türkçe
Türkçe  ID
ID  Українська
Українська  한국어
한국어  Norsk
Norsk 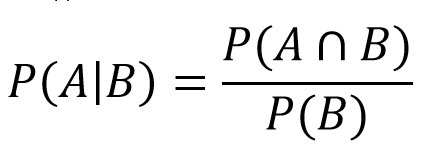


Πρέπει να είστε συνδεδεμένοι για να προσθέσετε ένα σχόλιο