Todennäköisyys ja kasinopelit
 Peter Sommer
Peter Sommer
Ymmärrätkö mahdollisuutesi? Jos aiot pelata kasinolla, sinun on varmistettava, että tunnet mahdollisuutesi ja ymmärrät ne täydellisesti. Miksi? Koska todennäköisyys on moottori, joka saa kasinot toimimaan. Ilman todennäköisyyttä uhkapeliala ei olisi mahdollinen.
Sattuma on yksinkertaisesti todennäköisyys sille, että jotain tapahtuu. Todennäköisyys on osa jokapäiväistä elämäämme. Kun päätämme ylittää vilkkaasti liikennöidyn kadun punaisia valoja päin, on olemassa tietty mahdollisuus, että jäämme auton alle, mutta vastapainoksi meillä on mahdollisuus ylittää katu nopeammin ja voittaa hieman aikaa.
Kun pelaamme uhkapeliä, arvioimme tietyn tapahtuman todennäköisyyden, jotta voimme muotoilla panoksemme. Näissä tapauksissa laskemme todennäköisyyden.
💡 Esimerkki todennäköisyydestä
Oletetaan, että meillä on pussi, jossa on neljä palloa, joista vain yksi on punainen ja kolme muuta sinistä. Todennäköisyys vetää esiin vain punainen pallo katsomatta on 1:4.
Todennäköisyys voidaan ilmaista monella eri tavalla. Voimme myös sanoa, että punaisen pallon todennäköisyys on 3:1, koska keskimäärin arvomme kolme sinistä palloa jokaista punaista palloa kohden.
Voimme ilmaista mahdollisuutemme myös prosentteina, joten todennäköisyytemme punaisen pallon vetämiseen on 25 %, jos pallon vetämisen todennäköisyys on 100 %. Joten 100 jaettuna neljällä saadaan 25 prosenttia.
Sinisen pallon vetämisen todennäköisyys on 75 %, jos on kolme sinistä palloa, joiden vetämisen todennäköisyys on 25 %.
Kasinopelien todennäköisyys
Kasino toimii sillä periaatteella, että se tarjoaa kertoimia, jotka eivät ole kovin hyviä pitkän aikavälin tuloksiimme nähden.
Esimerkki ilmapallopussista on yksinkertainen tapa osoittaa, miten kasino toimii. Sanotaan, että kasino tarjoaa 3:n kertoimen punaisen pallon arvonnalle. Jos panostat 5 dollaria, vedät sinisen pallon keskimäärin kolme kertaa neljässä yrityksessä ja häviät 15 dollaria, ja neljännellä kerralla vedät punaisen pallon ja voitat 10 dollaria, mutta kasino on silti 5 dollaria tappiolla.
Kaikessa uhkapelissä on kyse vain todennäköisyydestä. Kuka tahansa kokenut uhkapeluri voi kertoa sen sinulle. Siksi on tärkeää tuntea nämä numerot ja osata toimia niiden kanssa. Tässä näytämme nyt, miten todennäköisyys lasketaan uhkapeleissä. Jos ymmärrät periaatteen oikein, voit käyttää sitä minkä tahansa muun asian todennäköisyyden laskemiseen.
Todennäköisyys ruletissa
Ruletti on kuin onnenpyörä. Ja tiedätkö miksi? Selittämiseen tarvitaan vain kolme sanaa - Big Number Theory. Jokainen henkilö, joka pyörittää kasinoa tai tuottaa online-kasinopelejä, tuntee tämän teorian hyvin. Koska se on suoraan yhteydessä hänen ansioihinsa. Ja sen ansiosta kasino voittaa aina vedonlyöjät pitkällä aikavälillä. Kaikki liittyy todennäköisyyteen ja talon etuun.
📌 Huomautus: Kaikki artikkelin numerot viittaavat eurooppalaiseen rulettiin - laskemme siis 37 numeroa.
Miten todennäköisyys kirjoitetaan
Todennäköisyys voidaan kirjoittaa usealla eri tavalla. Tunnetuin niistä on luultavasti prosenttiosuudet. Näiden lisäksi käytetään murto- tai suhdelukuja.
- Ilmaistuna prosentteina (%) - tähän ei ole paljon lisättävää, mutta vain täydellisyyden vuoksi, tämä on valitun tapahtuman prosenttiosuus. Se lasketaan seuraavasti: (osa/kokonaismäärä)*100. Esimerkiksi todennäköisyys osua valittuun numeroon rulettipyörässä (suora): 1/37*100=2,7 %.
- Ilmaisu murtolukuja käyttäen (1/x) - Kun todennäköisyys ilmaistaan murtoluvulla, sanotaan, että ilmiö esiintyy 1 kerran X kokeesta. Numeerisessa lausekkeessa luotamme prosenttiosuuksien laskemiseen. Jos tarkastelemme edellä esitettyä esimerkkiä 1/37, tämä tarkoittaa, että tilastollisesti valittu numero rulettipyörässä putoaa yhden kerran 37 kierroksen aikana.
- Suhteellinen ilmaisu (x-1) - Joka kerta, kun X tapahtuu, valittu ilmiö tapahtuu 1 kertaa. Tässäkin tapauksessa pitäydymme ruletissa valitun numeron todennäköisyydessä. Tässä tapauksessa suhde kirjoitetaan 36:1. Tämä tarkoittaa sitä, että jokaisen 36 kierroksen jälkeen, jolloin numero ei putoa, tulee yksi kierros, jolloin valittu numero putoaa.
📌 Huomautus: Kuten suurten lukujen teoriassa sanotaan, todennäköisyys on pohjimmiltaan matemaattinen raja. Kun kokeiluja tehdään yhä enemmän, pääset realistisesti yhä lähemmäksi laskettua tulosta.
Kuten näet, murtolukuja ja suhdelukuja käyttävät lausekkeet ovat hyvin samankaltaisia. Ainoa ero on, että murtoluku laskee kaikki kierrokset, kun taas suhde jakaa kierrosten kokonaismäärän kahteen luokkaan.
Ruletin yksittäisten panosten todennäköisyystaulukko
|
Bet |
Ote lähteestä |
Suhde |
Prosenttiosuudet |
|
Suora veto |
1/2,055 |
1,055-1 |
48,6 % |
|
Pylväs |
1/3,08 |
2,08:1 |
32,4 % |
|
Tusina |
1/3,08 |
2,08:1 |
32,4 % |
|
Kuusi riviä |
1/6,17 |
5,17-1 |
16,2 % |
|
Corner |
1/9,25 |
8,25:1 |
10,8 % |
|
Street |
1/12,33 |
11,33-1 |
8,1 % |
|
Split |
1/19,5 |
18,5:1 |
5,4 % |
|
Suora |
1/37 |
36-1 |
2,7 % |
Suoran vedon todennäköisyys
Matemaattinen vertailu valitun ilmiön toistumisesta voisi myös olla mielenkiintoinen. Tässä tapauksessa olemme valinneet suoran vedon, eli esimerkiksi vedon punaiselle. Mikä on siis esimerkiksi 5 kertaa peräkkäin punaisen värin muuttumistodennäköisyys?
|
Kierrosten määrä |
Suhde |
Prosenttiosuudet |
|
1 |
1,06-1 |
48,6 % |
|
2 |
3,23:1 |
23,7 % |
|
3 |
7,69:1 |
11,5 % |
|
4 |
16,9:1 |
5,6 % |
|
5 |
35,7:1 |
2,73 % |
|
6 |
74,4:1 |
1,33 % |
|
7 |
154-1 |
0,65 % |
|
8 |
318-1 |
0,31 % |
|
9 |
654-1 |
0,15 % |
|
10 |
1 346-1 |
0,074 % |
|
15 |
49 423-1 |
0,002 % |
|
20 |
1 813 778-1 |
0,000055 % |
Kuten nähdään, ilmiön todennäköisyys pienenee nopeasti, kun spinnien määrä kasvaa. Muista kuitenkin, että nämä todennäköisyydet kuvaavat ilmiötä kokonaisuutena. Satunnaislukugeneraattori ei ota huomioon aiempia tuloksia, joten vaikka pelisarja, jossa punainen osuu 20 kertaa peräkkäin, tapahtuu kerran 1,813 miljoonassa pelissä, 21 pelikierroksella on sama talon etu ja todennäköisyys (eli 48,6 %) kuin kaikilla muillakin pelikierroksilla.
Usein tässä tapauksessa voidaan törmätä termiin Player's Fallacy (pelaajan harhaluulo), jossa vedonlyöjä uskoo, että jos yhteen väriin osuu useita kertoja peräkkäin, on suurempi todennäköisyys, että toiseen väriin osuu seuraavalla kierroksella. Todellisuudessa näin ei ole. Tunnetuin tapaus tästä harhaluulosta havaittiin vuonna 1913 Monte Carlon kasinolla, kun musta putosi rulettipyörässä 26 kertaa peräkkäin, ja melkein koko tämän uskomattoman putken ajan ja vielä sen jälkeenkin ihmiset panostivat hurjasti punaiseen. Silloin kasino tienasi mukavasti rahaa.
📌 Huomautus: Todennäköisyys, että väri osuu 26 kertaa peräkkäin, on 0,000000730870 %, ja se tapahtuu kerran 67 miljoonassa pelissä.
Miten laskea todennäköisyys ruletin
Haluatko tietää lisää yksittäisten vetojen kertoimia? Kokeile laskea ne itse. Prosenttiosuuksien ja todennäköisyyksien käyttäminen ei ole kovin monimutkaista. Yleisesti ottaen helpoin tapa on aloittaa murtoluvuista ja laskea niiden avulla edelleen prosentteja ja suhdelukuja. Jos esimerkiksi haluat laskea todennäköisyyden murtoluvulla tilanteessa, jossa punainen on punainen, toimitaan seuraavasti:
Punaisten kokonaismäärä pelikentällä / pelikenttien kokonaismäärä = 18/37.
Yhden kierroksen todennäköisyys
Tässäkin tapauksessa sovelletaan yksinkertaista sääntöä. Laske yksinkertaisesti voittoa tuottavien kenttien määrä ja jaa se kenttien kokonaismäärällä.
Esimerkiksi:
- Väri - 18/37
- Sudá/Lichá - 18/37
- Tusina - 12/37
- Numero 0 - 1/37
- Musta ja parillinen - 9/37 (pelikentässä on vain 9 numeroa, jotka ovat sekä mustia että parillisia).
- Tusina ja sarake - 4/37 (tusinassa ja sarakkeessa on vain 4 numeroa).
Aivan kuten voiton todennäköisyys, voit laskea myös häviämisen todennäköisyyden. Laske vain voittamattomien kenttien määrä ja jaa ne uudelleen kenttien kokonaismäärällä. Esimerkiksi todennäköisyys hävitä, jos panostat punaiselle, on 19/37 (18 mustaa kenttää + vihreä nolla).
📌 Huomautus: Jos haluat pienentää murtoluvun 1/x:ksi, jaa osoittaja ja nimittäjä yksinkertaisesti osoittajalla. Esimerkiksi 18/37 (jaat molemmat luvut 18:lla) on oikaisun jälkeen 1/2,055. Tämä tarkoittaa, että jokaista 2,055 kierrosta kohden yksi kierros on punainen tai musta.
Todennäköisyys moninkertaisille pyörähdyksille
Kun hallitset yksittäisten kierrosten laskennan, useiden kierrosten todennäköisyyden laskeminen on hyvin yksinkertaista. Kerro vain yksittäiset murtoluvut keskenään.
Esimerkkejä:
- spin - panos punaiselle = 18/37
- spin - panos per tusina = 12/37
Todennäköisyys voittaa molemmat kierrokset = (18/37)*(12/37)=1/6,34 eli 15,77 % eli 5,34:1.
- spin - suora veto - 1/37
- spin - suora veto - 1/37
Todennäköisyys voittaa molemmat kierrokset = (1/37)*(1*37)=1/1369 eli 0,073 % eli 1368:1.
- spin - panos mustalle ja parittomalle 9/37
- spin - panos parilliselle 18/37
- spin - sarakkeen veto 12/37
Todennäköisyys voittaa kaikki 3 kierrosta = (9/37)*(18/37)*(12/37)=1/26,06 eli 3,84 % eli 25,06:1.
Varsinainen muuntaminen merkintöjen välillä on jälleen hyvin helppoa. Prosenttiosuudet saadaan jakamalla murtoluku muodossa 1/x ja kertomalla se sitten sadalla. Suhteellinen merkintä saadaan muodossa X-1 vähentämällä nimittäjästä 1, joka on kokonaismäärän voittokierros. Katso esimerkit kappaleen yläpuolella.
Nopan todennäköisyys
Craps on toinen uhkapeli, jossa todennäköisyydet on suhteellisen helppo laskea. Ennen kuin alamme laskea noppapelien voittomahdollisuuksia, tarkastellaan nopanheiton todennäköisyyttä.
Nopassa on 6 sivua. Mahdollisuus, että jokin luku putoaa, on siis 1/6. Crapsia pelataan perinteisesti kahdella nopalla. Minkä tahansa kahden numeron yhdistymisen todennäköisyys on siis 2/36. Meitä eivät kuitenkaan kiinnosta niinkään yksittäiset numerot kuin niiden summa, joka on crapsissa paljon tärkeämpi. Jälleen kerran käytämme kaavaa: voittoyhdistelmien määrä/kaikkien yhdistelmien määrä.
Oletetaan, että haluamme tietää todennäköisyyden summalle 7. Voittavat yhdistelmät: (1-6), (2-4), (3-3), (4-2), (6-1). Kuten näet, on yhteensä 6 eri yhdistelmää, joissa kahdella nopalla voidaan heittää 7:n summa. Ja koska kaikkien yhdistelmien määrä on 36, todennäköisyys 7 on 6/36=0,1666.
Näin kaikki muut mahdolliset tulokset voidaan helposti laskea.
|
Yhteensä |
Todennäköisyys |
|
2 |
1/36 |
|
3 |
2/36 |
|
4 |
3/36 |
|
5 |
4/36 |
|
6 |
5/36 |
|
7 |
6/36 |
|
8 |
5/36 |
|
9 |
4/36 |
|
10 |
3/36 |
|
11 |
2/36 |
|
12 |
1/36 |
Kertoimet voittaa craps
Tarkastellaan lyhyesti noppasääntöjä. Yleisin veto on Pass Line.
- Jos heität 7 tai 11, voitat.
- Jos heität 2, 3 tai 12, häviät.
- Muissa tapauksissa (4, 5, 6, 8, 9 tai 10) määritetään piste ja heitetään, kunnes kyseinen piste heitetään uudelleen (voitto) tai heitetään 7 (häviö).
Laskemme ensin voiton todennäköisyyden ennen pisteen määrittämistä. Mahdollisuus osua 7:ään on 6/36 ja mahdollisuus osua 11:een on 2/36. Nämä kaksi murtolukua on sitten laskettava yhteen, jolloin saadaan 3/36+2/36 = 2/9 = 0,2222.
Seuraavaksi tarkastelemme tilannetta, jossa piste on määritetty. Eli kun piste on 4, 5, 6, 8, 9 tai 10. Aloitetaan yhteensä 4:llä.
Jos heitetään 4, piste määritetään, ja pelaaja heittää, kunnes heitetään 4 tai 7. Tässä päästään ehdollisen todennäköisyyden alueelle. Tämä kertoo, mikä on tapahtuman A todennäköisyys, jos tapahtuma B tapahtuu samaan aikaan. Meidän tapauksessamme se on se, mikä on todennäköisyys, että voitamme (heittää 4), jos kierros päättyy (heittää 4 tai 7). Tämän jälkeen nämä arvot liitetään kaavaan:
- P(A) = Falls 4:n summa: 3/36
- P(A∩B) = korjausten jälkeen havaitaan, että se on yhtä suuri kuin A.
- P(B) = putoaminen 4 tai 7: 3/36 + 6/36 = 9/36.
Tästä seuraa, että:
- P(4|4 tai 7) = (3/36)/(9/36) = 1/3.
Samalla tavalla voimme laskea 5, 6, 8, 9 ja 10 summat.
- P(5|5 tai 7) = (4/36)/(10/36) = 2/5.
- P(6|6 tai 7) = (5/36)/(11/36) = 5/11.
- P(8|8 tai 7) = (5/36)/(11/36) = 5/11.
- P(9|9 tai 7) = (4/36)/(10/36) = 2/5.
- P(10|10 tai 7) = (3/36)/(9/36) = 1/3.
Nyt voimme laskea voittomahdollisuuden alkuperäisen heiton todennäköisyytenä, kun piste määritettiin, ja seuraavan heiton todennäköisyytenä, kun pelaaja voitti.
- Alkuperäinen heitto 4 x P(4|4 tai 7) = 3/36 x 1/3 = 1/36.
- Alkuperäinen heitto 5 x P(5|5 tai 7) = 4/36 x 2/5 = 2/45.
- Alkuperäinen heitto 6 x P(6|6 tai 7) = 5/36 x 5/11 = 25/396.
- Alkuperäinen heitto 8 x P(8|8 tai 7) = 5/36 x 5/11 = 25/396.
- Alkuperäinen heitto 9 x P(9|9 tai 7) = 4/36 x 2/5 = 2/45.
- Alkuperäinen heitto 10 x P(10|10 tai 7) = 3/36 x 1/3 = 1/36.
Kaikki nämä murtoluvut antavat meille voiton todennäköisyyden, jos ensimmäinen heitto on 4, 5, 6, 8, 9 tai 10. Jos haluat tietää Pass line -vedon voittamisen kokonaistodennäköisyyden, sinun on laskettava ne kaikki yhteen ja lisättävä voittomahdollisuus ennen pistettä (heittää 7 tai 11 - 2/9).
2/9 + 1/36 + 2/45 + 25/396 + 25/396 + 2/45 + 1/36 = 244/495
Koska 244/495 on tasan 49,3 prosenttia. Se on hieman alle 50 prosenttia. Itse asiassa et luultavasti löydä parempaa voittomahdollisuutta 1:1-voitolla. Paitsi ehkä blackjack, jos osaat laskea kortteja.
Blackjackin todennäköisyys
Blackjack on uhkapeli, jossa todennäköisyydellä on eniten merkitystä. Blackjackissa voit vaikuttaa talon etuun taidoillasi ja tiedoillasi. Sinun on vain tiedettävä optimaalinen strategia tähän, ja jos osaat laskea kortteja, voit jopa pelata pelaajan eduksi. Sinun ei oikeastaan tarvitse tietää kaikkia erityisiä todennäköisyyksiä, koska kaikki nämä laskelmat ovat jo tehneet matemaatikot ennen sinua, jotka keksivät kaikki blackjackin taktiikat ja strategiat.
Kiinnostuksen vuoksi näytämme kuitenkin, miten blackjackin eräiden tärkeiden ilmiöiden todennäköisyys voidaan laskea.
Jos tarkastelemme todennäköisyysongelmaa korttipakan näkökulmasta, on selvää, että mahdollisten tulosten määrä kasvaa nopeasti. Blackjackia pelataan 52 kortin pakalla, jossa on 4 maata ja 13 arvoa. Näin saadaan seuraavat kertoimet:
- Nostan pakasta ässän (tai minkä tahansa yksittäisen kortin): 4/52=0.0769 (7.69%).
- Nostan pakasta pata: 13/52=0.25 (25%).
Toisin kuin esimerkiksi kolikonheitossa, ruletissa tai kolikkopeleissä, korttipakalla on kuitenkin jonkinlainen "muisti". Tai pikemminkin se tarkoittaa, että aiemmat tulokset vaikuttavat nykyisiin ja tuleviin liikkeisiin. Tämä johtuu siitä, että kortti on pudotettu pakasta, mikä muuttaa lähtötilannetta. Tarkastellaan esimerkkiä, jossa ensimmäinen 52 kortin pakasta nostettu kortti on ässä (7,69 % todennäköisyys). Todennäköisyys sille, että ässä arvotaan uudelleen pakan toisena korttina, on nyt erilainen. Ensimmäisen arvonnan jälkeen ässien määrä on laskenut kolmeen ja korttien määrä 51:een.
Todennäköisyys blackjack luonnollinen
Jokaista pelaajaa kiinnostaa ensin blackjackin todennäköisyys. Toisin sanoen, mitkä ovat mahdollisuudet, että pelaaja saa ässän ja kympin heti kierroksen alussa - toisin sanoen luonnollisen kortin.
Tämä tilanne voi tapahtua kahdella tavalla, ja jos laskemme nämä kaksi tapaa yhteen, saamme blackjackin kertoimen:
📌 Huomautus: Laskemme yhden pakan blackjackia. Eli 52 korttia, 4 ässää ja 16 kymppiä. Jakajan kortti ei näy, joten se ei vaikuta todennäköisyyteen.
- Pelaaja saa ensimmäisen ässän ja kymppikortin.
Pelaajalle jaetaan ensimmäinen ässäkortti todennäköisyydellä 4/52. Pelaajan on siis saatava toinen kortti, jossa on kymppi, ja sen todennäköisyys on 16/51. Nämä kaksi todennäköisyyttä on kerrottava keskenään, jotta saadaan 16/663.
- Pelaaja saa ensimmäisen kymmenen kortin ja ässän.
Todennäköisyys, että pelaaja saa ensimmäisen kortin, jonka arvo on 10, on 16/52. Todennäköisyys, että pelaaja saa ässän tämän jälkeen, on 4/51. Kertomisen jälkeen saadaan 16/663.
Jos haluamme tietää todennäköisyyden saada blackjack, laskemme vain nämä kaksi ilmiötä yhteen. Eli 16/663 + 16/663 = 32/663 = 4,827 %. Toisin sanoen pelaaja saa blackjackin noin kerran 20 käden välein. Voit laskea todennäköisyyden monipakkaisille pöydille samalla tavalla, minkä olemme jo tehneet puolestasi.
|
Pakkausten määrä |
Todennäköisyys |
|
1 |
4,827 % |
|
2 |
4,780 % |
|
3 |
4,764 % |
|
4 |
4,757 % |
|
5 |
4,752 % |
|
6 |
4,749 % |
Todennäköisyys epäonnistua
Saattaa myös olla mielenkiintoista tietää, mitkä ovat mahdollisuutesi epäonnistua. Keskitymme jälleen esimerkkitilanteeseen, jossa pelaat vain jakajan kanssa yhden pakan pöydässä. Tarkastellaan hyvin yksinkertaista tilannetta, jossa pelaajalla on kaksi korttia, joiden arvo on yhteensä 10, joten hänellä on 20 pistettä. Tilanteessa, jossa pelaaja saa kolmannen kortin, pakasta on jo pelattu kolme korttia. Näin pakkaan jää 49 korttia. Näistä 49 kortista vain 4 ässää auttaa sinua. Näistä 49 kortista 45 on ei-toivottuja. Näin ollen rysäyksen todennäköisyys on 45/49=0,9183673.
Voit laskea muut todennäköisyydet samalla tavalla. Sinun on aina pystyttävä kuvittelemaan tilanne oikein. Siinä kaikki.
|
Käden arvo |
Rikkojen todennäköisyys |
|
21 |
100 % |
|
20 |
92 % |
|
19 |
85 % |
|
18 |
77 % |
|
17 |
69 % |
|
16 |
62 % |
|
15 |
58 % |
|
14 |
56 % |
|
13 |
39 % |
|
12 |
31 % |
|
11 vähemmän |
0 % |
Seuraavaksi tarkastellaan, kuinka todennäköisesti jakaja menettää kortin kullakin kortilla.
|
Käden arvo |
Rikkojen todennäköisyys |
|
2 |
35,30 % |
|
3 |
37,56 % |
|
4 |
40,28 % |
|
5 |
42,89 % |
|
6 |
42,08 % |
|
7 |
25,99 % |
|
8 |
23,86 % |
|
9 |
23,34 % |
|
10, J, Q, K |
21,43 % |
|
Ace |
11,65 % |
Pokerin todennäköisyys
Pokeri on toinen korttipeli, jossa todennäköisyys on erittäin tärkeää. Muun muassa. Katsotaanpa siis, mitkä ovat mahdollisuutesi pokerissa.
Pre-flop-todennäköisyys
Nyt kun olemme hahmotelleet, miten todennäköisyys toimii korttipakassa, siirrymme käytännön sovelluksiin. Ensiksi näytämme, miten lasketaan todennäköisyys sille, että parit loppuvat kädestä. (esimerkiksi paljon puhuttu Ässät). Tässä tapauksessa meidän on kerrottava todennäköisyydet keskenään.
(4/52) x (3/51) = (12/2652) = (1/221) = 0,004524 (0,45 %)
📌 Huomautus: Jos pelaat pokeria kasinolla, joka jakaa noin 30 kättä tunnissa, saat ässäparin noin kerran 7,5 tunnin aikana.
Mitkä ovat siis mahdollisuudet saada jokin 13 mahdollisesta parista, kun jaat? Voimme olettaa, että todennäköisyys on 1/221 kutakin yksittäistä paria kohti (ks. edellä oleva kaava). Näitä pareja voi olla yhteensä 13, joten laskukaava on 13/221=0,0588. Voit siis odottaa paria noin kerran 35 pelissä.
Todennäköisyys pokerissa pelaaja vastaan pelaaja
Pokeri on kuitenkin moninpeli, jota pelataan yleensä toisiaan vastaan. Tässä on siis valikoima yleisimpiä pre-flop-tilanteita.
|
Sinun kätesi |
Vastustajan käsi |
Voiton todennäköisyys |
|
Korkea pari |
Kaksi matalaa korttia |
83 % |
|
Korkea pari |
Matala pari |
82 % |
|
Keskimmäinen pari |
Korkea, matala kortti |
71 % |
|
Kaksi korkeaa korttia |
Kaksi matalaa korttia |
63 % |
|
Kaksi korkeaa korttia |
Matala pari |
55 % |
Todennäköisyyden laskeminen "outs" -menetelmällä
Jos onnistut näkemään kortit flopilla, olet varmasti kiinnostunut siitä, mitkä ovat mahdollisuutesi parantaa kättäsi. Tässä tapauksessa puhumme niin sanotuista "outs". Pokerissa tämä termi viittaa kaikkiin kortteihin, jotka voivat auttaa sinua. Tällainen yleinen tapaus voi olla, kun pelaajalla on kaksi korttia samaa maata ja flopissa on kaksi muuta samaa maata olevaa korttia. Pelaajalla on tällöin 4 korttia värin muodostamiseen, joten hänellä on 9 korttia pois, jolloin hänellä on 9 korttia, joilla hän voi muodostaa värin.
|
Ulostulojen määrä |
Floppi - Turn |
Turn - River |
Käännä joki |
|
20 |
42,6 % |
43,5 % |
67,5 % |
|
19 |
40,4 % |
41,3 % |
65,0 % |
|
18 |
38,3 % |
39,1 % |
62,4 % |
|
17 |
36,2 % |
37,0 % |
59,8 % |
|
16 |
34,0 % |
34,8 % |
57,0 % |
|
15 |
31,9 % |
32,6 % |
54,1 % |
|
14 |
29,8 % |
30,4 % |
51,2 % |
|
13 |
27,7 % |
28,3 % |
48,1 % |
|
12 |
25,5 % |
26,1 % |
45,0 % |
|
11 |
23,4 % |
23,9 % |
41,7 % |
|
10 |
21,3 % |
21,7 % |
38,4 % |
|
9 |
19,1 % |
19,6 % |
35,0 % |
|
8 |
17,0 % |
17,4 % |
31,5 % |
|
7 |
14,9 % |
15,2 % |
27,8 % |
|
6 |
12,8 % |
13,0 % |
24,1 % |
|
5 |
10,6 % |
10,9 % |
20,3 % |
|
4 |
8,5 % |
8,7 % |
16,5 % |
|
3 |
6,4 % |
6,5 % |
12,5 % |
|
2 |
4,3 % |
4,3 % |
8,4 % |
|
1 |
2,1 % |
2,2 % |
4,3 % |
📌 Huomaa: On olemassa erittäin helppo menetelmä outien todennäköisyyden laskemiseen, joten voit tehdä sen suoraan pöydässä. Sitä kutsutaan yleisesti "neljä ja kaksi" -säännöksi. Flopin jälkeen pelaaja yksinkertaisesti kertoo outien määrän neljällä saadakseen turnin ja riverin todennäköisyyden. Jos hän ei saa korttia turnilla, hän yksinkertaisesti kertoo outien määrän kahdella saadakseen likimääräisen todennäköisyyden saada kortti riverillä.
Voimme jälleen käyttää esimerkkiä, jossa flopin jälkeen sinulla on 4 samaa maata olevaa korttia. Ulostulosi ovat siis 9 korttia, ja värin todennäköisyys turnin ja riverin jälkeen on 36 % (9x4). Oletetaan, että et saa korttia vuorollasi. Tässä tapauksessa kerromme outit kahdella ja saamme selville, että meillä on 18 prosentin (9x2) mahdollisuus, että kortit loppuvat riverillä. Kuten taulukkoa vertailemalla voitte nähdä, tämä menetelmä on todella yksinkertainen mutta toisaalta epätarkka, mutta sitä voidaan käyttää.

 FI
FI  English
English  čeština
čeština  Polski
Polski  Slovenčina
Slovenčina  Русский
Русский  Deutsch
Deutsch  Slovenski
Slovenski  Dutch
Dutch  Svenska
Svenska  Português
Português  Italiano
Italiano  Español
Español  Français
Français  Български
Български  Românesc
Românesc  Magyar
Magyar  Eesti
Eesti  Ελληνική
Ελληνική  Latviešu
Latviešu  Lietuvių
Lietuvių  やまと
やまと  中国
中国  Dansk
Dansk  Türkçe
Türkçe  ID
ID  Українська
Українська  한국어
한국어  Norsk
Norsk 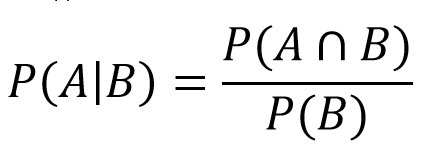


Sinun on oltava kirjautuneena sisään , jotta voit lisätä kommentin