Probabilitatea și jocurile de cazino
 Peter Sommer
Peter Sommer
Îți înțelegi șansele? Dacă aveți de gând să jucați la un cazinou, trebuie să vă asigurați că vă cunoașteți șansele și că le înțelegeți perfect. De ce? Pentru că probabilitatea este motorul care face ca cazinourile să funcționeze. Fără probabilitate, industria jocurilor de noroc nu ar fi posibilă.
Șansa este pur și simplu probabilitatea ca ceva să se întâmple. Probabilitatea face parte din viața noastră de zi cu zi. Atunci când decidem să traversăm o stradă aglomerată la culoarea roșie a semaforului, există o anumită șansă de a fi loviți de o mașină, dar în schimb avem șansa de a traversa strada mai repede și de a câștiga ceva timp liber.
Atunci când jucăm, estimăm probabilitatea ca un anumit eveniment să se întâmple pentru a ne formula pariul. În aceste cazuri se calculează probabilitatea.
💡 Exemplu de probabilitate
Să spunem că avem un sac care conține patru bile, dintre care doar una este roșie, iar celelalte trei sunt albastre. Probabilitatea de a extrage doar bila roșie fără să se uite este de 1 la 4.
Există mai multe moduri de a exprima probabilitatea. Putem spune, de asemenea, că există o șansă de 3 la 1 împotriva roșului, deoarece, în medie, extragem trei bile albastre pentru fiecare bilă roșie extrasă.
De asemenea, ne putem exprima șansele sub formă de procente, astfel încât probabilitatea de a extrage o bilă roșie este de 25% dacă există o șansă de 100% de a extrage o bilă. Deci, 100 împărțit la patru ne dă 25%.
Probabilitatea de a extrage o bilă albastră este de 75% dacă există trei bile albastre cu o șansă de 25% de extragere.
Probabilitatea jocurilor de cazino
Cazinoul funcționează pe principiul de a oferi cote care nu sunt atât de bune având în vedere rezultatul nostru pe termen lung.
Exemplul unui sac de baloane este un mod simplu de a arăta cum funcționează un cazinou. Să presupunem că un cazinou oferă o cotă de 3 la extragerea unei bile roșii. Dacă pariați 5 dolari, atunci, în medie, în patru încercări veți trage bila albastră de 3 ori și veți pierde 15 dolari, iar a patra oară veți trage bila roșie și veți câștiga 10 dolari, dar cazinoul va fi în continuare pe minus cu 5 dolari.
Toate jocurile de noroc se bazează doar pe probabilitate. Orice jucător cu experiență
vă va spune asta. Prin urmare, este esențial să cunoașteți aceste numere și să știți cum să lucrați cu ele. Așadar, vă vom arăta acum cum să calculați probabilitatea în jocurile de noroc. Dacă înțelegeți corect principiul, îl puteți folosi pentru a calcula probabilitatea oricărui alt lucru.
Probabilitatea la ruletă
Ruleta este ca Roata Norocului. Și știi de ce? Este nevoie doar de 3 cuvinte pentru a explica - Teoria numerelor mari. Fiecare persoană care conduce un cazinou sau produce jocuri de cazinou online cunoaște foarte bine această teorie. Pentru că este direct legată de veniturile sale. Și datorită acestui fapt, cazinoul câștigă întotdeauna în fața pariorilor pe termen lung. Totul este legat de probabilitate și de avantajul casei.
📌 Notă: Toate numerele din articol se referă la Ruleta Europeană - deci numărăm 37 de numere.
Cum se scrie probabilitatea
Există mai multe moduri de a scrie probabilitatea. Probabil că cel mai cunoscut este procentul. Pe lângă acestea, se folosesc și expresii care utilizează o fracție sau un raport.
- Exprimat ca procent (%) - nu sunt multe de adăugat aici, dar, pentru a fi complet, acesta este procentul pentru evenimentul selectat. Se calculează ca (parte/total)*100. De exemplu, probabilitatea de a nimeri numărul selectat pe o roată de ruletă (Straight): 1/37*100=2,7%.
- Exprimarea cu ajutorul fracțiilor (1/x) - Atunci când exprimăm probabilitatea cu ajutorul unei fracții, spunem că fenomenul se produce de 1 dată din X încercări. În exprimarea numerică, ne bazăm pe calcularea procentelor. Dacă luăm în considerare exemplul 1/37 de mai sus, aceasta înseamnă că un număr selectat statistic pe roata ruletei va cădea de 1 dată în 37 de rotiri.
- Exprimare prin raport (x la 1) - De fiecare dată când se produce X, fenomenul selectat se produce de 1 dată. Și aici rămânem la probabilitatea pentru numărul selectat la ruletă. În acest caz, raportul va fi scris ca fiind de 36 la 1. Acest lucru înseamnă că, după fiecare 36 de învârtiri în care numărul nu cade, va exista un caz în care numărul selectat va cădea.
📌 Notă: Așa cum spune teoria numerelor mari, probabilitatea este în esență o limită matematică. Cu din ce în ce mai multe încercări, vă apropiați în mod realist de rezultatul calculat.
După cum puteți vedea, expresiile care utilizează fracții și cele care utilizează rapoarte sunt foarte asemănătoare. Singura diferență este că o fracțiune numără toate rotirile, în timp ce un raport împarte numărul total de rotiri în două categorii.
Tabelul de probabilități pentru pariurile individuale la ruletă
|
Pariu |
Extras din |
Raport |
Procentaje |
|
Un pariu straight |
1/2,055 |
1,055 la 1 |
48,6 % |
|
Coloana |
1/3,08 |
2.08 la 1 |
32,4 % |
|
Duzina |
1/3,08 |
2.08 la 1 |
32,4 % |
|
Șase linii |
1/6,17 |
5.17 la 1 |
16,2 % |
|
Colțar |
1/9,25 |
8.25 la 1 |
10,8 % |
|
Strada |
1/12,33 |
11.33 la 1 |
8,1 % |
|
Split |
1/19,5 |
18,5 la 1 |
5,4 % |
|
Drept |
1/37 |
36 la 1 |
2,7 % |
Probabilitatea pentru un pariu straight
O comparație matematică pentru repetarea fenomenului selectat ar putea fi, de asemenea, interesantă. În acest caz am ales un pariu direct, de exemplu, un pariu pe roșu. Deci, care va fi probabilitatea de schimbare a roșului de 5 ori la rând, de exemplu?
|
Numărul de învârtiri |
Raport |
Procentaje |
|
1 |
1.06 la 1 |
48,6 % |
|
2 |
3.23 la 1 |
23,7 % |
|
3 |
7.69 la 1 |
11,5 % |
|
4 |
16,9 la 1 |
5,6 % |
|
5 |
35,7 la 1 |
2,73 % |
|
6 |
74,4 la 1 |
1,33 % |
|
7 |
154 la 1 |
0,65 % |
|
8 |
318 la 1 |
0,31 % |
|
9 |
654 la 1 |
0,15 % |
|
10 |
1 346 la 1 |
0,074 % |
|
15 |
49 423 la 1 |
0,002 % |
|
20 |
1 813 778 la 1 |
0,000055 % |
După cum se poate observa, pe măsură ce numărul de rotiri crește, probabilitatea acestui fenomen scade rapid. Cu toate acestea, nu uitați că aceste probabilități descriu fenomenul în ansamblu. Generatorul de numere aleatoare nu ia în considerare rezultatele anterioare, astfel încât, chiar dacă o serie de jocuri în care roșul lovește de 20 de ori la rând apare o dată la 1,813 milioane de jocuri, o rundă de 21 de jocuri va avea același avantaj și aceeași probabilitate (adică 48,6%) ca orice altă rundă de jocuri.
Adesea, în acest caz, se întâlnește termenul de Player's Fallacy, în care pariorul crede că, dacă o culoare este lovită de mai multe ori la rând, există o probabilitate mai mare ca cealaltă culoare să fie lovită la următoarea rotire. În realitate, nu este cazul. Cel mai faimos caz al acestei erori a fost observat în 1913 la cazinoul din Monte Carlo, când negrul a căzut de 26 de ori la rând pe roata de ruletă, iar pe aproape întreaga durată a acestei serii incredibile și chiar și după ce s-a încheiat, oamenii au pariat frenetic pe roșu. Atunci, cazinoul a făcut niște bani foarte frumoși.
📌 Notă: Probabilitatea ca o culoare să fie lovită de 26 de ori la rând este de 0,000000730870% și apare o dată la 67 de milioane de jocuri.
Cum se calculează probabilitatea de ruleta
Doriți să aflați mai multe cote pentru pariurile individuale? Încercați să le calculați singur. Lucrul cu procentele și probabilitățile nu este foarte complicat. În general, cel mai simplu este să începeți cu fracții și să le folosiți pentru a calcula procentele și ratele ulterioare. De exemplu, dacă doriți să calculați probabilitatea într-o fracție pentru o situație în care roșul este roșu, faceți următoarele:
Numărul total de roșii de pe terenul de joc/Numărul total de terenuri de joc = 18/37
Probabilitatea pentru o rotație
Din nou, aici se aplică o regulă simplă. Calculați pur și simplu numărul de câmpuri care vă vor aduce un câștig și împărțiți-l la numărul total de câmpuri.
De exemplu:
- Culoare - 18/37
- Sudá/Lichá - 18/37
- Duzină - 12/37
- Numărul 0 - 1/37
- Negru și par - 9/37 (există doar 9 numere pe terenul de joc care sunt atât negre cât și pare)
- Zeci și coloană - 4/37 (există doar 4 numere într-o duzină și într-o coloană)
La fel ca și probabilitatea de a câștiga, puteți calcula probabilitatea de a pierde. Numărați doar numărul de terenuri care nu au câștigat și împărțiți-le din nou la numărul total de terenuri. De exemplu, probabilitatea de a pierde dacă pariați pe roșu este de 19/37 (18 câmpuri negre + zero verde).
📌 Notă: Pentru a reduce o fracție la 1/x, împărțiți pur și simplu numărătorul și numitorul la numitor. De exemplu, 18/37 (împărțiți ambele numere la 18) va fi 1/2,055 după ajustare. Aceasta înseamnă că, la fiecare 2,055 ture, o tură va avea ca rezultat un roșu sau un negru.
Probabilitatea pentru rotiri multiple
Odată ce ați stăpânit calculul pentru o singură învârtire, calcularea probabilității pentru mai multe învârtiri este foarte simplă. Trebuie doar să înmulțiți fracțiile individuale una cu cealaltă.
Exemple:
- spin - pariu pe roșu = 18/37
- rotire - pariu pe duzină = 12/37
Probabilitatea de a câștiga ambele runde = (18/37)*(12/37)=1/6,34 sau 15,77% sau 5,34 la 1
- spin - pariu direct - 1/37
- spin - pariu direct - 1/37
Probabilitatea de a câștiga ambele runde = (1/37)*(1*37)=1/1369 sau 0.073% sau 1368 la 1
- spin - pariu pe negru și impar 9/37
- spin - pariați pe par 18/37
- rotire - pariu pe coloană 12/37
Probabilitatea de a câștiga toate cele 3 runde = (9/37)*(18/37)*(12/37)=1/26,06 sau 3,84% sau 25,06 la 1.
Conversia efectivă între intrări este, din nou, foarte ușoară. Procentele se obțin prin împărțirea fracției sub forma 1/x și apoi prin înmulțirea cu 100. Notația proporțională se obține sub forma X la 1 prin scăderea lui 1 din numitor, care este runda câștigătoare din total. A se vedea exemplele de mai sus.
Probabilitatea de zaruri
Craps este un alt joc de noroc în care este relativ ușor de calculat șansele. Înainte de a trece la calcularea șanselor de câștig la zaruri, să aruncăm o privire la probabilitatea de aruncare a zarurilor în sine.
Zarurile au 6 fețe. Șansa ca orice număr să cadă este, prin urmare, 1/6. Craps se joacă în mod tradițional cu două zaruri. Șansele ca oricare două numere să se combine sunt, prin urmare, de 2/36. Cu toate acestea, nu ne interesează atât de mult numerele specifice, cât suma acestor numere, care este mult mai importantă la zaruri. Din nou, vom folosi formula: numărul de combinații câștigătoare/numărul tuturor combinațiilor.
Să spunem că vrem să știm probabilitatea pentru suma 7. Combinații câștigătoare: (1-6), (2-4), (3-3), (4-2), (6-1). După cum puteți vedea, există un total de 6 combinații diferite în care suma de 7 poate fi aruncată pe două zaruri. Și cum numărul tuturor combinațiilor este 36, probabilitatea de 7 este 6/36=0.1666.
În acest fel, toate celelalte rezultate posibile pot fi calculate cu ușurință.
|
Total |
Probabilitate |
|
2 |
1/36 |
|
3 |
2/36 |
|
4 |
3/36 |
|
5 |
4/36 |
|
6 |
5/36 |
|
7 |
6/36 |
|
8 |
5/36 |
|
9 |
4/36 |
|
10 |
3/36 |
|
11 |
2/36 |
|
12 |
1/36 |
Șanse de câștig la craps
Pe scurt, să aruncăm o privire la regulile de joc cu zaruri. Cel mai comun pariu este Pass Line.
- Dacă scoți un 7 sau un 11, câștigi.
- Dacă obțineți un 2, 3 sau 12, pierdeți.
- În alte cazuri (4, 5, 6, 8, 9 sau 10) se determină un punct și se aruncă până când acel punct este aruncat din nou (câștig) sau până când se aruncă un 7 (pierdere).
Mai întâi calculăm probabilitatea de câștig înainte de a determina punctul. Șansa de a nimeri 7 este de 6/36, iar șansa de a nimeri 11 este de 2/36. Aceste două fracții trebuie apoi adunate pentru a obține 3/36+2/36 = 2/9 = 0,2222.
Ne îndreptăm acum atenția spre situația în care se determină un punct. Adică, atunci când punctul este 4, 5, 6, 8, 9 sau 10. Să începem cu un total de 4.
Dacă iese un 4, se stabilește un punct și jucătorul aruncă până când iese un 4 sau un 7. Aici intrăm pe tărâmul probabilității condiționate. Aceasta ne spune care este probabilitatea ca evenimentul A să aibă loc în același timp cu evenimentul B. În cazul nostru, aceasta va fi probabilitatea de a câștiga (aruncă un 4) dacă runda se termină (aruncă un 4 sau un 7). Apoi introducem aceste valori în formulă:
- P(A) = Sumă de 4 căderi: 3/36
- P(A∩B) = după ajustări constatăm că este egal cu A
- P(B) = Căderi 4 sau 7: 3/36 + 6/36 = 9/36
Rezultă că:
- P(4|4 sau 7) = (3/36)/(9/36) = 1/3
În mod similar, putem calcula sumele 5, 6, 8, 9 și 10
- P(5|5 sau 7) = (4/36)/(10/36) = 2/5
- P(6|6 sau 7) = (5/36)/(11/36) = 5/11
- P(8|8 sau 7) = (5/36)/(11/36) = 5/11
- P(9|9 sau 7) = (4/36)/(10/36) = 2/5
- P(10|10 sau 7) = (3/36)/(9/36) = 1/3
Acum putem calcula șansa de a câștiga ca fiind probabilitatea de aruncare inițială a cărții, atunci când a fost determinat punctul, și următoarea aruncare a cărții, atunci când jucătorul a câștigat.
- Rulajul original 4 x P(4|4 sau 7) = 3/36 x 1/3 = 1/36
- Rularea inițială 5 x P(5|5 sau 7) = 4/36 x 2/5 = 2/45
- Aruncarea inițială 6 x P(6|6 sau 7) = 5/36 x 5/11 = 25/396
- Rulajul original 8 x P(8|8 sau 7) = 5/36 x 5/11 = 25/396
- Rularea originală 9 x P(9|9 sau 7) = 4/36 x 2/5 = 2/45
- Rulajul original 10 x P(10|10 sau 7) = 3/36 x 1/3 = 1/36
Toate aceste fracții ne dau probabilitatea de a câștiga dacă prima aruncare este 4, 5, 6, 8, 9 sau 10. Dacă doriți să aflați probabilitatea totală de câștig la un pariu pe linia Pass, trebuie să le adunați pe toate și să adăugați șansa de câștig înainte de punct (aruncă un 7 sau un 11 - 2/9).
2/9 + 1/36 + 2/45 + 25/396 + 25/396 + 2/45 + 1/36 = 244/495
Pentru că 244/495 este exact 49,3%. Asta înseamnă puțin sub 50%. De fapt, probabil că nu veți găsi o șansă mai bună de câștig cu un câștig 1 la 1. Poate cu excepția blackjack-ului, dacă știi să numeri cărțile.
Probabilitatea de Blackjack
Blackjack este un joc de noroc în care șansele contează cel mai mult. La blackjack, puteți influența avantajul casei prin abilitățile și cunoștințele dumneavoastră. Trebuie doar să știi care este strategia optimă în acest sens, iar dacă știi cum să numeri cărțile, vei juca chiar cu avantajul jucătorului. De fapt, nu este nevoie să cunoști toate probabilitățile specifice, deoarece toate aceste calcule au fost deja făcute de matematicieni înaintea ta, care au venit cu toate tacticile și strategiile pentru blackjack.
Cu toate acestea, de dragul interesului, vom arăta cum să calculăm probabilitatea pentru unele fenomene importante din blackjack.
Dacă privim problema probabilității din perspectiva unui pachet de cărți, este clar că numărul de rezultate posibile crește rapid. Blackjack se joacă cu un pachet de 52 de cărți, 4 culori și 13 valori. Acest lucru dă următoarele cote:
- Extrag un As din pachet (sau orice carte individuală): 4/52=0.0769 (7.69%)
- Extrag o pică din pachet: 13/52=0.25 (25%)
Cu toate acestea, spre deosebire de aruncarea unei monede, de ruletă sau de aparatele de joc, de exemplu, un pachet de cărți are un fel de "memorie". Sau, mai degrabă, înseamnă că rezultatele anterioare au un efect asupra mișcărilor actuale și viitoare. Acest lucru se datorează faptului că o carte a fost aruncată din pachet, ceea ce schimbă situația de start. Să analizăm un exemplu în care prima carte extrasă dintr-un pachet de 52 de cărți a fost un As (7,69% șanse). Probabilitatea ca un As să fie extras din nou ca a doua carte din pachet va fi diferită. După prima extragere, numărul de ași a scăzut la 3, iar numărul de cărți la 51.
Probabilitatea pentru blackjack natural
Ceea ce interesează mai întâi pe fiecare jucător este probabilitatea de blackjack. Adică, care sunt șansele ca un jucător să primească un as și un zece chiar la începutul rundei - cu alte cuvinte, o carte naturală.
Această situație se poate întâmpla în două moduri, iar dacă adunăm cele două moduri, obținem șansele noastre la blackjack:
📌 Notă: Numărăm pentru blackjack cu un singur pachet. Așadar, 52 de cărți, 4 ași și 16 zeci. Cartea dealerului nu este vizibilă, deci nu va afecta probabilitatea.
- Jucătorul primește primul as și o carte de zece.
Jucătorul primește prima carte As cu o probabilitate de 4/52. Așadar, jucătorul trebuie să obțină a doua carte cu un zece, iar pentru aceasta șansele sunt de 16/51. Aceste două probabilități trebuie înmulțite între ele pentru a obține 16/663.
- Jucătorul primește prima carte de zece și un as.
Probabilitatea ca un jucător să primească prima carte cu valoarea 10 este de 16/52. Șansele ca un jucător să primească un As după aceea sunt de 4/51. După înmulțire, obținem 16/663.
Dacă dorim să aflăm probabilitatea de a obține un blackjack, trebuie doar să adunăm aceste două fenomene. Deci 16/663 + 16/663 = 32/663 = 4,827%. Cu alte cuvinte, un jucător primește un blackjack cam o dată la 20 de mâini. Puteți calcula probabilitatea pentru mesele cu mai multe pachete într-un mod similar, ceea ce am făcut deja pentru dumneavoastră.
|
Număr de pachete |
Probabilitate |
|
1 |
4,827 % |
|
2 |
4,780 % |
|
3 |
4,764 % |
|
4 |
4,757 % |
|
5 |
4,752 % |
|
6 |
4,749 % |
Probabilitatea de a fi arestat
De asemenea, ar putea fi interesant de știut care sunt șansele tale de a fi arestat. Din nou, ne vom concentra pe un exemplu de situație în care joci doar cu dealerul la o masă cu un singur pachet. Să ne uităm la o situație foarte simplă în care un jucător are 2 cărți cu o valoare totală de 10, deci are 20 de puncte. În situația în care jucătorul primește o a treia carte, au fost deja jucate 3 cărți din pachet. Rămân astfel 49 de cărți în pachet. Dintre aceste 49 de cărți, doar 4 ași vă vor ajuta. Dintre acestea 49, 45 de cărți sunt nedorite. Prin urmare, șansele de a fi arestat sunt 45/49=0,9183673.
Puteți calcula alte probabilități într-un mod similar. Întotdeauna trebuie să vă puteți imagina corect situația. Asta e tot.
|
Valoarea mâinii |
Probabilitatea de a se produce o explozie |
|
21 |
100 % |
|
20 |
92 % |
|
19 |
85 % |
|
18 |
77 % |
|
17 |
69 % |
|
16 |
62 % |
|
15 |
58 % |
|
14 |
56 % |
|
13 |
39 % |
|
12 |
31 % |
|
11 mai puțin |
0 % |
În continuare, să vedem care este probabilitatea ca dealerul să fie eliminat pentru fiecare carte.
|
Valoarea mâinii |
Probabilitatea de a se produce o explozie |
|
2 |
35,30 % |
|
3 |
37,56 % |
|
4 |
40,28 % |
|
5 |
42,89 % |
|
6 |
42,08 % |
|
7 |
25,99 % |
|
8 |
23,86 % |
|
9 |
23,34 % |
|
10, J, Q, K |
21,43 % |
|
Ace |
11,65 % |
Probabilitatea de poker
Pokerul este un alt joc de cărți în care probabilitatea este extrem de importantă. Printre altele. Așadar, hai să vedem care sunt șansele tale la poker.
Probabilitatea pre-flop
Acum că am prezentat modul în care funcționează probabilitatea într-un pachet de cărți, să trecem la aplicațiile practice. În primul rând, vom arăta cum să calculăm probabilitatea de a rămâne fără perechi într-o mână. (de exemplu, mult discutatul Aces). În acest caz, trebuie să înmulțim probabilitățile una cu cealaltă.
(4/52) x (3/51) = (12/2652) = (1/221) = 0,004524 (0,45 %)
📌 Notă: Dacă joci poker într-un cazinou care împarte aproximativ 30 de mâini pe oră, vei primi o pereche de ași cam o dată la fiecare 7 ore și jumătate de joc.
Deci, care sunt șansele de a obține una dintre cele 13 perechi posibile atunci când dai cărțile? Putem presupune că șansele sunt de 1/221 pentru fiecare pereche în parte (a se vedea formula de mai sus). Pot exista 13 perechi în total, astfel încât formula de calcul va fi 13/221=0,0588. Așadar, vă puteți aștepta la o pereche cam o dată la 35 de meciuri.
Probabilitatea în poker jucător contra jucător
Cu toate acestea, pokerul este un joc multiplayer, jucat de obicei unul împotriva celuilalt. Iată o selecție a celor mai frecvente situații pre-flop.
Mâna ta
|
Mâna adversarului tău |
Probabilitatea de câștig |
|
|
Perechea mare |
Două cărți mici |
83 % |
|
Perechea mare |
Pereche scăzută |
82 % |
|
Perechea de mijloc |
Carte mare, carte mică |
71 % |
|
Două cărți mari |
Două cărți mici |
63 % |
|
Două cărți mari |
Pereche scăzută |
55 % |
Calcularea probabilității prin "outs"
Dacă reușiți să vedeți cărțile de pe flop, veți fi cu siguranță mai interesat de șansele pe care le aveți de a vă îmbunătăți mâna. În acest caz, vom vorbi despre așa-numitele "outs". În poker, acest termen se referă la orice carte care te poate ajuta. Un astfel de caz comun poate fi atunci când un jucător deține două cărți de aceeași culoare și alte două cărți de aceeași culoare apar pe flop. Jucătorul are apoi 4 cărți pentru culoare și are astfel 9 out-uri, rămânând 9 cărți cu care poate forma o culoare.
|
Număr de ieșiri |
Flop - Turn |
Turn - River |
Întoarce un râu |
|
20 |
42,6 % |
43,5 % |
67,5 % |
|
19 |
40,4 % |
41,3 % |
65,0 % |
|
18 |
38,3 % |
39,1 % |
62,4 % |
|
17 |
36,2 % |
37,0 % |
59,8 % |
|
16 |
34,0 % |
34,8 % |
57,0 % |
|
15 |
31,9 % |
32,6 % |
54,1 % |
|
14 |
29,8 % |
30,4 % |
51,2 % |
|
13 |
27,7 % |
28,3 % |
48,1 % |
|
12 |
25,5 % |
26,1 % |
45,0 % |
|
11 |
23,4 % |
23,9 % |
41,7 % |
|
10 |
21,3 % |
21,7 % |
38,4 % |
|
9 |
19,1 % |
19,6 % |
35,0 % |
|
8 |
17,0 % |
17,4 % |
31,5 % |
|
7 |
14,9 % |
15,2 % |
27,8 % |
|
6 |
12,8 % |
13,0 % |
24,1 % |
|
5 |
10,6 % |
10,9 % |
20,3 % |
|
4 |
8,5 % |
8,7 % |
16,5 % |
|
3 |
6,4 % |
6,5 % |
12,5 % |
|
2 |
4,3 % |
4,3 % |
8,4 % |
|
1 |
2,1 % |
2,2 % |
4,3 % |
📌 Notă: Există o metodă foarte simplă de calculare a probabilității de outs, astfel încât să o puteți face chiar la masă. În general, aceasta se numește regula "patru și doi". După flop, jucătorul înmulțește pur și simplu numărul de outs cu 4 pentru a afla probabilitatea pentru turn și river. Dacă nu primește cartea la turn, înmulțește pur și simplu numărul de outs cu doi pentru a obține probabilitatea aproximativă de a primi cartea la river.
Din nou, putem folosi exemplul de a avea 4 cărți de aceeași culoare după flop. Deci, out-urile tale sunt 9 cărți, iar probabilitatea de a avea culoare după turn și river este de 36% (9x4). Să spunem că nu primești o carte la rândul tău. În acest caz, înmulțim cu doi outs și aflăm că avem o șansă de 18% (9x2) de a rămâne fără cărți de aceeași culoare pe river. După cum puteți vedea prin compararea tabelului, această metodă este foarte simplă, dar pe de altă parte inexactă, dar poate fi utilizată.

 RO
RO  English
English  čeština
čeština  Polski
Polski  Slovenčina
Slovenčina  Русский
Русский  Deutsch
Deutsch  Slovenski
Slovenski  Dutch
Dutch  Svenska
Svenska  Português
Português  Italiano
Italiano  Español
Español  Français
Français  Suomalainen
Suomalainen  Български
Български  Magyar
Magyar  Eesti
Eesti  Ελληνική
Ελληνική  Latviešu
Latviešu  Lietuvių
Lietuvių  やまと
やまと  中国
中国  Dansk
Dansk  Türkçe
Türkçe  ID
ID  Українська
Українська  한국어
한국어  Norsk
Norsk 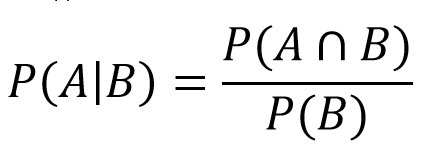


Trebuie să fii logat pentru a adăuga un comentariu