Sandsynlighed og casinospil
 Peter Sommer
Peter Sommer
Er du klar over dine chancer? Hvis du skal spille på et casino, skal du sikre dig, at du kender dine chancer og forstår dem perfekt. Hvorfor? Fordi sandsynlighed er den motor, der får casinoer til at fungere. Uden sandsynlighed ville spilleindustrien ikke være mulig uden sandsynlighed.
Tilfældighed er simpelthen sandsynligheden for, at noget vil ske. Sandsynlighed er en del af vores hverdag. Når vi beslutter os for at krydse en travl gade ved rødt lys, er der en vis chance for at blive ramt af en bil, men til gengæld har vi mulighed for at krydse gaden hurtigere og vinde lidt tid til overs.
Når vi spiller, vurderer vi sandsynligheden for, at en bestemt hændelse vil ske, for at kunne formulere vores indsats. Det er i disse tilfælde, at vi beregner sandsynligheden.
💡 Eksempel på sandsynlighed
Lad os sige, at vi har en pose med fire kugler, hvoraf kun én er rød og de tre andre er blå. Sandsynligheden for at trække bare den røde kugle ud uden at kigge er 1 ud af 4.
Der er flere måder at udtrykke sandsynlighed på. Vi kan også sige, at der er en chance på 3 til 1 mod rødt, fordi vi i gennemsnit trækker tre blå kugler for hver rød kugle, der trækkes.
Vi kan også udtrykke vores chancer som en procentdel, så vores sandsynlighed for at trække en rød kugle er 25 %, hvis der er 100 % chance for at trække en kugle. 100 divideret med fire giver altså 25 %.
Sandsynligheden for at trække en blå kugle er 75 %, hvis der er tre blå kugler med en chance på 25 % for at trække en blå kugle.
Sandsynlighed for casinospil
Casinoet opererer efter princippet om at tilbyde odds, der ikke er så gode i forhold til vores langsigtede resultat.
Eksemplet med en pose balloner er en enkel måde at vise, hvordan et kasino fungerer. Lad os sige, at et casino tilbyder odds 3 for at trække en rød kugle. Hvis du satser 5 $, vil du i gennemsnit i fire forsøg trække din blå kugle tre gange og tabe 15 $, og fjerde gang vil du trække din røde kugle og vinde 10 $, men casinoet vil stadig være i underskud med 5 $.
Alle spil handler kun om sandsynlighed. Det kan enhver erfaren spiller fortælle dig. Det er derfor vigtigt at kende disse tal og vide, hvordan man skal arbejde med dem. Så her vil vi nu vise dig, hvordan du beregner sandsynligheden i spil. Hvis du forstår princippet korrekt, kan du bruge det til at beregne sandsynligheden for hvad som helst andet.
Sandsynlighed ved roulette
Roulette er som lykkehjulet. Og ved du hvorfor? Det kræver kun 3 ord at forklare det - Big Number Theory. Enhver person, der driver et casino eller producerer online casinospil, kender denne teori udmærket. Fordi den er direkte forbundet med hans indtjening. Og takket være det vinder casinoet altid over spillerne i det lange løb. Alt er forbundet med sandsynlighed og husets fordel.
📌 Bemærk: Alle numre i artiklen henviser til europæisk roulette - så vi tæller 37 numre.
Hvordan man skriver sandsynlighed
Der er flere måder at skrive sandsynlighed på. Den mest kendte er nok procenter. Derudover anvendes udtryk, der anvender brøk- eller forholdstal.
- Udtrykt som en procentdel (%) - der er ikke meget at tilføje her, men for fuldstændighedens skyld er dette procentdelen for den valgte begivenhed. Den beregnes som (del/samlet)*100. For eksempel sandsynligheden for at ramme det valgte nummer på et roulettehjul (Straight): 1/37*100=2,7%.
- Udtryk ved hjælp af brøker (1/x) - Når man udtrykker sandsynligheden ved hjælp af en brøk, siger man, at fænomenet forekommer 1 gang ud af X forsøg. I det numeriske udtryk er vi afhængige af at beregne procenter. Hvis vi ser på 1/37-eksemplet ovenfor, betyder det, at et statistisk udvalgt nummer på rouletten vil falde 1 gang i 37 omgange.
- Udtryk i forhold (x til 1) - Hver gang X forekommer, forekommer det valgte fænomen 1 gang. Her holder vi os igen til sandsynligheden for det valgte nummer ved roulette. I dette tilfælde vil forholdet blive skrevet som 36 til 1. Det betyder, at efter hver 36 spins, hvor tallet ikke falder, vil der være et tilfælde, hvor det valgte tal falder.
📌 Bemærk: Som det fremgår af teorien om store tal, er sandsynlighed i bund og grund en matematisk grænse. Med flere og flere forsøg kommer du realistisk set tættere og tættere på det beregnede resultat.
Som du kan se, er udtrykkene med brøker og med forholdstal meget ens. Den eneste forskel er, at en brøk tæller alle spins, mens et forhold opdeler de samlede spins i to kategorier.
Tabel over sandsynligheder for individuelle indsatser i roulette
|
Spil |
Uddrag af |
Forhold |
Procentdele |
|
Et straight bet |
1/2,055 |
1,055 til 1 |
48,6 % |
|
Kolonne |
1/3,08 |
2,08 til 1 |
32,4 % |
|
Dusinet |
1/3,08 |
2,08 til 1 |
32,4 % |
|
Seks linjer |
1/6,17 |
5,17 til 1 |
16,2 % |
|
Hjørne |
1/9,25 |
8,25 til 1 |
10,8 % |
|
Gade |
1/12,33 |
11,33 til 1 |
8,1 % |
|
Split |
1/19,5 |
18,5 til 1 |
5,4 % |
|
Lige |
1/37 |
36 til 1 |
2,7 % |
Sandsynlighed for et straight-spil
Det kunne også være interessant at foretage en matematisk sammenligning af gentagelsen af det udvalgte fænomen. I dette tilfælde har vi valgt en straight bet, f.eks. en indsats på rødt. Så hvad vil den ændrede sandsynlighed for rødt være 5 gange i træk, for eksempel?
|
Antal spins |
Forhold |
Procentdele |
|
1 |
1,06 til 1 |
48,6 % |
|
2 |
3,23 til 1 |
23,7 % |
|
3 |
7,69 til 1 |
11,5 % |
|
4 |
16,9 til 1 |
5,6 % |
|
5 |
35,7 til 1 |
2,73 % |
|
6 |
74,4 til 1 |
1,33 % |
|
7 |
154 til 1 |
0,65 % |
|
8 |
318 til 1 |
0,31 % |
|
9 |
654 til 1 |
0,15 % |
|
10 |
1 346 til 1 |
0,074 % |
|
15 |
49 423 til 1 |
0,002 % |
|
20 |
1 813 778 til 1 |
0,000055 % |
Som det fremgår, falder sandsynligheden for dette fænomen hurtigt, efterhånden som antallet af spins stiger. Husk dog på, at disse sandsynligheder beskriver fænomenet som helhed. Generatoren af tilfældige tal tager ikke hensyn til tidligere resultater, så selv om en spil-serie, hvor rød rammer 20 gange i træk, forekommer én gang for hver 1,813 millioner spil, vil en runde med 21 spil have den samme huskant og sandsynlighed (dvs. 48,6 %) som alle andre spillerunder.
I dette tilfælde kan man ofte støde på udtrykket Player's Fallacy, hvor spilleren tror, at hvis en farve rammes flere gange i træk, er der større sandsynlighed for, at den anden farve rammes i det næste spin. I virkeligheden er dette ikke tilfældet. Det mest berømte tilfælde af denne fejlslutning blev observeret i 1913 på Monte Carlo Casino, da sort faldt 26 gange i træk på roulettehjulet, og i næsten hele denne utrolige periode, og selv efter at den var slut, satsede folk frenetisk på rødt. Det var dengang, kasinoet tjente nogle rigtig gode penge.
📌 Bemærk: Sandsynligheden for, at en farve rammes 26 gange i træk, er 0,000000730870% og forekommer én gang i 67 millioner spil.
Hvordan man beregner sandsynligheden for roulette
Vil du vide flere odds for individuelle spil? Prøv selv at beregne dem. Det er ikke særlig kompliceret at arbejde med procenter og sandsynligheder. Generelt er det lettest at starte med brøker og bruge dem til at beregne yderligere procenter og forholdstal. Hvis du f.eks. ønsker at beregne sandsynligheden i en brøk for en situation, hvor den røde er rød, gør du følgende:
Samlet antal røde på spillepladsen/Total antal spillepladser = 18/37
Sandsynlighed for et spin
Igen gælder en simpel regel her. Du skal blot beregne det antal felter, der giver dig en gevinst, og dividere det med det samlede antal felter.
For eksempel:
- Farve - 18/37
- Sudá/Lichá - 18/37
- Dusin - 12/37
- Nummer 0 - 1/37
- Sort og lige - 9/37 (der er kun 9 numre i spillefeltet, som både er sorte og lige)
- Dusin og kolonne - 4/37 (der er kun 4 tal i et dusin og i en kolonne)
Ligesom sandsynligheden for at vinde kan du også beregne sandsynligheden for at tabe. Du skal blot tælle antallet af felter, der ikke har vundet, og dividere dem igen med det samlede antal felter. For eksempel er sandsynligheden for at tabe, hvis du satser på rødt, 19/37 (18 sorte felter + grønt nul).
📌 Bemærk: For at reducere en brøk til 1/x skal du blot dividere tælleren og nævneren med tælleren. F.eks. vil 18/37 (du dividerer begge tal med 18) være 1/2,055 efter justeringen. Det betyder, at for hver 2,055 omgange vil en omgang resultere i en rød eller en sort.
Sandsynlighed for flere spins
Når du først har lært at beregne sandsynligheden for enkelte spins, er det meget nemt at beregne sandsynligheden for flere spins. Du skal blot gange de enkelte brøker med hinanden.
Eksempler:
- spin - indsats på rød = 18/37
- spin - indsats pr. dusin = 12/37
Sandsynligheden for at vinde begge runder = (18/37)*(12/37)=1/6,34 eller 15,77% eller 5,34 til 1
- spin - straight bet - 1/37
- spin - straight bet - 1/37
Sandsynligheden for at vinde begge runder = (1/37)*(1*37)=1/1369 eller 0,073% eller 1368 til 1
- spin - spil på sort og ulige 9/37
- spin - spil på lige 18/37
- spin - kolonneindsats 12/37
Sandsynligheden for at vinde alle 3 runder = (9/37)*(18/37)*(12/37)=1/26,06 eller 3,84% eller 25,06 til 1
Selve konverteringen mellem posterne er igen meget let. Du får procenterne ved at dividere brøken i form af 1/x og derefter gange med 100. Du får den proportionale notation i form af X til 1 ved at trække 1 fra nævneren, som er den vindende runde af totalen. Se eksempler over dette afsnit.
Sandsynlighed for terninger
Craps er et andet hasardspil, hvor det er relativt nemt at beregne oddsene. Før vi går i gang med at beregne oddsene for at vinde ved craps, skal vi se på sandsynligheden for selve terningekastene.
Terningerne har 6 sider. Chancen for, at et tal falder, er derfor 1/6. Craps spilles traditionelt med to terninger. Oddset for at to tal kombineres er derfor 2/36. Vi er dog ikke så meget interesseret i de specifikke tal som i summen af disse tal, hvilket er meget vigtigere i craps. Igen bruger vi formlen: antal vindende kombinationer/antal af alle kombinationer.
Lad os sige, at vi ønsker at kende sandsynligheden for summen 7. Vinderkombinationer: (1-6), (2-4), (3-3), (4-2), (6-1). Som du kan se, er der i alt 6 forskellige kombinationer, hvor summen 7 kan kastes på to terninger. Og da antallet af alle kombinationer er 36, er sandsynligheden for 7 6/36=0,1666
På denne måde kan alle andre mulige resultater let beregnes.
|
I alt |
Sandsynlighed |
|
2 |
1/36 |
|
3 |
2/36 |
|
4 |
3/36 |
|
5 |
4/36 |
|
6 |
5/36 |
|
7 |
6/36 |
|
8 |
5/36 |
|
9 |
4/36 |
|
10 |
3/36 |
|
11 |
2/36 |
|
12 |
1/36 |
Odds for at vinde ved craps
Lad os kort se på terningsreglerne. Den mest almindelige indsats er Pass Line.
- Hvis du får 7 eller 11, vinder du
- Hvis du kaster 2, 3 eller 12, taber du.
- I andre tilfælde (4, 5, 6, 8, 9 eller 10) bestemmes et point og kastes indtil dette point kastes igen (gevinst) eller der kastes et 7-tal (tab).
Vi beregner først sandsynligheden for at vinde, før vi bestemmer pointet. Chancen for at ramme 7 er 6/36 og chancen for at ramme 11 er 2/36. Disse to brøker skal så lægges sammen og giver 3/36+2/36 = 2/9 = 0,2222.
Vi vender nu vores opmærksomhed mod den situation, hvor et punkt er bestemt. Det vil sige, når punktet er 4, 5, 6, 8, 9 eller 10. Lad os starte med i alt 4.
Hvis der kastes en 4, fastsættes et point, og spilleren kaster, indtil der kastes en 4 eller en 7. Det er her, vi kommer ind på området for betinget sandsynlighed. Dette fortæller os, hvad sandsynligheden for hændelse A er, hvis hændelse B indtræffer på samme tidspunkt. I vores tilfælde vil det være sandsynligheden for, at vi vinder (kastede en 4'er), hvis runden slutter (kastede en 4'er eller en 7'er). Vi indsætter derefter disse værdier i formlen:
- P(A) = Falls summen af 4: 3/36
- P(A∩B) = efter justeringer finder vi, at den er lig med A
- P(B) = fald 4 eller 7: 3/36 + 6/36 = 9/36
Det følger heraf:
- P(4|4 eller 7) = (3/36)/(9/36) = 1/3
På samme måde kan vi beregne summen af 5, 6, 8, 9 og 10
- P(5|5 eller 7) = (4/36)/(10/36) = 2/5
- P(6|6 eller 7) = (5/36)/(11/36) = 5/11
- P(8|8 eller 7) = (5/36)/(11/36) = 5/11
- P(9|9 eller 7) = (4/36)/(10/36) = 2/5
- P(10|10 eller 7) = (3/36)/(9/36) = 1/3
Nu kan vi beregne chancen for at vinde som sandsynligheden for det oprindelige kast, hvor pointet blev bestemt, og det næste kast, hvor spilleren vandt.
- Oprindeligt kast 4 x P(4|4 eller 7) = 3/36 x 1/3 = 1/36
- Oprindeligt kast 5 x P(5|5 eller 7) = 4/36 x 2/5 = 2/45
- Oprindeligt kast 6 x P(6|6 eller 7) = 5/36 x 5/11 = 25/396
- Oprindeligt kast 8 x P(8|8 eller 7) = 5/36 x 5/11 = 25/396
- Oprindeligt kast 9 x P(9|9 eller 7) = 4/36 x 2/5 = 2/45
- Oprindeligt kast 10 x P(10|10 eller 7) = 3/36 x 1/3 = 1/36
Alle disse brøker giver os sandsynligheden for at vinde, hvis det første kast er 4, 5, 6, 8, 9 eller 10. Hvis du vil kende den samlede sandsynlighed for at vinde på en Pass line-indsats, skal du lægge dem alle sammen sammen og tilføje chancen for at vinde før pointet (7 eller 11 - 2/9).
2/9 + 1/36 + 2/45 + 25/396 + 25/396 + 2/45 + 1/36 = 244/495
Fordi 244/495 er præcis 49,3 %. Det er lige under 50 %. Faktisk vil du sandsynligvis ikke finde en bedre chance for at vinde med en 1:1 udbetaling. Bortset fra måske blackjack, hvis du kan tælle kort.
Sandsynlighed for Blackjack
Blackjack er det spil, hvor oddsene betyder mest. I blackjack kan du påvirke husets fordel med dine evner og din viden. Du skal bare kende den optimale strategi for dette, og hvis du ved, hvordan man tæller kort, vil du endda spille med spillerens fordel. Du behøver faktisk ikke at kende alle de specifikke sandsynligheder, for alle disse beregninger er allerede blevet udført af matematikere før dig, som fandt på alle taktikker og strategier til blackjack.
Af hensyn til interessen vil vi dog vise, hvordan man kan beregne sandsynligheden for nogle vigtige fænomener i blackjack.
Hvis vi ser på sandsynlighedsproblemet ud fra et kortspil, er det klart, at antallet af mulige udfald stiger hurtigt. Blackjack spilles med et sæt på 52 kort, 4 farver og 13 værdier. Dette giver følgende odds:
- Jeg trækker et es fra bunken (eller et individuelt kort): 4/52=0,0769 (7,69 %)
- Jeg trækker en spar fra bunken: 13/52=0,25 (25%)
Men i modsætning til f.eks. møntkast, roulette eller spilleautomater har et kortspil noget af en "hukommelse". Eller rettere sagt, det betyder, at tidligere resultater har en indvirkning på nuværende og fremtidige træk. Dette skyldes, at et kort er blevet tabt fra bunken, og det ændrer startsituationen. Lad os se på et eksempel, hvor det første kort, der trækkes fra et spil med 52 kort, er et es (7,69 % chance). Sandsynligheden for, at et es vil blive trukket igen som det andet kort fra bunken, vil nu være anderledes. Efter den første trækning er antallet af esser faldet til 3 og antallet af kort til 51.
Sandsynlighed for blackjack natural
Det, som alle spillere først vil være interesseret i, er sandsynligheden for blackjack. Det vil sige, hvad er chancerne for, at en spiller får et es og et ti-kort lige i starten af runden - med andre ord, en natural.
Denne situation kan opstå på to måder, og hvis vi lægger de to måder sammen, får vi vores odds på blackjack:
📌 Bemærk: Vi tæller for single deck blackjack. Altså 52 kort, 4 esser og 16 tiere. Dealerens kort er ikke synligt, så det påvirker ikke sandsynligheden.
- Spilleren får det første es og et ti-kort
Spilleren får det første es-kort med 4/52 sandsynlighed. Spilleren skal altså få det andet kort med en tier, og for det er odds 16/51. Disse to sandsynligheder skal ganges med hinanden for at få 16/663.
- Spilleren får det første ti-kort og et es
Sandsynligheden for, at en spiller får det første kort med værdien 10, er 16/52. Oddsene for at en spiller får et es efter dette er 4/51. Efter multiplikation får vi 16/663.
Hvis vi ønsker at kende sandsynligheden for at få blackjack, skal vi blot lægge disse to fænomener sammen. Så 16/663 + 16/663 = 32/663 = 4,827%. Med andre ord får en spiller en blackjack ca. én gang hver 20. hånd. Du kan beregne sandsynligheden for borde med flere dæk på en lignende måde, hvilket vi allerede har gjort for dig.
|
Antal pakker |
Sandsynlighed |
|
1 |
4,827 % |
|
2 |
4,780 % |
|
3 |
4,764 % |
|
4 |
4,757 % |
|
5 |
4,752 % |
|
6 |
4,749 % |
Sandsynlighed for at gå fallit
Det kan også være interessant at vide, hvad dine chancer for at blive bust er. Igen vil vi fokusere på en situation, hvor du kun spiller med dealeren ved et single deck-bord. Lad os tage et kig på en meget simpel situation, hvor en spiller har 2 kort med en værdi på 10 i alt, så han har 20 point. I en situation, hvor spilleren får et tredje kort, er der allerede blevet spillet 3 kort fra bunken. Dermed er der 49 kort tilbage i bunken. Ud af disse 49 kort er det kun 4 esser, der kan hjælpe dig. Af disse 49 er 45 kort uønskede. Derfor er oddsene for en bust 45/49=0,9183673.
Du kan beregne andre sandsynligheder på samme måde. Man skal altid være i stand til at forestille sig situationen korrekt. Det er det hele.
|
Værdi af hånden |
Sandsynlighed for busts |
|
21 |
100 % |
|
20 |
92 % |
|
19 |
85 % |
|
18 |
77 % |
|
17 |
69 % |
|
16 |
62 % |
|
15 |
58 % |
|
14 |
56 % |
|
13 |
39 % |
|
12 |
31 % |
|
11 mindre |
0 % |
Lad os nu se på, hvor sandsynligt det er, at dealeren vil gå bust for hvert kort.
|
Værdi af hånden |
Sandsynlighed for busts |
|
2 |
35,30 % |
|
3 |
37,56 % |
|
4 |
40,28 % |
|
5 |
42,89 % |
|
6 |
42,08 % |
|
7 |
25,99 % |
|
8 |
23,86 % |
|
9 |
23,34 % |
|
10, J, Q, K |
21,43 % |
|
Ace |
11,65 % |
Sandsynlighed for poker
Poker er et andet kortspil, hvor sandsynligheden er ekstremt vigtig. Blandt andet. Så lad os se på, hvordan dine chancer er i poker.
Sandsynlighed før flop
Nu hvor vi har skitseret, hvordan sandsynligheden fungerer i et spil kort, kan vi gå over til praktiske anvendelser. Først og fremmest vil vi vise, hvordan du beregner sandsynligheden for at løbe tør for par i en hånd. (f.eks. de meget omtalte Aces). I dette tilfælde skal vi gange sandsynlighederne med hinanden.
(4/52) x (3/51) = (12/2652) = (1/221) = 0,004524 (0,45 %)
📌 Bemærk: Hvis du spiller poker på et kasino, der giver ca. 30 hænder i timen, vil du få et par esser ca. en gang hver 7,5 times spil.
Så hvad er chancerne for at få et af de 13 mulige par, når du giver? Vi kan antage, at oddsene er 1/221 pr. individuelt par (se ovenstående formel). Der kan være 13 af disse par i alt, så formlen for beregningen bliver 13/221=0,0588. Så du kan forvente et par ca. en gang hver 35. kamp.
Sandsynlighed i poker spiller mod spiller
Poker er dog et spil for flere spillere, som normalt spilles mod hinanden. Så her er et udvalg af de mest almindelige pre-flop-situationer.
|
Din hånd |
Din modstanders hånd |
Sandsynlighed for at vinde |
|
Højt par |
To lave kort |
83 % |
|
Højt par |
Lavt par |
82 % |
|
Mellemste par |
Højt, lavt kort |
71 % |
|
To høje kort |
To lave kort |
63 % |
|
To høje kort |
Lavt par |
55 % |
Beregning af sandsynlighed ved hjælp af "outs"
Hvis det lykkes dig at se kortene på floppet, vil du helt sikkert være yderligere interesseret i, hvad dine chancer er for at forbedre din hånd. I dette tilfælde vil vi tale om de såkaldte "outs". I poker henviser dette udtryk til alle kort, der kan hjælpe dig. Et sådant almindeligt tilfælde kan være, når en spiller har to kort i en farve, og to andre kort i samme farve dukker op på floppet. Spilleren har derefter 4 kort til flush og har således 9 outs, hvilket efterlader 9 kort til at danne en flush med.
|
Antal outs |
Flop - Turn |
Turn - River |
Drej en flod |
|
20 |
42,6 % |
43,5 % |
67,5 % |
|
19 |
40,4 % |
41,3 % |
65,0 % |
|
18 |
38,3 % |
39,1 % |
62,4 % |
|
17 |
36,2 % |
37,0 % |
59,8 % |
|
16 |
34,0 % |
34,8 % |
57,0 % |
|
15 |
31,9 % |
32,6 % |
54,1 % |
|
14 |
29,8 % |
30,4 % |
51,2 % |
|
13 |
27,7 % |
28,3 % |
48,1 % |
|
12 |
25,5 % |
26,1 % |
45,0 % |
|
11 |
23,4 % |
23,9 % |
41,7 % |
|
10 |
21,3 % |
21,7 % |
38,4 % |
|
9 |
19,1 % |
19,6 % |
35,0 % |
|
8 |
17,0 % |
17,4 % |
31,5 % |
|
7 |
14,9 % |
15,2 % |
27,8 % |
|
6 |
12,8 % |
13,0 % |
24,1 % |
|
5 |
10,6 % |
10,9 % |
20,3 % |
|
4 |
8,5 % |
8,7 % |
16,5 % |
|
3 |
6,4 % |
6,5 % |
12,5 % |
|
2 |
4,3 % |
4,3 % |
8,4 % |
|
1 |
2,1 % |
2,2 % |
4,3 % |
📌 Bemærk: Der findes en meget nem metode til at beregne sandsynligheden for outs, så du kan gøre det direkte ved bordet. Det kaldes generelt "fire og to"-reglen. Efter floppet skal spilleren blot gange antallet af outs med 4 for at finde sandsynligheden for turn og river. Hvis han ikke får kortet på turn, skal han blot gange antallet af outs med to for at få den omtrentlige sandsynlighed for at få kortet på river.
Igen kan vi bruge eksemplet med 4 kort i samme farve efter floppet. Så dine outs er 9 kort, og sandsynligheden for en flush efter turn og river er 36 % (9x4). Lad os sige, at du ikke får et kort på turen. I så fald ganges outs med to og vi finder ud af, at vi har en 18 % (9x2) chance for at løbe tør for kort i den pågældende farve på river. Som du kan se ved at sammenligne tabellen, er denne metode virkelig enkel, men på den anden side upræcis, men den kan bruges.

 DK
DK  English
English  čeština
čeština  Polski
Polski  Slovenčina
Slovenčina  Русский
Русский  Deutsch
Deutsch  Slovenski
Slovenski  Dutch
Dutch  Svenska
Svenska  Português
Português  Italiano
Italiano  Español
Español  Français
Français  Suomalainen
Suomalainen  Български
Български  Românesc
Românesc  Magyar
Magyar  Eesti
Eesti  Ελληνική
Ελληνική  Latviešu
Latviešu  Lietuvių
Lietuvių  やまと
やまと  中国
中国  Türkçe
Türkçe  ID
ID  Українська
Українська  한국어
한국어  Norsk
Norsk 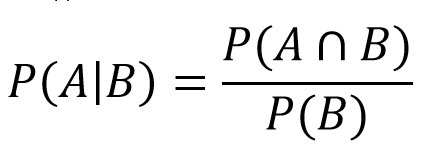


Du skal være logget ind for at tilføje en kommentar