Probabilidad y juegos de casino
 Peter Sommer
Peter Sommer
¿Entiendes tus posibilidades? Si vas a jugar en un casino, debes asegurarte de conocer tus posibilidades y entenderlas perfectamente. ¿Por qué? Porque la probabilidad es el motor que hace funcionar los casinos. Sin la probabilidad, la industria del juego no sería posible.
El azar es simplemente la probabilidad de que algo ocurra. La probabilidad forma parte de nuestra vida cotidiana. Cuando decidimos cruzar una calle muy transitada con el semáforo en rojo, existe la posibilidad de que nos atropelle un coche, pero a cambio tenemos la oportunidad de cruzar la calle más rápido y ganar algo de tiempo.
Cuando apostamos, calculamos la probabilidad de que se produzca un determinado acontecimiento para formular nuestra apuesta. Es en estos casos cuando calculamos la probabilidad.
💡 Ejemplo de probabilidad
Supongamos que tenemos una bolsa que contiene cuatro bolas de las cuales sólo una es roja y las otras tres son azules. La probabilidad de sacar sólo la bola roja sin mirar es de 1 entre 4.
Hay varias formas de expresar la probabilidad. También podemos decir que hay una probabilidad de 3 en 1 contra el rojo, porque en promedio sacamos tres bolas azules por cada bola roja extraída.
También podemos expresar nuestras posibilidades en forma de porcentaje, de modo que nuestra probabilidad de sacar una bola roja es del 25% si hay un 100% de posibilidades de sacar una bola. Así que 100 dividido entre cuatro nos da el 25%.
La probabilidad de sacar una bola azul es del 75% si hay tres bolas azules con un 25% de probabilidad de sacar.
Probabilidad de los juegos de casino
El casino opera bajo el principio de ofrecer probabilidades que no son tan buenas considerando nuestro resultado a largo plazo.
El ejemplo de una bolsa de globos es una forma sencilla de mostrar cómo funciona un casino. Digamos que un casino ofrece probabilidades de 3 para sacar una bola roja. Si usted apuesta 5 dólares, entonces en promedio, en cuatro intentos sacará su bola azul 3 veces y perderá 15 dólares, y en la cuarta vez sacará su bola roja y ganará 10 dólares, pero el casino seguirá estando en negro por 5 dólares.
Todos los juegos de azar se basan en la probabilidad. Cualquier jugador experimentado te lo dirá. Por lo tanto, es esencial estar familiarizado con estos números y saber cómo trabajar con ellos. Así que aquí le mostraremos cómo calcular la probabilidad en los juegos de azar. Si entiendes el principio correctamente, puedes utilizarlo para calcular la probabilidad de cualquier otra cosa.
Probabilidad en la ruleta
La ruleta es como la rueda de la fortuna. ¿Y sabes por qué? Sólo hacen falta tres palabras para explicarlo: la teoría de los grandes números. Toda persona que dirige un casino o produce juegos de casino en línea conoce muy bien esta teoría. Porque está directamente relacionado con sus ingresos. Y gracias a ello, el casino también gana siempre a los apostantes a largo plazo. Todo está relacionado con la probabilidad y la ventaja de la casa.
📌 Nota: Todos los números del artículo se refieren a la Ruleta Europea - por lo que contamos 37 números.
Cómo escribir la probabilidad
Hay varias formas de escribir la probabilidad. Probablemente el más conocido sea el de los porcentajes. Además, se utilizan expresiones que utilizan una fracción o un cociente.
- Expresado como un porcentaje (%) - no hay mucho que añadir aquí, pero sólo para completar, este es el porcentaje para el evento seleccionado. Se calcula como (Parte/Total)*100. Por ejemplo, la probabilidad de acertar el número seleccionado en una ruleta (Recta): 1/37*100=2,7%.
- Expresión mediante fracciones (1/x) - Al expresar la probabilidad mediante una fracción, decimos que el fenómeno se produce 1 vez de cada X ensayos. En la expresión numérica, nos basamos en el cálculo de porcentajes. Si consideramos el ejemplo de 1/37 anterior, esto significa que un número seleccionado estadísticamente en la ruleta caerá 1 vez en 37 giros.
- Expresión por ratio (x a 1) - Cada vez que ocurre X, el fenómeno seleccionado ocurre 1 veces. Aquí también nos quedamos con la probabilidad del número seleccionado en la ruleta. En este caso, la proporción se escribirá como 36 a 1. Esto significa que después de cada 36 giros en los que el número no caiga, habrá un caso en el que el número seleccionado caiga.
📌 Nota: Como dice la teoría de los grandes números, la probabilidad es esencialmente un límite matemático. Con más y más pruebas, te acercas cada vez más al resultado calculado.
Como puedes ver, las expresiones usando fracciones y usando cocientes son muy similares. La única diferencia es que una fracción cuenta todos los giros, mientras que un ratio divide el total de giros en dos categorías.
Tabla de probabilidades para las apuestas individuales en la ruleta
|
Apuesta |
Extraído de |
Ratio |
Porcentajes |
|
Una apuesta directa |
1/2,055 |
1,055 a 1 |
48,6 % |
|
Columna |
1/3,08 |
2,08 a 1 |
32,4 % |
|
La Docena |
1/3,08 |
2,08 a 1 |
32,4 % |
|
Línea Seis |
1/6,17 |
5,17 a 1 |
16,2 % |
|
Rincón |
1/9,25 |
8,25 a 1 |
10,8 % |
|
Calle |
1/12,33 |
11,33 a 1 |
8,1 % |
|
Dividir |
1/19,5 |
18,5 a 1 |
5,4 % |
|
Recto |
1/37 |
36 a 1 |
2,7 % |
Probabilidad de una apuesta directa
También podría ser interesante una comparación matemática para la repetición del fenómeno seleccionado. Para este caso hemos elegido una apuesta directa, concretamente por ejemplo una apuesta al rojo. Entonces, ¿cuál será la probabilidad cambiante del rojo 5 veces seguidas, por ejemplo?
|
Número de giros |
Ratio |
Porcentajes |
|
1 |
1,06 a 1 |
48,6 % |
|
2 |
3,23 a 1 |
23,7 % |
|
3 |
7,69 a 1 |
11,5 % |
|
4 |
16,9 a 1 |
5,6 % |
|
5 |
35,7 a 1 |
2,73 % |
|
6 |
74,4 a 1 |
1,33 % |
|
7 |
154 a 1 |
0,65 % |
|
8 |
318 a 1 |
0,31 % |
|
9 |
654 a 1 |
0,15 % |
|
10 |
1 346 a 1 |
0,074 % |
|
15 |
49 423 a 1 |
0,002 % |
|
20 |
1 813 778 a 1 |
0,000055 % |
Como se puede observar, a medida que aumenta el número de giros, la probabilidad de este fenómeno disminuye rápidamente. Sin embargo, hay que tener en cuenta que estas probabilidades describen el fenómeno en su conjunto. El generador de números aleatorios no tiene en cuenta los resultados anteriores, por lo que aunque una serie de juegos en la que el rojo acierte 20 veces seguidas ocurra una vez cada 1,813 millones de juegos, una ronda de 21 juegos tendrá la misma ventaja de la casa y la misma probabilidad (es decir, el 48,6%) que cualquier otra ronda de juegos.
A menudo, en este caso, se puede encontrar el término Falacia del Jugador, donde el apostador cree que si un color es golpeado varias veces en una fila, hay una mayor probabilidad de que el otro color sea golpeado en la siguiente tirada. En realidad, no es así. El caso más famoso de esta falacia se observó en 1913 en el Casino de Montecarlo, cuando el negro cayó 26 veces seguidas en la ruleta, y durante casi toda esta increíble racha, e incluso después de que terminara, la gente apostó frenéticamente al rojo. Fue entonces cuando el casino ganó mucho dinero.
📌 Nota: La probabilidad de que un color acierte 26 veces seguidas es del 0,000000730870% y ocurre una vez en 67 millones de partidas.
Cómo calcular la probabilidad de la ruleta
¿Desea conocer más probabilidades para las apuestas individuales? Intenta calcularlos tú mismo. Trabajar con porcentajes y probabilidades no es muy complicado. En general, lo más fácil es empezar con las fracciones y utilizarlas para calcular más porcentajes y ratios. Por ejemplo, si se quiere calcular la probabilidad en una fracción para una situación en la que el rojo es rojo, se hace lo siguiente:
Número total de rojos en el campo de juego/Número total de campos de juego = 18/37
Probabilidad de un giro
Una vez más, se aplica una regla sencilla. Simplemente calcule el número de campos que le darán una victoria y divídalo por el número total de campos.
Por ejemplo:
- Color - 18/37
- Sudá/Lichá - 18/37
- Docena - 12/37
- Número 0 - 1/37
- Negro y par - 9/37 (sólo hay 9 números en el campo de juego que son a la vez negros y pares)
- Docena y columna - 4/37 (sólo hay 4 números en una docena y en una columna)
Al igual que la probabilidad de ganar, se puede calcular la probabilidad de perder. Sólo hay que contar el número de campos no ganadores y dividirlo de nuevo entre el número total de campos. Por ejemplo, la probabilidad de perder si se apuesta al rojo es de 19/37 (18 campos negros + cero verde).
📌 Nota: Para reducir una fracción a 1/x, basta con dividir el numerador y el denominador entre el numerador. Por ejemplo, 18/37 (se dividen ambos números por 18) será 1/2,055 después del ajuste. Y esto significa que por cada 2,055 vueltas, una vuelta resultará en un rojo o un negro.
Probabilidad de giros múltiples
Una vez que haya dominado el cálculo de las tiradas simples, el cálculo de la probabilidad de las tiradas múltiples es muy sencillo. Sólo hay que multiplicar las fracciones individuales entre sí.
Ejemplos:
- giro - apuesta al rojo = 18/37
- giro - apuesta por docena = 12/37
Probabilidad de ganar ambas rondas = (18/37)*(12/37)=1/6,34 o 15,77% o 5,34 a 1
- giro - apuesta directa - 1/37
- giro - apuesta directa - 1/37
Probabilidad de ganar ambas rondas = (1/37)*(1*37)=1/1369 o 0,073% o 1368 a 1
- giro - apuesta a negro e impar 9/37
- giro - apuesta por el par 18/37
- giro - apuesta de columna 12/37
Probabilidad de ganar las 3 rondas = (9/37)*(18/37)*(12/37)=1/26,06 o 3,84% o 25,06 a 1 La conversión real entre las entradas es, de nuevo, muy fácil. Los porcentajes se obtienen dividiendo la fracción en la forma 1/x y multiplicando por 100. Se obtiene la notación proporcional en la forma de X a 1 restando 1 del denominador, que es la ronda ganadora del total. Véanse los ejemplos que aparecen en la parte superior del párrafo.
Probabilidad de los dados
Los dados son otro juego de azar en el que es relativamente fácil calcular las probabilidades. Antes de entrar en el cálculo de las probabilidades de ganar en los dados, echemos un vistazo a la probabilidad de las propias tiradas de dados.
Los dados tienen 6 caras. Por lo tanto, la probabilidad de que cualquier número caiga es de 1/6. Los dados se juegan tradicionalmente con dos dados. La probabilidad de que dos números cualesquiera se combinen es, por tanto, de 2/36. Sin embargo, no nos interesan tanto los números concretos como la suma de esos números, que es mucho más importante en los dados. De nuevo, utilizaremos la fórmula: número de combinaciones ganadoras/número de todas las combinaciones.
Digamos que queremos saber la probabilidad de la suma de 7. Combinaciones ganadoras: (1-6), (2-4), (3-3), (4-2), (6-1). Como puede ver, hay un total de 6 combinaciones diferentes en las que puede salir la suma de 7 en dos dados. Y como el número de todas las combinaciones es 36, la probabilidad de 7 es 6/36=0,1666
De este modo, se pueden calcular fácilmente todos los demás resultados posibles.
|
Total |
Probabilidad |
|
2 |
1/36 |
|
3 |
2/36 |
|
4 |
3/36 |
|
5 |
4/36 |
|
6 |
5/36 |
|
7 |
6/36 |
|
8 |
5/36 |
|
9 |
4/36 |
|
10 |
3/36 |
|
11 |
2/36 |
|
12 |
1/36 |
Probabilidades de ganar en los dados
Brevemente, echemos un vistazo a las reglas de los dados. La apuesta más común es la línea de pase.
- Si sacas un 7 u 11, ganas
- Si sacas un 2, 3 o 12, pierdes
- En otros casos (4, 5, 6, 8, 9 o 10) se determina un punto y se tira hasta que se vuelva a sacar ese punto (ganar) o se saque un 7 (perder)
Primero calculamos la probabilidad de ganar antes de determinar el punto. La probabilidad de acertar 7 es de 6/36 y la de acertar 11 es de 2/36. Estas dos fracciones deben sumarse para obtener 3/36+2/36 = 2/9 = 0,2222.
Pasamos ahora a la situación en la que se determina un punto. Es decir, cuando el punto es 4, 5, 6, 8, 9 o 10. Empecemos con un total de 4.
Si sale un 4, se determina un punto y el jugador tira hasta que salga un 4 o un 7. Aquí es donde entramos en el terreno de la probabilidad condicional. Esto nos dice cuál es la probabilidad del suceso A si el suceso B ocurre al mismo tiempo. En nuestro caso, será cuál es la probabilidad de que ganemos (saca un 4) si la ronda termina (saca un 4 o un 7). A continuación, introducimos estos valores en la fórmula:
- P(A) = suma de caídas de 4: 3/36
- P(A∩B) = después de los ajustes encontramos que es igual a A
- P(B) = Caídas 4 o 7: 3/36 + 6/36 = 9/36
De ello se desprende que:
- P(4|4 o 7) = (3/36)/(9/36) = 1/3
De forma similar podemos calcular las sumas de 5, 6, 8, 9 y 10
- P(5|5 o 7) = (4/36)/(10/36) = 2/5
- P(6|6 ó 7) = (5/36)/(11/36) = 5/11
- P(8|8 o 7) = (5/36)/(11/36) = 5/11
- P(9|9 o 7) = (4/36)/(10/36) = 2/5
- P(10|10 o 7) = (3/36)/(9/36) = 1/3
Ahora podemos calcular la probabilidad de ganar como la probabilidad de la tirada original cuando se determinó el punto y la siguiente tirada cuando el jugador ganó.
- Tirada original 4 x P(4|4 o 7) = 3/36 x 1/3 = 1/36
- Tirada original 5 x P(5|5 o 7) = 4/36 x 2/5 = 2/45
- Tirada original 6 x P(6|6 o 7) = 5/36 x 5/11 = 25/396
- Tirada original 8 x P(8|8 o 7) = 5/36 x 5/11 = 25/396
- Tirada original 9 x P(9|9 o 7) = 4/36 x 2/5 = 2/45
- Tirada original 10 x P(10|10 o 7) = 3/36 x 1/3 = 1/36
Todas estas fracciones nos dan la probabilidad de ganar si la primera tirada es 4, 5, 6, 8, 9 o 10. Si quiere saber la probabilidad total de ganar en una apuesta de línea de pase, tiene que sumarlas todas y añadir la probabilidad de ganar antes del punto (saca un 7 o un 11 - 2/9).
2/9 + 1/36 + 2/45 + 25/396 + 25/396 + 2/45 + 1/36 = 244/495
Porque 244/495 es exactamente el 49,3%. Eso es algo menos del 50%. De hecho, probablemente no encontrará una mejor oportunidad de ganar con un pago de 1 en 1. Excepto quizás el blackjack, si sabes contar cartas.
Probabilidad de Blackjack
El blackjack es el juego de azar en el que más importan las probabilidades. En el blackjack, puedes influir en la ventaja de la casa con tu habilidad y conocimientos. Sólo hay que conocer la estrategia óptima para ello, y si sabes contar las cartas, incluso jugarás con ventaja. En realidad, no necesitas conocer todas las probabilidades específicas, porque todos estos cálculos ya han sido realizados por matemáticos antes que tú, que idearon todas las tácticas y estrategias para el blackjack.
Sin embargo, por interés, mostraremos cómo calcular la probabilidad de algunos fenómenos importantes en el blackjack.
Si consideramos el problema de la probabilidad desde la perspectiva de una baraja de cartas, está claro que el número de resultados posibles aumenta rápidamente. El blackjack se juega con una baraja de 52 cartas, 4 palos y 13 valores. Esto da las siguientes probabilidades:
- Saco un as de la baraja (o cualquier carta individual): 4/52=0,0769 (7,69%)
- Saco una pica de la baraja: 13/52=0,25 (25%)
Sin embargo, a diferencia del lanzamiento de una moneda, la ruleta o las máquinas tragaperras, por ejemplo, una baraja de cartas tiene algo de "memoria". O mejor dicho, significa que los resultados anteriores tienen un efecto en los movimientos actuales y futuros. Esto se debe al hecho de que se ha eliminado una carta del mazo y esto cambia la situación inicial. Veamos un ejemplo en el que la primera carta extraída de una baraja de 52 cartas fue un as (7,69% de posibilidades). La probabilidad de que se vuelva a sacar un As como segunda carta de la baraja será ahora diferente. Tras la primera extracción, el número de ases ha bajado a 3 y el número de cartas a 51.
Probabilidad para el blackjack natural
Lo que a todo jugador le interesa en primer lugar es la probabilidad del blackjack. Es decir, cuáles son las posibilidades de que un jugador obtenga un as y una carta de diez justo al comienzo de la ronda, es decir, un natural.
Esta situación puede darse de dos maneras, y si sumamos las dos formas, obtenemos nuestras probabilidades en el blackjack:
📌 Nota: Estamos contando para el blackjack de una sola baraja. Así que 52 cartas, 4 ases y 16 dieces. La carta del repartidor no es visible, por lo que no afectará a la probabilidad.
- El jugador recibe el primer as y una carta de diez
El jugador recibe la primera carta de As con una probabilidad de 4/52. Así que el jugador debe conseguir la segunda carta con un diez, y para ello las probabilidades son de 16/51. Estas dos probabilidades deben multiplicarse para obtener 16/663.
- El jugador recibe la primera carta de diez y un as
La probabilidad de que un jugador reciba la primera carta con un valor de 10 es de 16/52. Las probabilidades de que un jugador obtenga un As después de eso son de 4/51. Después de multiplicar, obtenemos 16/663.
Si queremos saber la probabilidad de obtener un blackjack sólo tenemos que sumar estos dos fenómenos. Así que 16/663 + 16/663 = 32/663 = 4,827%. En otras palabras, un jugador obtiene un blackjack aproximadamente una vez cada 20 manos. Puede calcular la probabilidad para las mesas con varios mazos de forma similar, lo que ya hemos hecho por usted.
|
Número de paquetes |
Probabilidad |
|
1 |
4,827 % |
|
2 |
4,780 % |
|
3 |
4,764 % |
|
4 |
4,757 % |
|
5 |
4,752 % |
|
6 |
4,749 % |
Probabilidad de quiebra
También puede ser interesante saber cuáles son las probabilidades de que se produzca un fracaso. Una vez más, nos centraremos en una situación de ejemplo en la que se juega sólo con el crupier en una mesa de una sola baraja. Veamos una situación muy simple en la que un jugador tiene 2 cartas con un valor de 10 en total por lo que tiene 20 puntos. En una situación en la que el jugador obtiene una tercera carta, ya se han jugado 3 cartas del mazo. Esto deja 49 cartas en la baraja. De estas 49 cartas, sólo 4 ases te ayudarán. De estas 49, 45 tarjetas no son deseadas. Por lo tanto, las probabilidades de que se produzca un fracaso son 45/49=0,9183673.
Se pueden calcular otras probabilidades de forma similar. Siempre hay que ser capaz de imaginar la situación correctamente. Eso es todo.
|
Valor de la mano |
Probabilidad de bustos |
|
21 |
100 % |
|
20 |
92 % |
|
19 |
85 % |
|
18 |
77 % |
|
17 |
69 % |
|
16 |
62 % |
|
15 |
58 % |
|
14 |
56 % |
|
13 |
39 % |
|
12 |
31 % |
|
11 menos |
0 % |
Veamos a continuación la probabilidad de que la banca se pase con cada carta.
|
Valor de la mano |
Probabilidad de bustos |
|
2 |
35,30 % |
|
3 |
37,56 % |
|
4 |
40,28 % |
|
5 |
42,89 % |
|
6 |
42,08 % |
|
7 |
25,99 % |
|
8 |
23,86 % |
|
9 |
23,34 % |
|
10, J, Q, K |
21,43 % |
|
As |
11,65 % |
Probabilidad de póquer
El póker es otro juego de cartas en el que la probabilidad es extremadamente importante. Entre otras cosas. Así que echemos un vistazo a las posibilidades que tienes en el póker.
Probabilidad pre-flop
Ahora que hemos esbozado cómo funciona la probabilidad en una baraja, pasemos a las aplicaciones prácticas. En primer lugar, mostraremos cómo calcular la probabilidad de quedarse sin parejas en una mano. (por ejemplo, los tan mentados Ases). En este caso, tenemos que multiplicar las probabilidades entre sí.
(4/52) x (3/51) = (12/2652) = (1/221) = 0,004524 (0,45 %)
📌 Nota: Si juegas al póker en un casino que reparte unas 30 manos por hora, obtendrás una pareja de ases aproximadamente una vez cada 7 horas y media de juego.
Entonces, ¿cuáles son las posibilidades de obtener alguna de las 13 parejas posibles al repartir? Podemos suponer que las probabilidades son de 1/221 por pareja individual (véase la fórmula anterior). Puede haber 13 de estos pares en total, por lo que la fórmula de cálculo será 13/221=0,0588. Así que puedes esperar un par más o menos cada 35 partidos.
Probabilidad en el póker jugador contra jugador
Sin embargo, el póquer es un juego multijugador, que se suele jugar contra los demás. Así que aquí hay una selección de las situaciones pre-flop más comunes.
|
Tu mano |
Mano de su oponente |
Probabilidad de ganar |
|
Par alto |
Dos cartas bajas |
83 % |
|
Par alto |
Par bajo |
82 % |
|
Pares del medio |
Carta alta, carta baja |
71 % |
|
Dos cartas altas |
Dos cartas bajas |
63 % |
|
Dos cartas altas |
Par bajo |
55 % |
Cálculo de la probabilidad por "outs"
Si consigues ver las cartas del flop, seguro que te interesa más saber qué posibilidades tienes de mejorar tu mano. En este caso, hablaremos de los llamados "outs". En el póker, este término se refiere a cualquier carta que pueda ayudarte. Un caso tan común puede ser cuando un jugador tiene dos cartas de un palo y aparecen dos cartas más del mismo palo en el flop. El jugador tiene entonces 4 cartas para el flush y por lo tanto tiene 9 outs, dejando 9 cartas con las que formar un flush.
|
Número de salidas |
Flop - Turn |
Vuelta - Río |
Gira un río |
|
20 |
42,6 % |
43,5 % |
67,5 % |
|
19 |
40,4 % |
41,3 % |
65,0 % |
|
18 |
38,3 % |
39,1 % |
62,4 % |
|
17 |
36,2 % |
37,0 % |
59,8 % |
|
16 |
34,0 % |
34,8 % |
57,0 % |
|
15 |
31,9 % |
32,6 % |
54,1 % |
|
14 |
29,8 % |
30,4 % |
51,2 % |
|
13 |
27,7 % |
28,3 % |
48,1 % |
|
12 |
25,5 % |
26,1 % |
45,0 % |
|
11 |
23,4 % |
23,9 % |
41,7 % |
|
10 |
21,3 % |
21,7 % |
38,4 % |
|
9 |
19,1 % |
19,6 % |
35,0 % |
|
8 |
17,0 % |
17,4 % |
31,5 % |
|
7 |
14,9 % |
15,2 % |
27,8 % |
|
6 |
12,8 % |
13,0 % |
24,1 % |
|
5 |
10,6 % |
10,9 % |
20,3 % |
|
4 |
8,5 % |
8,7 % |
16,5 % |
|
3 |
6,4 % |
6,5 % |
12,5 % |
|
2 |
4,3 % |
4,3 % |
8,4 % |
|
1 |
2,1 % |
2,2 % |
4,3 % |
📌 Nota: Existe un método muy sencillo para calcular la probabilidad de outs, por lo que puedes hacerlo directamente en la mesa. Generalmente se denomina la regla del "cuatro y dos". Después del flop, el jugador simplemente multiplica el número de salidas por 4 para encontrar la probabilidad para el turn y el river. Si no consigue la carta en el turn, simplemente multiplica el número de outs por dos para obtener la probabilidad aproximada de conseguir la carta en el river.
De nuevo, podemos utilizar el ejemplo de tener 4 cartas del mismo palo después del flop. Así que tus outs son 9 cartas y la probabilidad de un flush tras el turn y el river es del 36% (9x4). Digamos que no consigues una carta en el turno. En este caso, multiplicamos los outs por dos y encontramos que tenemos un 18% (9x2) de posibilidades de quedarnos sin cartas del palo en el river. Como se puede ver comparando la tabla, este método es realmente sencillo, pero por otro lado inexacto, sin embargo se puede utilizar.

 ES
ES  English
English  čeština
čeština  Polski
Polski  Slovenčina
Slovenčina  Русский
Русский  Deutsch
Deutsch  Slovenski
Slovenski  Dutch
Dutch  Svenska
Svenska  Português
Português  Italiano
Italiano  Français
Français  Suomalainen
Suomalainen  Български
Български  Românesc
Românesc  Magyar
Magyar  Eesti
Eesti  Ελληνική
Ελληνική  Latviešu
Latviešu  Lietuvių
Lietuvių  やまと
やまと  中国
中国  Dansk
Dansk  Türkçe
Türkçe  ID
ID  Українська
Українська  한국어
한국어  Norsk
Norsk 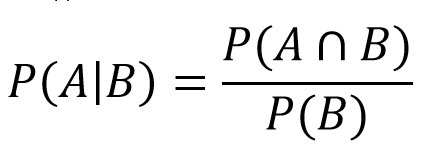


Tienes que estar conectado para añadir un comentario