Permainan probabilitas dan kasino
 Peter Sommer
Peter Sommer
Apakah Anda memahami peluang Anda? Jika Anda akan bermain di kasino, Anda harus memastikan bahwa Anda mengetahui peluang Anda dan memahaminya dengan baik. Kenapa? Karena probabilitas adalah mesin yang membuat kasino bekerja. Tanpa probabilitas, industri perjudian tidak akan mungkin ada.
Peluang adalah probabilitas bahwa sesuatu akan terjadi. Probabilitas adalah bagian dari kehidupan kita sehari-hari. Ketika kita memutuskan untuk menyeberang jalan yang sibuk di lampu merah, ada kemungkinan kita akan tertabrak mobil, tetapi sebagai gantinya, kita memiliki kesempatan untuk menyeberang jalan lebih cepat dan mendapatkan waktu luang.
Ketika kita bertaruh, kita memperkirakan probabilitas terjadinya suatu peristiwa tertentu untuk merumuskan taruhan kita. Dalam kasus-kasus inilah kami menghitung probabilitas.
💡 Contoh probabilitas
Katakanlah kita memiliki sebuah tas yang berisi empat bola yang hanya satu berwarna merah dan tiga lainnya berwarna biru. Kemungkinan menarik bola merah saja tanpa melihat adalah 1 banding 4.
Ada beberapa cara untuk menyatakan probabilitas. Kita juga dapat mengatakan bahwa ada peluang 3 banding 1 melawan warna merah, karena rata-rata kita menarik tiga bola biru untuk setiap bola merah yang ditarik.
Kita juga dapat menyatakan peluang kita sebagai persentase, jadi peluang kita untuk menggambar bola merah adalah 25% jika ada 100% peluang untuk menggambar bola. Jadi, 100 dibagi empat menghasilkan 25%.
Peluang untuk menarik bola biru adalah 75% jika ada tiga bola biru dengan peluang 25% untuk keluar.
Probabilitas permainan kasino
Kasino beroperasi dengan prinsip menawarkan peluang yang tidak terlalu bagus mengingat hasil jangka panjang kami.
Contoh sekantong balon adalah cara sederhana untuk menunjukkan cara kerja kasino. Katakanlah sebuah kasino menawarkan peluang 3 untuk menarik bola merah. Jika Anda bertaruh $ 5, maka rata-rata, dalam empat kali percobaan Anda akan menarik bola biru Anda 3 kali dan kalah $ 15, dan pada kali keempat Anda menarik bola merah Anda dan menang $ 10, tetapi kasino masih akan berada dalam posisi kalah $ 5.
Semua perjudian hanyalah tentang probabilitas. Setiap penjudi berpengalaman akan memberi tahu Anda hal itu. Oleh karena itu, sangat penting untuk mengenal angka-angka ini dan mengetahui cara menggunakannya. Jadi di sini kami akan menunjukkan kepada Anda cara menghitung probabilitas dalam perjudian. Jika Anda memahami prinsip ini dengan benar, Anda dapat menggunakannya untuk menghitung probabilitas apa pun.
Probabilitas di roulette
Roulette seperti Roda Keberuntungan. Dan kau tahu kenapa? Hanya perlu 3 kata untuk menjelaskannya - Teori Angka Besar. Setiap orang yang menjalankan kasino atau membuat permainan kasino online mengetahui teori ini dengan sangat baik. Karena hal ini terkait langsung dengan penghasilannya. Dan berkat itu, kasino selalu menang atas para petaruh dalam jangka panjang. Semuanya terkait dengan probabilitas dan tepi rumah.
📌 Catatan: Semua angka dalam artikel ini mengacu pada Roulette Eropa - jadi kami menghitung 37 angka.
Bagaimana cara menulis probabilitas
Ada beberapa cara untuk menulis probabilitas. Mungkin yang paling terkenal adalah persentase. Selain itu, ekspresi yang menggunakan pecahan atau rasio juga digunakan.
- Dinyatakan sebagai persentase (%) - tidak banyak yang bisa ditambahkan di sini, tetapi hanya untuk kelengkapan, ini adalah persentase untuk acara yang dipilih. Ini dihitung sebagai (Bagian/Total)*100. Misalnya, probabilitas untuk mendapatkan nomor yang dipilih pada roda roulette (Lurus): 1/37 * 100 = 2,7%
- Ekspresi menggunakan pecahan (1/x) - Ketika mengekspresikan probabilitas menggunakan pecahan, kita mengatakan bahwa fenomena tersebut terjadi 1 kali dari X percobaan. Dalam ekspresi numerik, kami mengandalkan penghitungan persentase. Jika kita mempertimbangkan contoh 1/37 di atas, ini berarti bahwa angka yang dipilih secara statistik pada roda roulette akan jatuh 1 kali dalam 37 putaran.
- Ekspresi dengan rasio (x banding 1) - Setiap kali X terjadi, fenomena yang dipilih terjadi 1 kali. Di sini sekali lagi kita tetap menggunakan probabilitas untuk nomor yang dipilih di roulette. Dalam hal ini, rasio akan dituliskan sebagai 36 banding 1. Ini berarti bahwa setelah setiap 36 putaran di mana angka tidak jatuh, akan ada satu contoh di mana angka yang dipilih jatuh.
📌 Catatan: Seperti yang dikatakan oleh teori bilangan besar, probabilitas pada dasarnya adalah batas matematis. Dengan semakin banyak uji coba, Anda secara realistis semakin mendekati hasil yang dihitung.
Seperti yang Anda lihat, ekspresi menggunakan pecahan dan menggunakan rasio sangat mirip. Satu-satunya perbedaan adalah bahwa pecahan menghitung semua putaran, sedangkan rasio membagi total putaran menjadi dua kategori.
Tabel probabilitas untuk taruhan individu dalam roulette
|
Taruhan |
Dikutip dari |
Rasio |
Persentase |
|
Taruhan lurus |
1/2,055 |
1,055 banding 1 |
48,6 % |
|
Kolom |
1/3,08 |
2.08 banding 1 |
32,4 % |
|
Selusin |
1/3,08 |
2.08 banding 1 |
32,4 % |
|
Enam baris |
1/6,17 |
5,17 banding 1 |
16,2 % |
|
Sudut |
1/9,25 |
8,25 banding 1 |
10,8 % |
|
Jalan |
1/12,33 |
11,33 banding 1 |
8,1 % |
|
Membagi |
1/19,5 |
18,5 banding 1 |
5,4 % |
|
Lurus |
1/37 |
36 banding 1 |
2,7 % |
Probabilitas untuk taruhan lurus
Perbandingan matematis untuk pengulangan fenomena yang dipilih juga bisa menarik. Untuk kasus ini kami telah memilih taruhan lurus, khususnya taruhan pada warna merah. Jadi, berapa probabilitas perubahan warna merah 5 kali berturut-turut, misalnya?
|
Jumlah putaran |
Rasio |
Persentase |
|
1 |
1,06 banding 1 |
48,6 % |
|
2 |
3.23 banding 1 |
23,7 % |
|
3 |
7,69 banding 1 |
11,5 % |
|
4 |
16,9 banding 1 |
5,6 % |
|
5 |
35,7 banding 1 |
2,73 % |
|
6 |
74,4 banding 1 |
1,33 % |
|
7 |
154 banding 1 |
0,65 % |
|
8 |
318 banding 1 |
0,31 % |
|
9 |
654 banding 1 |
0,15 % |
|
10 |
1 346 banding 1 |
0,074 % |
|
15 |
49 423 banding 1 |
0,002 % |
|
20 |
1.813.778 hingga 1 |
0,000055 % |
Seperti yang dapat dilihat, ketika jumlah putaran meningkat, probabilitas fenomena ini menurun dengan cepat. Namun, perlu diingat bahwa probabilitas ini menggambarkan fenomena secara keseluruhan. Generator angka acak tidak memperhitungkan hasil sebelumnya, jadi meskipun seri permainan di mana angka merah muncul 20 kali berturut-turut terjadi sekali dalam 1,813 juta permainan, putaran permainan ke-21 akan memiliki keunggulan dan probabilitas yang sama (yaitu 48,6%) seperti setiap putaran permainan lainnya.
Seringkali dalam kasus ini, seseorang dapat menemukan istilah Kekeliruan Pemain, di mana petaruh percaya bahwa jika satu warna dipukul beberapa kali berturut-turut, ada kemungkinan lebih tinggi bahwa warna lain akan dipukul di putaran berikutnya. Kenyataannya, tidak demikian. Kasus yang paling terkenal dari kekeliruan ini terjadi pada tahun 1913 di Kasino Monte Carlo, ketika warna hitam jatuh 26 kali berturut-turut di roda roulette, dan hampir selama keseluruhan rentetan yang luar biasa ini, dan bahkan setelah berakhir, orang-orang bertaruh dengan panik pada warna merah. Saat itulah kasino menghasilkan banyak uang.
📌 Catatan: Probabilitas suatu warna terkena 26 kali berturut-turut adalah 0,000000730870% dan terjadi satu kali dalam 67 juta permainan.
Bagaimana cara menghitung probabilitas roulette
Ingin tahu lebih banyak peluang untuk taruhan individu? Cobalah menghitungnya sendiri. Bekerja dengan persentase dan probabilitas tidaklah terlalu rumit. Umumnya, cara termudah adalah memulai dengan pecahan dan menggunakannya untuk menghitung persentase dan rasio lebih lanjut. Misalnya, jika Anda ingin menghitung probabilitas dalam pecahan untuk situasi di mana warna merah adalah merah, lakukan hal berikut:
Jumlah total kartu merah di lapangan permainan/Jumlah total lapangan permainan = 18/37
Probabilitas untuk satu putaran
Sekali lagi, aturan sederhana berlaku di sini. Cukup hitung jumlah bidang yang akan memberi Anda kemenangan dan membaginya dengan jumlah total bidang.
Sebagai contoh:
- Warna - 18/37
- Sudá/Lichá - 18/37
- Selusin - 12/37
- Angka 0 - 1/37
- Hitam dan genap - 9/37 (hanya ada 9 angka di lapangan yang berwarna hitam dan genap)
- Selusin dan kolom - 4/37 (hanya ada 4 angka dalam selusin dan kolom)
Sama seperti probabilitas menang, Anda dapat menghitung probabilitas kalah. Hitung saja jumlah bidang yang tidak menang dan bagi lagi dengan jumlah total bidang. Misalnya, kemungkinan kalah jika Anda bertaruh pada warna merah adalah 19/37 (18 bidang hitam + nol hijau).
📌 Catatan: Untuk mengurangi pecahan menjadi 1/x, cukup bagi pembilang dan penyebut dengan pembilang. Sebagai contoh, 18/37 (Anda membagi kedua angka dengan 18) akan menjadi 1/2,055 setelah penyesuaian. Jadi, ini berarti bahwa untuk setiap 2,055 putaran, satu putaran akan menghasilkan warna merah atau hitam.
Probabilitas untuk beberapa putaran
Setelah Anda menguasai perhitungan untuk putaran tunggal, menghitung probabilitas untuk beberapa putaran sangatlah sederhana. Kalikan saja pecahan-pecahan tersebut satu sama lain.
Contoh:
- putaran - bertaruh pada warna merah = 18/37
- putaran - taruhan per lusin = 12/37
Peluang untuk memenangkan kedua ronde = (18/37)*(12/37)=1/6.34 atau 15.77% atau 5.34 banding 1
- putaran - taruhan lurus - 1/37
- putaran - taruhan lurus - 1/37
Kemungkinan memenangkan kedua ronde = (1/37)*(1*37)=1/1369 atau 0.073% atau 1368 banding 1
- putaran - bertaruh pada hitam dan ganjil 9/37
- putaran - bertaruh pada genap 18/37
- putaran - taruhan per kolom 12/37
Kemungkinan memenangkan ketiga ronde = (9/37) * (18/37) * (12/37) = 1/26.06 atau 3.84% atau 25.06 banding 1
Konversi antar entri yang sebenarnya sangat mudah. Anda mendapatkan persentase dengan membagi pecahan dalam bentuk 1/x lalu mengalikannya dengan 100. Anda mendapatkan notasi proporsional dalam bentuk X ke 1 dengan mengurangi 1 dari penyebut, yang merupakan putaran kemenangan dari total. Lihat contoh di atas paragraf.
Probabilitas dadu
Craps adalah permainan peluang lain yang relatif mudah untuk menghitung peluangnya. Sebelum kita menghitung peluang menang di dadu, mari kita lihat probabilitas lemparan dadu itu sendiri.
Dadu memiliki 6 sisi. Oleh karena itu, peluang nomor apa pun akan jatuh adalah 1/6. Dadu secara tradisional dimainkan dengan dua dadu. Oleh karena itu, peluang kombinasi dua angka adalah 2/36. Namun, kami tidak begitu tertarik pada angka-angka tertentu melainkan jumlah dari angka-angka tersebut, yang jauh lebih penting dalam dadu. Sekali lagi, kita akan menggunakan rumus: jumlah kombinasi yang menang/jumlah semua kombinasi.
Katakanlah kita ingin mengetahui probabilitas untuk jumlah 7. Kombinasi yang menang: (1-6), (2-4), (3-3), (4-2), (6-1). Seperti yang Anda lihat, ada total 6 kombinasi berbeda di mana jumlah 7 dapat dilempar pada dua dadu. Dan karena jumlah semua kombinasi adalah 36, probabilitas 7 adalah 6/36 = 0,1666
Dengan cara ini, semua hasil yang mungkin terjadi dapat dengan mudah dihitung.
|
Total |
Probabilitas |
|
2 |
1/36 |
|
3 |
2/36 |
|
4 |
3/36 |
|
5 |
4/36 |
|
6 |
5/36 |
|
7 |
6/36 |
|
8 |
5/36 |
|
9 |
4/36 |
|
10 |
3/36 |
|
11 |
2/36 |
|
12 |
1/36 |
Peluang menang di dadu
Secara singkat, mari kita lihat aturan dadu. Taruhan yang paling umum adalah Pass Line.
- Jika Anda melempar 7 atau 11, Anda menang
- Jika Anda melempar angka 2, 3 atau 12, Anda kalah
- Dalam kasus lain (4, 5, 6, 8, 9 atau 10), sebuah poin ditentukan dan digulirkan sampai poin tersebut digulirkan lagi (menang) atau 7 digulirkan (kalah)
Pertama-tama kami menghitung probabilitas kemenangan sebelum menentukan poin. Peluang untuk mendapatkan angka 7 adalah 6/36 dan peluang untuk mendapatkan angka 11 adalah 2/36. Kedua pecahan ini kemudian harus ditambahkan bersama untuk menghasilkan 3/36 + 2/36 = 2/9 = 0,2222.
Sekarang kita mengalihkan perhatian kita ke situasi di mana suatu titik ditentukan. Yaitu, apabila titiknya adalah 4, 5, 6, 8, 9 atau 10. Mari kita mulai dengan total 4.
Jika angka 4 keluar, satu poin ditentukan dan pemain berguling sampai angka 4 atau 7 keluar. Di sinilah kita memasuki ranah probabilitas bersyarat. Ini memberi tahu kita berapa probabilitas kejadian A jika kejadian B terjadi pada waktu yang sama. Dalam kasus kita, ini akan menjadi probabilitas bahwa kita menang (menggulirkan 4) jika ronde berakhir (menggulirkan 4 atau 7). Kami kemudian memasukkan nilai-nilai ini ke dalam rumus:
- P(A) = Jumlah jatuh dari 4: 3/36
- P(A∩B) = setelah penyesuaian, kita menemukan bahwa itu sama dengan A
- P(B) = Jatuh 4 atau 7: 3/36 + 6/36 = 9/36
Oleh karena itu:
- P(4|4 atau 7) = (3/36) / (9/36) = 1/3
Dengan cara yang sama kita dapat menghitung jumlah 5, 6, 8, 9 dan 10
- P(5|5 atau 7) = (4/36) / (10/36) = 2/5
- P(6|6 atau 7) = (5/36) / (11/36) = 5/11
- P(8|8 atau 7) = (5/36) / (11/36) = 5/11
- P(9|9 atau 7) = (4/36) / (10/36) = 2/5
- P(10|10 atau 7) = (3/36) / (9/36) = 1/3
Sekarang kita dapat menghitung peluang menang sebagai probabilitas dari lemparan awal ketika poin ditentukan dan lemparan berikutnya ketika pemain menang.
- Gulungan asli 4 x P(4|4 atau 7) = 3/36 x 1/3 = 1/36
- Gulungan asli 5 x P(5|5 atau 7) = 4/36 x 2/5 = 2/45
- Gulungan asli 6 x P(6|6 atau 7) = 5/36 x 5/11 = 25/396
- Gulungan asli 8 x P(8|8 atau 7) = 5/36 x 5/11 = 25/396
- Gulungan asli 9 x P(9|9 atau 7) = 4/36 x 2/5 = 2/45
- Gulungan asli 10 x P(10|10 atau 7) = 3/36 x 1/3 = 1/36
Semua pecahan ini memberi kita probabilitas menang jika lemparan pertama adalah 4, 5, 6, 8, 9 atau 10. Jika Anda ingin mengetahui total peluang menang pada taruhan garis Pass, Anda harus menjumlahkan semuanya dan menambahkan peluang menang sebelum titik (menggulung 7 atau 11 - 2/9).
2/9 + 1/36 + 2/45 + 25/396 + 25/396 + 2/45 + 1/36 = 244/495
Karena 244/495 adalah tepat 49,3%. Itu hanya di bawah 50%. Faktanya, Anda mungkin tidak akan menemukan peluang yang lebih baik untuk menang dengan pembayaran 1 banding 1. Kecuali mungkin blackjack, jika Anda bisa menghitung kartu.
Probabilitas Blackjack
Blackjack adalah permainan peluang di mana peluang paling penting. Dalam blackjack, Anda dapat mempengaruhi tepi rumah dengan keterampilan dan pengetahuan Anda. Anda hanya perlu mengetahui strategi optimal untuk ini, dan jika Anda tahu cara menghitung kartu, Anda bahkan akan bermain dengan keuntungan pemain. Anda sebenarnya tidak perlu mengetahui semua probabilitas spesifik, karena semua perhitungan ini telah dilakukan oleh ahli matematika sebelum Anda yang menemukan semua taktik dan strategi untuk blackjack.
Namun, demi kepentingan Anda, kami akan menunjukkan cara menghitung probabilitas untuk beberapa fenomena penting dalam blackjack.
Jika kita melihat masalah probabilitas dari sudut pandang setumpuk kartu, jelas bahwa jumlah hasil yang mungkin terjadi meningkat dengan cepat. Blackjack dimainkan dengan setumpuk 52 kartu, 4 setelan dan 13 nilai. Ini memberikan peluang sebagai berikut:
- Saya menarik kartu As dari dek (atau kartu apa pun): 4/52=0,0769 (7,69%)
- Saya menarik sekop dari geladak: 13/52 = 0,25 (25%)
Namun, tidak seperti lemparan koin, roulette atau mesin slot misalnya, setumpuk kartu memiliki semacam "memori". Atau lebih tepatnya, ini berarti bahwa hasil sebelumnya berpengaruh pada pergerakan saat ini dan di masa depan. Hal ini disebabkan oleh fakta bahwa sebuah kartu telah dijatuhkan dari dek dan ini mengubah situasi awal. Mari kita lihat contoh di mana kartu As ditarik sebagai kartu pertama dari tumpukan kartu 52 kartu (peluang 7,69%). Probabilitas kartu As ditarik lagi sebagai kartu kedua dari tumpukan kartu sekarang akan berbeda. Setelah pengundian pertama, jumlah kartu As turun menjadi 3 dan jumlah kartu menjadi 51.
Probabilitas untuk blackjack alami
Apa yang pertama kali menarik bagi setiap pemain adalah probabilitas blackjack. Artinya, berapa peluang seorang pemain akan mendapatkan kartu As dan kartu sepuluh tepat di awal ronde - dengan kata lain, wajar.
Situasi ini dapat terjadi dalam dua cara, dan jika kita menjumlahkan kedua cara tersebut, kita akan mendapatkan peluang kita pada blackjack:
📌 Catatan: Kami menghitung untuk blackjack dek tunggal. Jadi 52 kartu, 4 kartu As dan 16 kartu puluhan. Kartu dealer tidak terlihat, sehingga tidak akan mempengaruhi probabilitas.
- Pemain menerima kartu As pertama dan kartu sepuluh
Pemain dibagikan kartu As pertama dengan probabilitas 4/52. Jadi pemain harus mendapatkan kartu kedua dengan nilai sepuluh, dan untuk itu peluangnya adalah 16/51. Kedua probabilitas ini harus dikalikan satu sama lain untuk mendapatkan 16/663.
- Pemain menerima sepuluh kartu pertama dan kartu As
Kemungkinan seorang pemain akan menerima kartu pertama dengan nilai 10 adalah 16/52. Peluang pemain mendapatkan kartu As setelah itu adalah 4/51. Setelah dikalikan, kita mendapatkan 16/663.
Jika kita ingin mengetahui probabilitas mendapatkan blackjack, kita hanya perlu menambahkan kedua fenomena ini. Jadi, 16/663 + 16/663 = 32/663 = 4,827%. Dengan kata lain, seorang pemain mendapatkan blackjack setiap 20 tangan sekali. Anda dapat menghitung probabilitas untuk tabel multi-dek dengan cara yang sama, yang telah kami lakukan untuk Anda.
|
Jumlah paket |
Probabilitas |
|
1 |
4,827 % |
|
2 |
4,780 % |
|
3 |
4,764 % |
|
4 |
4,757 % |
|
5 |
4,752 % |
|
6 |
4,749 % |
Probabilitas untuk payudara
Mungkin juga menarik untuk mengetahui berapa peluang Anda untuk gagal. Sekali lagi, kami akan fokus pada contoh situasi di mana Anda bermain hanya dengan dealer di meja dek tunggal. Mari kita lihat situasi yang sangat sederhana di mana seorang pemain memiliki 2 kartu dengan nilai total 10 sehingga dia memiliki 20 poin. Dalam situasi di mana pemain mendapatkan kartu ketiga, 3 kartu telah dimainkan dari dek. Ini menyisakan 49 kartu di dek. Dari 49 kartu ini, hanya 4 kartu As yang akan membantu Anda. Dari 49 kartu ini, 45 kartu tidak diinginkan. Oleh karena itu, peluang kegagalannya adalah 45/49 = 0,9183673.
Anda bisa menghitung probabilitas lain dengan cara yang sama. Anda harus selalu bisa membayangkan situasi dengan benar. Itu saja.
|
Nilai tangan |
Probabilitas payudara |
|
21 |
100 % |
|
20 |
92 % |
|
19 |
85 % |
|
18 |
77 % |
|
17 |
69 % |
|
16 |
62 % |
|
15 |
58 % |
|
14 |
56 % |
|
13 |
39 % |
|
12 |
31 % |
|
11 kurang |
0 % |
Selanjutnya mari kita lihat seberapa besar kemungkinan dealer akan menggertak untuk setiap kartu.
|
Nilai tangan |
Probabilitas payudara |
|
2 |
35,30 % |
|
3 |
37,56 % |
|
4 |
40,28 % |
|
5 |
42,89 % |
|
6 |
42,08 % |
|
7 |
25,99 % |
|
8 |
23,86 % |
|
9 |
23,34 % |
|
10, J, Q, K |
21,43 % |
|
Ace |
11,65 % |
Probabilitas poker
Poker adalah permainan kartu lain yang sangat penting dalam hal probabilitas. Di antara hal-hal lainnya. Jadi mari kita lihat peluang Anda di poker.
Probabilitas pra-flop
Setelah kita menguraikan bagaimana probabilitas bekerja dalam setumpuk kartu, mari kita masuk ke aplikasi praktis. Pertama-tama, kami akan menunjukkan kepada Anda cara menghitung probabilitas kehabisan pasangan (misalnya, kartu As yang banyak dibicarakan). Dalam hal ini, kita perlu mengalikan probabilitas satu sama lain.
(4/52) x (3/51) = (12/2652) = (1/221) = 0,004524 (0,45 %)
📌 Catatan: Jika Anda bermain poker di kasino yang menangani sekitar 30 kartu per jam, Anda akan mendapatkan sepasang kartu As setiap 7,5 jam sekali.
Jadi, berapa peluang mendapatkan salah satu dari 13 pasangan yang mungkin saat Anda bertransaksi? Kita dapat mengasumsikan bahwa peluangnya adalah 1/221 per pasangan (lihat rumus di atas). Total ada 13 pasangan ini, jadi rumus perhitungannya adalah 13/221 = 0,0588. Jadi Anda dapat mengharapkan sepasang setiap 35 pertandingan.
Probabilitas dalam pemain poker melawan pemain
Namun, poker adalah permainan multipemain, biasanya dimainkan melawan satu sama lain. Jadi, inilah pilihan situasi pre-flop yang paling umum.
|
Tanganmu. |
Tangan lawan Anda |
Kemungkinan menang |
|
Pasangan tinggi |
Dua kartu rendah |
83 % |
|
Pasangan tinggi |
Pasangan rendah |
82 % |
|
Pasangan tengah |
Kartu tinggi, kartu rendah |
71 % |
|
Dua kartu tinggi |
Dua kartu rendah |
63 % |
|
Dua kartu tinggi |
Pasangan rendah |
55 % |
Perhitungan probabilitas dengan "out"
Jika Anda berhasil melihat kartu di flop, Anda pasti akan lebih tertarik pada peluang Anda untuk meningkatkan kartu Anda. Dalam hal ini, kita akan membicarakan tentang apa yang disebut "out". Dalam poker, istilah ini mengacu pada kartu apa pun yang dapat membantu Anda. Kasus yang umum terjadi adalah ketika seorang pemain memegang dua kartu dalam satu setelan dan dua kartu lagi dari setelan yang sama muncul di flop. Pemain kemudian memiliki 4 kartu untuk disiram dan dengan demikian memiliki 9 out, menyisakan 9 kartu yang dapat digunakan untuk membentuk flush.
|
Jumlah keluar |
Gagal - Belok |
Belok - Sungai |
Putar Sungai |
|
20 |
42,6 % |
43,5 % |
67,5 % |
|
19 |
40,4 % |
41,3 % |
65,0 % |
|
18 |
38,3 % |
39,1 % |
62,4 % |
|
17 |
36,2 % |
37,0 % |
59,8 % |
|
16 |
34,0 % |
34,8 % |
57,0 % |
|
15 |
31,9 % |
32,6 % |
54,1 % |
|
14 |
29,8 % |
30,4 % |
51,2 % |
|
13 |
27,7 % |
28,3 % |
48,1 % |
|
12 |
25,5 % |
26,1 % |
45,0 % |
|
11 |
23,4 % |
23,9 % |
41,7 % |
|
10 |
21,3 % |
21,7 % |
38,4 % |
|
9 |
19,1 % |
19,6 % |
35,0 % |
|
8 |
17,0 % |
17,4 % |
31,5 % |
|
7 |
14,9 % |
15,2 % |
27,8 % |
|
6 |
12,8 % |
13,0 % |
24,1 % |
|
5 |
10,6 % |
10,9 % |
20,3 % |
|
4 |
8,5 % |
8,7 % |
16,5 % |
|
3 |
6,4 % |
6,5 % |
12,5 % |
|
2 |
4,3 % |
4,3 % |
8,4 % |
|
1 |
2,1 % |
2,2 % |
4,3 % |
📌 Catatan: Ada metode yang sangat mudah untuk menghitung probabilitas out, sehingga Anda dapat melakukannya langsung di meja. Hal ini umumnya disebut aturan "empat dan dua". Setelah kegagalan, pemain cukup mengalikan jumlah kegagalan dengan 4 untuk menemukan probabilitas untuk giliran dan sungai. Jika dia tidak mendapatkan kartu pada gilirannya, dia cukup mengalikan jumlah out dengan dua untuk mendapatkan perkiraan probabilitas mendapatkan kartu di sungai.
Sekali lagi, kita dapat menggunakan contoh memiliki 4 kartu dengan jenis yang sama setelah kegagalan. Jadi, out Anda adalah 9 kartu dan kemungkinan flush setelah giliran dan sungai adalah 36% (9x4). Katakanlah Anda tidak mendapatkan kartu pada gilirannya. Dalam hal ini, kita kemudian mengalikan out dengan dua dan menemukan bahwa kita memiliki peluang 18% (9x2) untuk kehabisan kartu dalam setelan di sungai. Seperti yang bisa Anda lihat dengan membandingkan tabel, metode ini sangat sederhana, tetapi di sisi lain tidak akurat, namun bisa digunakan.

 ID
ID  English
English  čeština
čeština  Polski
Polski  Slovenčina
Slovenčina  Русский
Русский  Deutsch
Deutsch  Slovenski
Slovenski  Dutch
Dutch  Svenska
Svenska  Português
Português  Italiano
Italiano  Español
Español  Français
Français  Suomalainen
Suomalainen  Български
Български  Românesc
Românesc  Magyar
Magyar  Eesti
Eesti  Ελληνική
Ελληνική  Latviešu
Latviešu  Lietuvių
Lietuvių  やまと
やまと  中国
中国  Dansk
Dansk  Türkçe
Türkçe  Українська
Українська  한국어
한국어  Norsk
Norsk 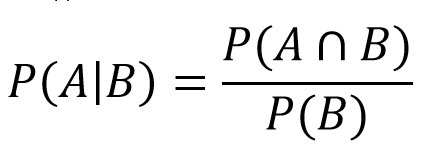


Anda harus masuk untuk menambahkan komentar