Sannsynlighet og kasinospill
 Peter Sommer
Peter Sommer
Forstår du sjansene dine? Hvis du skal spille på et kasino, bør du sørge for at du kjenner sjansene dine og forstår dem perfekt. Hvorfor? Fordi sannsynlighet er motoren som får kasinoer til å fungere. Uten sannsynlighet ville ikke spillindustrien være mulig.
Sjanse er ganske enkelt sannsynligheten for at noe vil skje. Sannsynlighet er en del av hverdagen vår. Når vi bestemmer oss for å krysse en trafikkert gate på rødt lys, er det en viss sjanse for at vi blir påkjørt av en bil, men til gjengjeld har vi en sjanse til å krysse gaten raskere og få litt tid til overs.
Når vi spiller, anslår vi sannsynligheten for at en bestemt hendelse skal inntreffe for å formulere innsatsen vår. Det er i disse tilfellene vi beregner sannsynlighet.
💡 Eksempel på sannsynlighet
La oss si at vi har en pose med fire baller, hvorav bare én er rød og de tre andre er blå. Sannsynligheten for å trekke ut bare den røde ballen uten å se er 1 av 4.
Det er flere måter å uttrykke sannsynlighet på. Vi kan også si at det er en 3 i 1 sjanse mot rødt, fordi vi i gjennomsnitt trekker tre blå baller for hver røde ball som trekkes.
Vi kan også uttrykke sjansene våre i prosent, så sannsynligheten for å trekke en rød ball er 25% hvis det er 100% sjanse for å trekke en ball. Så 100 delt på fire gir oss 25 %.
Sannsynligheten for å trekke en blå ball er 75% hvis det er tre blå baller med 25% sjanse for å trekke.
Sannsynlighet for kasinospill
Kasinoet opererer på prinsippet om å tilby odds som ikke er så gode med tanke på vårt langsiktige resultat.
Eksemplet med en pose ballonger er en enkel måte å vise hvordan et kasino fungerer på. La oss si at et kasino tilbyr odds på 3 for å trekke en rød ball. Hvis du satser $5, vil du i gjennomsnitt i fire forsøk trekke den blå ballen 3 ganger og tape $15, og den fjerde gangen trekker du den røde ballen og vinner $10, men kasinoet vil fortsatt være i svart med $5.
All gambling handler bare om sannsynlighet. Enhver erfaren gambler
vil fortelle deg det. Det er derfor viktig å være kjent med disse tallene og vite hvordan man arbeider med dem. Så her vil vi nå vise deg hvordan du beregner sannsynligheten i pengespill. Hvis du forstår prinsippet riktig, kan du bruke det til å beregne sannsynligheten for noe annet.
Sannsynlighet ved rulett
Rulett er som lykkehjulet. Og vet du hvorfor? Det tar bare 3 ord å forklare - Big Number Theory. Hver person som driver et kasino eller produserer online kasinospill kjenner denne teorien veldig godt. Fordi det er direkte knyttet til inntektene hans. Og takket være det vinner kasinoet alltid over spillerne i det lange løp også. Alt er knyttet til sannsynlighet og husets fordel.
Merk: Alle tallene i artikkelen refererer til European Roulette - så vi teller 37 tall.
Hvordan skrive sannsynlighet
Det er flere måter å skrive sannsynlighet på. Det mest kjente er sannsynligvis prosenter. I tillegg til disse brukes uttrykk som bruker en brøk eller et forholdstall.
- Uttrykt i prosent (%) - ikke mye å legge til her, men for fullstendighetens skyld er dette prosentandelen for den valgte hendelsen. Det beregnes som (Del/Totalt)*100. For eksempel er sannsynligheten for å treffe det valgte tallet på et ruletthjul (Straight): 1/37*100 = 2,7 %.
- Uttrykk ved hjelp av brøker (1/x) - Når vi uttrykker sannsynlighet ved hjelp av en brøk, sier vi at fenomenet forekommer 1 gang av X forsøk. I det numeriske uttrykket er vi avhengige av å beregne prosentandeler. Hvis vi ser på eksemplet 1/37 ovenfor, betyr dette at et statistisk valgt tall på ruletthjulet vil falle 1 gang på 37 spinn.
- Uttrykk etter forhold (x til 1) - Hver gang X inntreffer, skjer det valgte fenomenet 1 gang. Også her holder vi oss til sannsynligheten for det valgte nummeret på rulett. I dette tilfellet vil forholdet skrives som 36 til 1. Dette betyr at etter hvert 36 spinn der tallet ikke faller, vil det være ett tilfelle der det valgte tallet faller.
Merk: Som teorien om store tall sier, er sannsynlighet i hovedsak en matematisk grense. Med flere og flere forsøk kommer du realistisk sett nærmere og nærmere det beregnede resultatet.
Som du kan se, er uttrykkene ved bruk av brøk og ved bruk av forholdstall svært like. Den eneste forskjellen er at en brøk teller alle spinn, mens en ratio deler det totale antallet spinn i to kategorier.
Tabell over sannsynligheter for individuelle spill i rulett
|
Innsats |
Utdrag fra |
Forhold |
Prosentandeler |
|
En rett innsats |
1/2,055 |
1,055 til 1 |
48,6 % |
|
Spalte |
1/3,08 |
2,08 til 1 |
32,4 % |
|
The Dozen |
1/3,08 |
2,08 til 1 |
32,4 % |
|
Seks linjer |
1/6,17 |
5,17 til 1 |
16,2 % |
|
Hjørne |
1/9,25 |
8,25 til 1 |
10,8 % |
|
Gate |
1/12,33 |
11,33 til 1 |
8,1 % |
|
Split |
1/19,5 |
18,5 til 1 |
5,4 % |
|
Rett |
1/37 |
36 mot 1 |
2,7 % |
Sannsynlighet for en rett innsats
En matematisk sammenligning for gjentakelse av det valgte fenomenet kan også være interessant. For dette tilfellet har vi valgt et rett spill, spesifikt for eksempel et spill på rødt. Så, hva vil være den endrede sannsynligheten for rødt 5 ganger på rad, for eksempel?
|
Antall spinn |
Forhold |
Prosentandeler |
|
1 |
1,06 til 1 |
48,6 % |
|
2 |
3,23 til 1 |
23,7 % |
|
3 |
7,69 til 1 |
11,5 % |
|
4 |
16,9 til 1 |
5,6 % |
|
5 |
35,7 til 1 |
2,73 % |
|
6 |
74,4 til 1 |
1,33 % |
|
7 |
154 til 1 |
0,65 % |
|
8 |
318 til 1 |
0,31 % |
|
9 |
654 til 1 |
0,15 % |
|
10 |
1 346 til 1 |
0,074 % |
|
15 |
49 423 til 1 |
0,002 % |
|
20 |
1 813 778 til 1 |
0,000055 % |
Som man kan se, reduseres sannsynligheten for dette fenomenet raskt etter hvert som antall spinn øker. Husk imidlertid at disse sannsynlighetene beskriver fenomenet som helhet. Den tilfeldige tallgeneratoren tar ikke hensyn til tidligere resultater, så selv om en spillserie der rødt treffer 20 ganger på rad forekommer en gang hver 1,813 millioner spill, vil en runde med 21 spill ha samme husfordel og sannsynlighet (dvs. 48,6%) som alle andre spillrunder.
Ofte i dette tilfellet kan man støte på begrepet Player's Fallacy, der spilleren tror at hvis en farge blir truffet flere ganger på rad, er det større sannsynlighet for at den andre fargen vil bli truffet i neste spinn. I virkeligheten er dette ikke tilfelle. Det mest berømte tilfellet av denne feilslutningen ble observert i 1913 på Monte Carlo Casino, da svart falt 26 ganger på rad på ruletthjulet, og i nesten hele denne utrolige streken, og selv etter at den ble avsluttet, satset folk frenetisk på rødt. Det var da kasinoet tjente veldig gode penger.
Merk: Sannsynligheten for at en farge blir truffet 26 ganger på rad er 0,000000730870% og forekommer en gang i 67 millioner spill.
Hvordan beregne sannsynligheten for rulett
Vil du vite flere odds for individuelle spill? Prøv å beregne dem selv. Å arbeide med prosenter og sannsynligheter er ikke veldig komplisert. Vanligvis er det enklest å starte med brøker og bruke dem til å beregne ytterligere prosenter og forholdstall. Hvis du for eksempel vil beregne sannsynligheten i en brøk for en situasjon der rødt er rødt, gjør du følgende:
Totalt antall røde på spillefeltet/Totalt antall spillefelt = 18/37
Sannsynlighet for ett spinn
Også her gjelder en enkel regel. Bare regn ut antall felter som gir deg gevinst og del det på det totale antallet felter.
For eksempel:
- Farge - 18/37
- Sudá/Lichá - 18/37
- Dusin - 12/37
- Antall 0 - 1/37
- Svart og partall - 9/37 (det er bare 9 tall i spillefeltet som er både svarte og partall)
- Dusin og kolonne - 4/37 (det er bare 4 tall i et dusin og i en kolonne)
Akkurat som sannsynligheten for å vinne, kan du beregne sannsynligheten for å tape. Bare tell antall ikke-vinnende felt og del dem igjen med det totale antallet felt. For eksempel er sannsynligheten for å tape hvis du satser på rødt 19/37 (18 svarte felt + grønn null).
Merk: For å redusere en brøk til 1/x dividerer du bare telleren og nevneren med telleren. For eksempel blir 18/37 (du deler begge tallene på 18) 1/2,055 etter justeringen. Og så betyr dette at for hver 2,055 omdreining vil en omdreining resultere i en rød eller en svart.
Sannsynlighet for flere spinn
Når du har mestret beregningen for enkeltspinn, er det veldig enkelt å beregne sannsynligheten for flere spinn. Bare multipliser de enkelte brøkene med hverandre.
Eksempler:
- spinn - spill på rødt = 18/37
- spinn - innsats per dusin = 12/37
Sannsynlighet for å vinne begge rundene = (18/37)*(12/37)=1/6,34 eller 15,77 % eller 5,34 til 1.
- spinn - rett innsats - 1/37
- spinn - rett innsats - 1/37
Sannsynlighet for å vinne begge rundene = (1/37)*(1*37)=1/1369 eller 0,073% eller 1368 til 1
- spinn - satse på svart og oddetall 9/37
- spinn - satse på jevn 18/37
- spinn - kolonneinnsats 12/37
Sannsynlighet for å vinne alle 3 runder = (9/37)*(18/37)*(12/37)=1/26,06 eller 3,84 % eller 25,06 til 1.
Selve konverteringen mellom oppføringene er igjen svært enkel. Du får prosentandelen ved å dele brøken på formen 1/x og deretter multiplisere med 100. Du får den proporsjonale notasjonen i form av X til 1 ved å trekke 1 fra nevneren, som er den vinnende runden av totalen. Se eksempler over avsnittet.
Sannsynlighet for terninger
Craps er et annet sjansespill der det er relativt enkelt å beregne oddsen. Før vi begynner å beregne oddsen for å vinne på craps, la oss ta en titt på sannsynligheten for terningkast i seg selv.
Terningen har 6 sider. Sjansen for at et tall vil falle er derfor 1/6. Craps spilles tradisjonelt med to terninger. Oddsen for at to tall kombineres er derfor 2/36. Vi er imidlertid ikke så mye interessert i de spesifikke tallene som summen av disse tallene, som er mye viktigere i craps. Igjen bruker vi formelen: antall vinnerkombinasjoner / antall av alle kombinasjoner.
La oss si at vi ønsker å vite sannsynligheten for summen 7. Vinnende kombinasjoner: (1-6), (2-4), (3-3), (4-2), (6-1). Som du kan se, er det totalt 6 forskjellige kombinasjoner der summen 7 kan kastes på to terninger. Og siden antallet av alle kombinasjoner er 36, er sannsynligheten for 7 6/36 = 0,1666.
På denne måten kan alle andre mulige resultater enkelt beregnes.
|
Totalt |
Sannsynlighet |
|
2 |
1/36 |
|
3 |
2/36 |
|
4 |
3/36 |
|
5 |
4/36 |
|
6 |
5/36 |
|
7 |
6/36 |
|
8 |
5/36 |
|
9 |
4/36 |
|
10 |
3/36 |
|
11 |
2/36 |
|
12 |
1/36 |
Oddsen for å vinne på craps
La oss kort ta en titt på terningreglene. Den vanligste innsatsen er Pass Line.
- Hvis du kaster en 7 eller 11, vinner du
- Hvis du kaster en 2, 3 eller 12, taper du
- I andre tilfeller (4, 5, 6, 8, 9 eller 10) bestemmes et poeng og kastes til dette poenget kastes igjen (vinn) eller en 7 kastes (tap).
Vi beregner først sannsynligheten for å vinne før vi bestemmer poenget. Sjansen for å treffe 7 er 6/36 og sjansen for å treffe 11 er 2/36. Disse to brøkene må deretter legges sammen for å gi 3/36+2/36 = 2/9 = 0,2222.
Vi retter nå oppmerksomheten mot situasjonen der et punkt er bestemt. Det vil si når punktet er 4, 5, 6, 8, 9 eller 10. La oss starte med totalt 4.
Hvis en 4 kastes, bestemmes et poeng, og spilleren kaster til en 4 eller 7 kastes. Det er her vi kommer inn i området for betinget sannsynlighet. Dette forteller oss hva sannsynligheten for hendelse A er hvis hendelse B inntreffer samtidig. I vårt tilfelle vil det være hva sannsynligheten for at vi vinner (ruller en 4) hvis runden slutter (ruller en 4 eller en 7). Deretter setter vi disse verdiene inn i formelen:
- P(A) = faller summen av 4: 3/36
- P(A∩B) = etter justeringer finner vi at den er lik A
- P(B) = Fall 4 eller 7: 3/36 + 6/36 = 9/36
Det følger av dette:
- P(4|4 eller 7) = (3/36)/(9/36) = 1/3
På lignende måte kan vi beregne summene av 5, 6, 8, 9 og 10
- P(5|5 eller 7) = (4/36)/(10/36) = 2/5
- P(6|6 eller 7) = (5/36)/(11/36) = 5/11
- P(8|8 eller 7) = (5/36)/(11/36) = 5/11
- P(9|9 eller 7) = (4/36)/(10/36) = 2/5
- P(10|10 eller 7) = (3/36)/(9/36) = 1/3
Nå kan vi beregne sjansen for å vinne som sannsynligheten for det opprinnelige kastet da poenget ble bestemt og neste kast da spilleren vant.
- Opprinnelig roll 4 x P(4|4 eller 7) = 3/36 x 1/3 = 1/36
- Opprinnelig rull 5 x P(5|5 eller 7) = 4/36 x 2/5 = 2/45
- Opprinnelig rull 6 x P(6|6 eller 7) = 5/36 x 5/11 = 25/396
- Opprinnelig rull 8 x P(8|8 eller 7) = 5/36 x 5/11 = 25/396
- Originalrull 9 x P(9|9 eller 7) = 4/36 x 2/5 = 2/45
- Opprinnelig rull 10 x P(10|10 eller 7) = 3/36 x 1/3 = 1/36
Alle disse brøkene gir oss sannsynligheten for å vinne hvis det første kastet er 4, 5, 6, 8, 9 eller 10. Hvis du vil vite den totale sannsynligheten for å vinne på et Pass line-spill, må du legge dem alle sammen og legge til sjansen for å vinne før poenget (kaster en 7 eller 11 - 2/9).
2/9 + 1/36 + 2/45 + 25/396 + 25/396 + 2/45 + 1/36 = 244/495
Fordi 244/495 er nøyaktig 49,3 %. Det er i underkant av 50 %. Faktisk vil du sannsynligvis ikke finne en bedre sjanse til å vinne med en 1 i 1 utbetaling. Bortsett fra kanskje blackjack, hvis du kan telle kort.
Sannsynlighet for blackjack
Blackjack er sjansespillet der oddsen betyr mest. I blackjack kan du påvirke husets fordel med din dyktighet og kunnskap. Du trenger bare å vite den optimale strategien for dette, og hvis du vet hvordan du teller kort, vil du til og med spille med spillerens fordel. Rundt og rundt trenger du faktisk ikke å vite alle de spesifikke sannsynlighetene, fordi alle disse beregningene allerede er gjort av matematikere før deg som kom med alle taktikker og strategier for blackjack.
Av hensyn til interessen vil vi imidlertid vise hvordan du beregner sannsynligheten for noen viktige fenomener i blackjack.
Hvis vi ser på sannsynlighetsproblemet fra perspektivet til en kortstokk, er det klart at antallet mulige utfall øker raskt. Blackjack spilles med en kortstokk med 52 kort, 4 farger og 13 verdier. Dette gir følgende odds:
- Jeg trekker et ess fra kortstokken (eller et hvilket som helst individuelt kort): 4/52=0.0769 (7.69%)
- Jeg trekker en spade fra kortstokken: 13/52=0.25 (25%)
Men i motsetning til for eksempel myntkast, rulett eller spilleautomater, har en kortstokk et slags "minne". Eller rettere sagt, det betyr at tidligere resultater påvirker nåværende og fremtidige tiltak. Dette skyldes at et kort har falt fra kortstokken, og dette endrer utgangssituasjonen. La oss se på et eksempel der et ess ble trukket som det første kortet fra en kortstokk med 52 kort (7,69% sjanse). Sannsynligheten for at et ess trekkes igjen som det andre kortet fra kortstokken vil nå være annerledes. Etter den første trekningen har antall ess falt til 3 og antall kort til 51.
Sannsynlighet for blackjack naturlig
Det hver spiller vil være interessert i først er sannsynligheten for blackjack. Det vil si hva er sjansene for at en spiller får et ess og et ti-kort rett i begynnelsen av runden - med andre ord en naturlig.
Denne situasjonen kan oppstå på to måter, og hvis vi legger til de to måtene, får vi oddsen vår på blackjack:
Merk: Vi teller for single deck blackjack. Så 52 kort, 4 ess og 16 tiere. Dealerens kort er ikke synlig, så det vil ikke påvirke sannsynligheten.
- Spilleren mottar det første esset og et ti-kort.
Spilleren får utdelt det første ess-kortet med 4/52 sannsynlighet. Så spilleren må få det andre kortet med en tier, og for det er oddsen 16/51. Disse to sannsynlighetene må multipliseres sammen for å få 16/663.
- Spilleren mottar det første ti kortet og et ess.
Sannsynligheten for at en spiller får det første kortet med verdien 10 er 16/52. Oddsen for at en spiller får et ess etter det er 4/51. Etter å ha multiplisert får vi 16/663.
Hvis vi vil vite sannsynligheten for å få en blackjack, legger vi bare til disse to fenomenene. Så 16/663 + 16/663 = 32/663 = 4,827 %. Med andre ord, en spiller får en blackjack omtrent hver 20. hånd. Du kan beregne sannsynligheten for tabeller med flere dekk på en lignende måte, noe vi allerede har gjort for deg.
|
Antall pakker |
Sannsynlighet |
|
1 |
4,827 % |
|
2 |
4,780 % |
|
3 |
4,764 % |
|
4 |
4,757 % |
|
5 |
4,752 % |
|
6 |
4,749 % |
Sannsynlighet for bust
Det kan også være interessant å vite hva oddsen din er for en byste. Igjen vil vi fokusere på en eksempelsituasjon der du spiller med bare dealeren ved et enkelt kortbord. La oss ta en titt på en veldig enkel situasjon der en spiller har 2 kort med en verdi på 10 totalt, slik at han har 20 poeng. I en situasjon der spilleren får et tredje kort, har 3 kort allerede blitt spilt fra kortstokken. Dette etterlater 49 kort i kortstokken. Av disse 49 kortene vil bare 4 ess hjelpe deg. Av disse 49 kortene er 45 uønskede. Derfor er oddsen for en byste 45/49 = 0,9183673.
Du kan beregne andre sannsynligheter på lignende måte. Du må alltid være i stand til å forestille deg situasjonen riktig. Det er alt.
|
Verdien av hånden |
Sannsynlighet for arrestasjoner |
|
21 |
100 % |
|
20 |
92 % |
|
19 |
85 % |
|
18 |
77 % |
|
17 |
69 % |
|
16 |
62 % |
|
15 |
58 % |
|
14 |
56 % |
|
13 |
39 % |
|
12 |
31 % |
|
11 mindre |
0 % |
La oss deretter se på hvor sannsynlig dealeren vil byste for hvert kort.
|
Verdien av hånden |
Sannsynlighet for arrestasjoner |
|
2 |
35,30 % |
|
3 |
37,56 % |
|
4 |
40,28 % |
|
5 |
42,89 % |
|
6 |
42,08 % |
|
7 |
25,99 % |
|
8 |
23,86 % |
|
9 |
23,34 % |
|
10, J, Q, K |
21,43 % |
|
Ess |
11,65 % |
Sannsynlighet for poker
Poker er et annet kortspill der sannsynlighet er ekstremt viktig. Blant annet. Så la oss ta en titt på hva sjansene dine er i poker.
Sannsynlighet før flopp
Nå som vi har skissert hvordan sannsynlighet fungerer i en kortstokk, la oss komme til praktiske anvendelser. Først og fremst viser vi deg hvordan du beregner sannsynligheten for å gå tom for et par (for eksempel de mye omtalte essene). I dette tilfellet må vi multiplisere sannsynlighetene med hverandre.
(4/52) x (3/51) = (12/2652) = (1/221) = 0,004524 (0,45 %)
Merk: Hvis du spiller poker i et kasino som gir omtrent 30 hender i timen, vil du få et par ess omtrent en gang hver 7 og en halv times spill.
Så hva er sjansene for å få noen av de 13 mulige parene når du gir? Vi kan anta at oddsen er 1/221 per individuelt par (se formelen ovenfor). Det kan være 13 av disse parene totalt, så formelen for beregningen blir 13/221 = 0,0588. Så du kan forvente et par omtrent hver 35. kamp.
Sannsynlighet i poker spiller mot spiller
Poker er imidlertid et flerspillerspill, vanligvis spilt mot hverandre. Så her er et utvalg av de vanligste pre-flop-situasjonene.
|
Din hånd |
Motstanderens hånd |
Sannsynlighet for å vinne |
|
Høyt par |
To lave kort |
83 % |
|
Høyt par |
Lavt par |
82 % |
|
Midterste par |
Høyt, lavt kort |
71 % |
|
To høye kort |
To lave kort |
63 % |
|
To høye kort |
Lavt par |
55 % |
Beregning av sannsynlighet etter "outs"
Hvis du klarer å se kortene på floppen, vil du absolutt være ytterligere interessert i hva sjansene dine er for å forbedre hånden din. I dette tilfellet vil vi snakke om de såkalte "outs". I poker refererer dette begrepet til alle kort som kan hjelpe deg. Et slikt vanlig tilfelle kan være når en spiller har to kort i en farge og to kort til i samme farge vises på floppen. Spilleren har da 4 kort å flushe og har dermed 9 outs, og etterlater 9 kort å danne en flush med.
|
Antall uteblivelser |
Flop - Turn |
Sving - Elv |
Snu en elv |
|
20 |
42,6 % |
43,5 % |
67,5 % |
|
19 |
40,4 % |
41,3 % |
65,0 % |
|
18 |
38,3 % |
39,1 % |
62,4 % |
|
17 |
36,2 % |
37,0 % |
59,8 % |
|
16 |
34,0 % |
34,8 % |
57,0 % |
|
15 |
31,9 % |
32,6 % |
54,1 % |
|
14 |
29,8 % |
30,4 % |
51,2 % |
|
13 |
27,7 % |
28,3 % |
48,1 % |
|
12 |
25,5 % |
26,1 % |
45,0 % |
|
11 |
23,4 % |
23,9 % |
41,7 % |
|
10 |
21,3 % |
21,7 % |
38,4 % |
|
9 |
19,1 % |
19,6 % |
35,0 % |
|
8 |
17,0 % |
17,4 % |
31,5 % |
|
7 |
14,9 % |
15,2 % |
27,8 % |
|
6 |
12,8 % |
13,0 % |
24,1 % |
|
5 |
10,6 % |
10,9 % |
20,3 % |
|
4 |
8,5 % |
8,7 % |
16,5 % |
|
3 |
6,4 % |
6,5 % |
12,5 % |
|
2 |
4,3 % |
4,3 % |
8,4 % |
|
1 |
2,1 % |
2,2 % |
4,3 % |
Merk: Det er en veldig enkel metode for å beregne sannsynligheten for outs, slik at du kan gjøre det rett ved bordet. Det kalles vanligvis "fire og to"-regelen. Etter floppen multipliserer spilleren ganske enkelt antall outs med 4 for å finne sannsynligheten for turn og river. Hvis han ikke får kortet på turn, multipliserer han ganske enkelt antall outs med to for å få den omtrentlige sannsynligheten for å få kortet på river.
Igjen kan vi bruke eksemplet med å ha 4 kort i samme farge etter floppen. Så dine outs er 9 kort og sannsynligheten for en flush etter turn og river er 36% (9x4). La oss si at du ikke får et kort på turen. I det tilfellet multipliserer vi deretter outs med to og finner ut at vi har 18% (9x2) sjanse for å gå tom for kort i fargen på river. Som du kan se ved å sammenligne tabellen, er denne metoden veldig enkel, men på den annen side unøyaktig, men den kan brukes.

 NO
NO  English
English  čeština
čeština  Polski
Polski  Slovenčina
Slovenčina  Русский
Русский  Deutsch
Deutsch  Slovenski
Slovenski  Dutch
Dutch  Svenska
Svenska  Português
Português  Italiano
Italiano  Español
Español  Français
Français  Suomalainen
Suomalainen  Български
Български  Românesc
Românesc  Magyar
Magyar  Eesti
Eesti  Ελληνική
Ελληνική  Latviešu
Latviešu  Lietuvių
Lietuvių  やまと
やまと  中国
中国  Dansk
Dansk  Türkçe
Türkçe  ID
ID  Українська
Українська  한국어
한국어 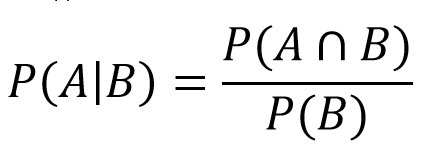


Du må være innlogget for å legge til en kommentar.