Tõenäosus ja kasiinomängud
 Peter Sommer
Peter Sommer
Kas sa mõistad oma võimalusi? Kui sa kavatsed kasiinos mängida, peaksid sa olema kindel, et sa tead oma võimalusi ja mõistad neid suurepäraselt. Miks? Sest tõenäosus on mootor, mis paneb kasiinod tööle. Ilma tõenäosuseta ei oleks hasartmängutööstus võimalik.
Juhus on lihtsalt tõenäosus, et midagi juhtub. Tõenäosus on osa meie igapäevaelust. Kui me otsustame ületada tiheda liiklusega tänava punase tulega, on olemas teatud võimalus, et meid tabab auto, kuid vastutasuks on meil võimalus ületada tänav kiiremini ja võita veidi aega.
Kui me mängime, siis hindame teatud sündmuse toimumise tõenäosust, et sõnastada oma panus. Sellistel juhtudel arvutame tõenäosust.
💡 Tõenäosuse näide
Oletame, et meil on kott, mis sisaldab nelja palli, millest ainult üks on punane ja ülejäänud kolm on sinised. Tõenäosus tõmmata välja ainult punane pall ilma vaatamata on 1:4.
Tõenäosust saab väljendada mitmel viisil. Võime ka öelda, et punase vastu on tõenäosus 3:1, sest keskmiselt loosime iga punase palli kohta kolm sinist palli.
Me võime väljendada oma võimalusi ka protsentides, nii et meie tõenäosus tõmmata punane pall on 25%, kui on 100% tõenäosus tõmmata pall. Seega 100 jagatud neljaga annab 25%.
Sinise palli tõmbamise tõenäosus on 75%, kui on kolm sinist palli, mille tõmbamise tõenäosus on 25%.
Kasiinomängude tõenäosus
Kasiino tegutseb põhimõttel, et pakub koefitsiente, mis ei ole meie pikaajalist tulemust arvestades nii head.
Näide õhupallide kotist on lihtne viis näidata, kuidas kasiino töötab. Oletame, et kasiino pakub punase palli loosimiseks koefitsienti 3. Kui panustate 5 dollarit, siis nelja katse jooksul tõmbate sinist palli keskmiselt kolm korda ja kaotate 15 dollarit, neljandal korral tõmbate punast palli ja võidate 10 dollarit, kuid kasiino jääb ikkagi 5 dollariga miinusesse.
Kõik hasartmängud on lihtsalt tõenäosus. Iga kogenud mängur
ütleb teile seda. Seetõttu on oluline neid numbreid tunda ja osata nendega töötada. Nii et siinkohal näitame teile nüüd, kuidas arvutada tõenäosust hasartmängude puhul. Kui te mõistate seda põhimõtet õigesti, saate seda kasutada millegi muu tõenäosuse arvutamiseks.
Tõenäosus ruletis
Rulett on nagu õnneratas. Ja teate, miks? Selgitamiseks kulub vaid 3 sõna - Suure numbri teooria. Iga inimene, kes juhib kasiinot või toodab online kasiinomänge, teab seda teooriat väga hästi. Sest see on otseselt seotud tema sissetulekuga. Ja tänu sellele võidab kasiino alati ka pikemas perspektiivis panustajate üle. Kõik on seotud tõenäosuse ja maja servaga.
📌 Märkus: Kõik artiklis toodud numbrid viitavad Euroopa ruletile - seega loeme 37 numbrit.
Kuidas kirjutada tõenäosust
Tõenäosuse kirjutamiseks on mitu võimalust. Ilmselt on kõige tuntumad protsendid. Lisaks neile kasutatakse ka väljendeid, milles kasutatakse murdosa või suhtarvu.
- Väljendatud protsentides (%) - siin ei ole palju lisada, kuid lihtsalt täielikkuse huvides on see valitud sündmuse protsent. See arvutatakse järgmiselt: (osa/summa)*100. Näiteks tõenäosus tabada valitud number ruletiratast (sirge): 1/37*100=2,7%.
- Väljendamine murdude abil (1/x) - Kui väljendame tõenäosust murdude abil, ütleme, et nähtus esineb 1 kord X katsest. Numbrilises väljenduses tugineme protsentide arvutamisele. Kui vaatleme eespool toodud 1/37 näidet, tähendab see, et statistiliselt valitud number ruletiratast langeb 1 kord 37 keerutuse jooksul.
- Väljendus suhtarvuga (x ja 1) - Iga kord, kui X esineb, juhtub valitud nähtus 1 kord. Ka siinkohal jääme jälle kinni valitud numbri tõenäosusest ruletis. Sellisel juhul kirjutatakse suhe 36:1. See tähendab, et pärast iga 36 keerutust, kus number ei lange, tuleb üks kord, kus valitud number langeb.
📌 Märkus: Nagu suurarvuteooria ütleb, on tõenäosus sisuliselt matemaatiline piirarv. Üha enamate katsete abil jõuate reaalselt üha lähemale arvutatud tulemusele.
Nagu näete, on murdude ja suhtarvude kasutamine väga sarnane. Ainus erinevus seisneb selles, et fraktsioon loeb kõiki keerutusi, samas kui suhe jagab kõik keerutused kahte kategooriasse.
Ruleti üksikute panuste tõenäosuste tabel
|
Panus |
Väljavõte allikast |
Suhtarv |
Protsendid |
|
Otsene panus |
1/2,055 |
1,055 kuni 1 |
48,6 % |
|
Veerg |
1/3,08 |
2,08-1 |
32,4 % |
|
Dozen |
1/3,08 |
2,08-1 |
32,4 % |
|
Kuus rida |
1/6,17 |
5,17-1 |
16,2 % |
|
Nurgas |
1/9,25 |
8,25:1 |
10,8 % |
|
Street |
1/12,33 |
11,33-1 |
8,1 % |
|
Jagatud |
1/19,5 |
18,5:1 |
5,4 % |
|
Sirge |
1/37 |
36 kuni 1 |
2,7 % |
Tõenäosus sirge panuse puhul
Huvitav võiks olla ka matemaatiline võrdlus valitud nähtuse kordumise kohta. Sel juhul oleme valinud sirge panuse, täpsemalt näiteks panuse punasele. Milline on siis näiteks 5 korda järjest punase värvuse muutumise tõenäosus?
|
Pöörete arv |
Suhtarv |
Protsendid |
|
1 |
1,06 kuni 1 |
48,6 % |
|
2 |
3,23-1 |
23,7 % |
|
3 |
7,69:1 |
11,5 % |
|
4 |
16,9:1 |
5,6 % |
|
5 |
35,7:1 |
2,73 % |
|
6 |
74,4:1 |
1,33 % |
|
7 |
154 kuni 1 |
0,65 % |
|
8 |
318 kuni 1 |
0,31 % |
|
9 |
654-1 |
0,15 % |
|
10 |
1 346 kuni 1 |
0,074 % |
|
15 |
49 423-1 |
0,002 % |
|
20 |
1 813 778 kuni 1 |
0,000055 % |
Nagu näha, väheneb selle nähtuse tõenäosus kiiresti, kui spinnide arv suureneb. Pidage siiski meeles, et need tõenäosused kirjeldavad nähtust tervikuna. Juhuslik numbrigeneraator ei võta arvesse eelnevaid tulemusi, nii et kuigi mänguseeria, kus punane tabab 20 korda järjest, esineb üks kord iga 1,813 miljoni mängu kohta, on 21 mänguvooru puhul sama maja serv ja tõenäosus (st 48,6%) kui iga teise mänguvooru puhul.
Sageli võib sel juhul kohata terminit Player's Fallacy, mille puhul panustaja usub, et kui üks värv tabab mitu korda järjest, on suurem tõenäosus, et järgmisel keerutusel tabab ka teine värv. Tegelikkuses see nii ei ole. Selle eksituse kõige kuulsam juhtum täheldati 1913. aastal Monte Carlo kasiinos, kui ruletiratast tabas 26 korda järjest must, ja peaaegu kogu selle uskumatu seeria jooksul ja isegi pärast selle lõppu panustasid inimesed meeletult punasele. See oli siis, kui kasiino teenis väga kenasti raha.
📌 Märkus: tõenäosus, et ühte värvi tabatakse 26 korda järjest, on 0,000000730870% ja see juhtub üks kord 67 miljonist mängust.
Kuidas arvutada ruleti tõenäosust
Soovite teada rohkem koefitsiente üksikute panuste jaoks? Proovige neid ise välja arvutada. Protsentide ja tõenäosustega töötamine ei ole väga keeruline. Üldiselt on kõige lihtsam alustada murdudest ja kasutada neid edasiste protsentide ja suhtarvude arvutamiseks. Näiteks kui soovite arvutada tõenäosuse murdosa olukorras, kus punane on punane, siis teete järgmist:
Punaste koguarv mänguväljakul / mänguväljakute koguarv = 18/37
Tõenäosus ühe spinni puhul
Ka siin kehtib lihtne reegel. Lihtsalt arvutage välja, kui paljude väljade puhul on teil võimalik võita, ja jagage see väljade koguarvuga.
Näiteks:
- Värv - 18/37
- Sudá/Lichá - 18/37
- Dozen - 12/37
- Number 0 - 1/37
- Must ja paariline - 9/37 (mänguväljal on ainult 9 numbrit, mis on nii mustad kui ka paarilised).
- Tosin ja veerg - 4/37 (tosinas ja veerus on ainult 4 numbrit)
Nii nagu võidutõenäosust, saab ka kaotustõenäosust arvutada. Lihtsalt loendage mittevõitnud väljakute arv ja jagage need uuesti väljakute koguarvuga. Näiteks on punasele panustamise korral kaotamise tõenäosus 19/37 (18 musta väljalanget + roheline null).
📌 Märkus: Murru vähendamiseks 1/x-ks tuleb lihtsalt lugeja ja nimetaja jagada lugejaga. Näiteks 18/37 (jagate mõlemad arvud 18-ga) on pärast korrigeerimist 1/2,055. See tähendab, et iga 2,055 pöörde kohta on üks pöörde tulemuseks punane või must.
Tõenäosus mitme keerutuse korral
Kui olete omandanud ühekordsete keerutuste arvutamise, on mitme keerutuse tõenäosuse arvutamine väga lihtne. Lihtsalt korrutage üksikud murded üksteisega.
Näited:
- spin - panus punasele = 18/37
- spin - panus tosina kohta = 12/37
Tõenäosus võita mõlemad voorud = (18/37)*(12/37)=1/6,34 ehk 15,77% ehk 5,34:1.
- spin - otsene panus - 1/37
- spin - otsene panus - 1/37
Tõenäosus võita mõlemad voorud = (1/37)*(1*37)=1/1369 ehk 0,073% ehk 1368:1.
- spin - panus mustale ja paaritu 9/37
- spinn - panus paarilisele 18/37
- spin - veeru panus 12/37
Tõenäosus võita kõik 3 vooru = (9/37)*(18/37)*(12/37)=1/26,06 ehk 3,84% ehk 25,06:1.
Tegelik konverteerimine kirjete vahel on jällegi väga lihtne. Protsendid saad, kui jagad murdosa kujul 1/x ja seejärel korrutad 100-ga. Proportsionaalse märkimisviisi saate kujul X kuni 1, lahutades nimetajast 1, mis on võidukäik kogusummast. Vt näiteid lõike kohal.
Tõenäosus noppimine
Craps on veel üks õnnemäng, mille puhul on suhteliselt lihtne tõenäosust arvutada. Enne kui me hakkame arvutama täringutega võitmise tõenäosust, vaatleme täringuviskete tõenäosust.
Noppadel on 6 külge. Seega on tõenäosus, et mõni arv langeb, 1/6. Craps'i mängitakse traditsiooniliselt kahe täringuga. Seega on mis tahes kahe numbri kombinatsiooni tõenäosus 2/36. Meid ei huvita aga mitte niivõrd konkreetsed numbrid kui nende arvude summa, mis on crapsis palju olulisem. Jällegi kasutame valemit: võidukombinatsioonide arv/kõigi kombinatsioonide arv.
Oletame, et tahame teada tõenäosust, et summa on 7. Võidud kombinatsioonid: (1-6), (2-4), (3-3), (4-2), (6-1). Nagu näete, on kokku 6 erinevat kombinatsiooni, kus kahe täringuga saab veeretada summa 7. Ja kuna kõikide kombinatsioonide arv on 36, siis on 7 tõenäosus 6/36=0,1666.
Sel viisil saab kõik muud võimalikud tulemused hõlpsasti välja arvutada.
|
Kokku |
Tõenäosus |
|
2 |
1/36 |
|
3 |
2/36 |
|
4 |
3/36 |
|
5 |
4/36 |
|
6 |
5/36 |
|
7 |
6/36 |
|
8 |
5/36 |
|
9 |
4/36 |
|
10 |
3/36 |
|
11 |
2/36 |
|
12 |
1/36 |
Võiduvõimalused crapsis
Vaatame lühidalt täringureegleid. Kõige levinum panus on Pass Line.
- Kui sa viskad 7 või 11, siis sa võidad.
- Kui viskate 2, 3 või 12, kaotate.
- Muudel juhtudel (4, 5, 6, 8, 9 või 10) määratakse punkt ja veeretatakse, kuni see punkt on uuesti veeretatud (võit) või 7 on veeretatud (kaotus).
Enne punkti määramist arvutame kõigepealt võidu tõenäosuse. Tõenäosus tabada 7 on 6/36 ja tõenäosus tabada 11 on 2/36. Need kaks osa tuleb siis liita, et saada 3/36+2/36 = 2/9 = 0,2222.
Nüüd pöörame tähelepanu olukorrale, kus punkt on määratud. See tähendab, et kui punkt on 4, 5, 6, 8, 9 või 10. Alustame kokku 4.
Kui visatakse 4, määratakse punkt ja mängija viskab seni, kuni visatakse 4 või 7. See on koht, kus me siseneme tingimusliku tõenäosuse valdkonda. See ütleb meile, milline on sündmuse A tõenäosus, kui sündmus B toimub samal ajal. Meie puhul on see, mis on tõenäosus, et me võidame (viskab 4), kui voor lõpeb (viskab 4 või 7). Seejärel sisestame need väärtused valemisse:
- P(A) = Falls summa 4: 3/36
- P(A∩B) = pärast kohandusi leiame, et see on võrdne A
- P(B) = 4. või 7. kukkumine: 3/36 + 6/36 = 9/36.
Sellest järeldub, et:
- P(4|4 või 7) = (3/36)/(9/36) = 1/3
Samamoodi saame arvutada 5, 6, 8, 9 ja 10 summad.
- P(5|5 või 7) = (4/36)/(10/36) = 2/5
- P(6|6 või 7) = (5/36)/(11/36) = 5/11
- P(8|8 või 7) = (5/36)/(11/36) = 5/11
- P(9|9 või 7) = (4/36)/(10/36) = 2/5
- P(10|10 või 7) = (3/36)/(9/36) = 1/3
Nüüd saame arvutada võiduvõimaluse kui tõenäosuse, mis tuleneb esialgsest veeretusest, kui punkt määrati, ja järgmisest veeretusest, kui mängija võitis.
- Esialgne viseerimine 4 x P(4|4 või 7) = 3/36 x 1/3 = 1/36
- Esialgne viske 5 x P(5|5 või 7) = 4/36 x 2/5 = 2/45
- Esialgne viske 6 x P(6|6 või 7) = 5/36 x 5/11 = 25/396
- Esialgne viseering 8 x P(8|8 või 7) = 5/36 x 5/11 = 25/396
- Esialgne viskamine 9 x P(9|9 või 7) = 4/36 x 2/5 = 2/45
- Esialgne viseering 10 x P(10|10 või 7) = 3/36 x 1/3 = 1/36
Kõik need murdarvud annavad meile võidu tõenäosuse, kui esimene vise on 4, 5, 6, 8, 9 või 10. Kui soovite teada, kui suur on tõenäosus võita Pass line'i panusega, peate need kõik kokku liita ja lisada võiduvõimaluse enne punkti (viskab 7 või 11 - 2/9).
2/9 + 1/36 + 2/45 + 25/396 + 25/396 + 2/45 + 1/36 = 244/495
Sest 244/495 on täpselt 49,3%. See on veidi alla 50%. Tegelikult ei leia sa tõenäoliselt paremat võimalust võita 1:1 väljamakseid. Välja arvatud võib-olla blackjack, kui oskate kaarte lugeda.
Blackjacki tõenäosus
Blackjack on õnnemäng, kus tõenäosus on kõige olulisem. Blackjackis saate oma oskuste ja teadmistega mõjutada maja serva. Sa pead selleks lihtsalt teadma optimaalset strateegiat ja kui sa oskad kaarte loendada, siis mängid isegi mängija eelisega. Ümberringi ei ole teil tegelikult vaja teada kõiki konkreetseid tõenäosusi, sest kõik need arvutused on juba teinud matemaatikud enne teid, kes mõtlesid välja kõik blackjacki taktikad ja strateegiad.
Kuid huvi pärast näitame, kuidas arvutada tõenäosust mõnede oluliste nähtuste puhul blackjackis.
Kui me vaatame tõenäosuse probleemi kaardipaki perspektiivist, siis on selge, et võimalike tulemuste arv kasvab kiiresti. Blackjacki mängitakse 52 kaardist koosneva kaardipakiga, millel on 4 värvi ja 13 väärtust. See annab järgmised koefitsiendid:
- Tõmban pakist ässa (või ükskõik millise üksiku kaardi): 4/52=0,0769 (7,69%)
- Tõmban kaardipaki: 13/52=0,25 (25%)
Kuid erinevalt näiteks mündiviskest, ruletist või mänguautomaadist on kaardipakil midagi "mälu". Või õigemini tähendab see, et eelmised tulemused mõjutavad praeguseid ja tulevasi käike. Selle põhjuseks on asjaolu, et kaardipakist on maha võetud kaart ja see muudab lähteolukorda. Vaatleme näidet, kus esimene 52-kaardilisest kaardipakist tõmmatud kaart on äss (7,69% tõenäosus). Tõenäosus, et äss tõmmatakse uuesti teise kaardina kaardipakist, on nüüd erinev. Pärast esimest loosimist on ässade arv langenud 3-le ja kaartide arv 51-le.
Tõenäosus blackjack natural
See, mis iga mängijat kõigepealt huvitab, on blackjacki tõenäosus. See tähendab, kui suur on tõenäosus, et mängija saab kohe vooru alguses ässa ja kümne kaardi - teisisõnu, naturaalkaardi.
See olukord võib tekkida kahel viisil ja kui me liidame need kaks võimalust, saame blackjacki tõenäosuse:
📌 Märkus: Me loeme ühe teki blackjack'i puhul. Seega 52 kaarti, 4 ässa ja 16 kümnist. Diileri kaart ei ole nähtav, seega ei mõjuta see tõenäosust.
- Mängija saab esimese ässa ja kümne kaardi.
Mängijale jagatakse esimene äss kaart tõenäosusega 4/52. Seega peab mängija saama teise kaardi kümnega ja selle tõenäosus on 16/51. Need kaks tõenäosust tuleb omavahel korrutada, et saada 16/663.
- Mängija saab esimese kümne kaardi ja ässa.
Tõenäosus, et mängija saab esimese kaardi väärtusega 10, on 16/52. Mängija tõenäosus, et ta saab pärast seda ässa, on 4/51. Pärast korrutamist saame 16/663.
Kui me tahame teada blackjacki saamise tõenäosust, siis liidame need kaks nähtust lihtsalt kokku. Seega 16/663 + 16/663 = 32/663 = 4,827%. Teisisõnu, mängija saab blackjacki umbes iga 20 käe järel. Mitmepakkide tabelite tõenäosust saab arvutada sarnaselt, mida me juba tegime teie jaoks.
|
Pakettide arv |
Tõenäosus |
|
1 |
4,827 % |
|
2 |
4,780 % |
|
3 |
4,764 % |
|
4 |
4,757 % |
|
5 |
4,752 % |
|
6 |
4,749 % |
Tõenäosus, et see läheb katki
Samuti võib olla huvitav teada, millised on teie tõenäosus, et te ei saa seda teha. Jällegi keskendume näidissituatsioonile, kus mängite ühe teki lauas ainult diileriga. Vaatleme väga lihtsat olukorda, kus mängijal on 2 kaarti väärtusega kokku 10, nii et tal on 20 punkti. Olukorras, kus mängija saab kolmanda kaardi, on pakist juba 3 kaarti välja mängitud. Nii jääb pakki 49 kaarti. Nendest 49 kaardist aitab teid ainult 4 ässa. Neist 49-st on 45 kaarti soovimatu. Seega on tabamuse tõenäosus 45/49=0,9183673.
Sarnaselt saab arvutada ka teisi tõenäosusi. Te peate alati suutma olukorda õigesti ette kujutada. See on kõik.
|
Käe väärtus |
Rikkumiste tõenäosus |
|
21 |
100 % |
|
20 |
92 % |
|
19 |
85 % |
|
18 |
77 % |
|
17 |
69 % |
|
16 |
62 % |
|
15 |
58 % |
|
14 |
56 % |
|
13 |
39 % |
|
12 |
31 % |
|
11 vähem |
0 % |
Vaatame järgmisena, kui tõenäoline on, et diiler teeb iga kaardi puhul basti.
|
Käe väärtus |
Rikkumiste tõenäosus |
|
2 |
35,30 % |
|
3 |
37,56 % |
|
4 |
40,28 % |
|
5 |
42,89 % |
|
6 |
42,08 % |
|
7 |
25,99 % |
|
8 |
23,86 % |
|
9 |
23,34 % |
|
10, J, Q, K |
21,43 % |
|
Ace |
11,65 % |
Pokeri tõenäosus
Pokker on veel üks kaardimäng, kus tõenäosus on äärmiselt oluline. Muu hulgas. Nii et vaatame, millised on teie võimalused pokkeris.
Pre-flop tõenäosus
Nüüd, kui me oleme kirjeldanud, kuidas tõenäosus kaardipaki puhul toimib, läheme praktiliste rakenduste juurde. Kõigepealt näitame, kuidas arvutada tõenäosust, et käes on paarid otsas. (näiteks palju räägitud ässad). Sellisel juhul tuleb tõenäosused omavahel korrutada.
(4/52) x (3/51) = (12/2652) = (1/221) = 0,004524 (0,45 %)
📌 Märkus: Kui mängid pokkerit kasiinos, kus jagatakse umbes 30 kätt tunnis, saad ässapaari umbes kord iga 7 ja poole tunni jooksul.
Millised on siis võimalused saada mõni 13 võimalikust paarist, kui te jagate? Võime eeldada, et tõenäosus on 1/221 iga üksikpaari kohta (vt valemit eespool). Neid paare võib olla kokku 13, seega on arvutamise valem 13/221=0,0588. Seega võib oodata paari umbes iga 35 mängu järel.
Tõenäosus pokkeris mängija vastu mängija
Kuid pokker on mitme mängijaga mäng, mida tavaliselt mängitakse üksteise vastu. Nii et siin on valik kõige tavalisemaid pre-flop olukordi.
|
Sinu käsi |
Teie vastase käsi |
Võidutõenäosus |
|
Kõrge paar |
Kaks madalat kaarti |
83 % |
|
Kõrge paar |
Madal paar |
82 % |
|
Keskmine paar |
Kõrge, madal kaart |
71 % |
|
Kaks kõrget kaarti |
Kaks madalat kaarti |
63 % |
|
Kaks kõrget kaarti |
Madal paar |
55 % |
Tõenäosuse arvutamine "outide" järgi
Kui teil õnnestub flopil kaarte näha, siis huvitab teid kindlasti veelgi enam, millised on teie võimalused oma käe parandamiseks. Antud juhul räägime nn "outidest". Pokkeri puhul viitab see termin mis tahes kaartidele, mis võivad sind aidata. Selline tavaline juhtum võib olla, kui mängijal on kaks ühe värvi kaarti ja flopis ilmub veel kaks sama värvi kaarti. Mängijal on siis 4 kaarti, et teha flush ja seega on tal 9 outi, mis jätab 9 kaarti, millega moodustada flush.
|
Väljalangemiste arv |
Flop - Turn |
Turn - jõgi |
Pöörake jõge |
|
20 |
42,6 % |
43,5 % |
67,5 % |
|
19 |
40,4 % |
41,3 % |
65,0 % |
|
18 |
38,3 % |
39,1 % |
62,4 % |
|
17 |
36,2 % |
37,0 % |
59,8 % |
|
16 |
34,0 % |
34,8 % |
57,0 % |
|
15 |
31,9 % |
32,6 % |
54,1 % |
|
14 |
29,8 % |
30,4 % |
51,2 % |
|
13 |
27,7 % |
28,3 % |
48,1 % |
|
12 |
25,5 % |
26,1 % |
45,0 % |
|
11 |
23,4 % |
23,9 % |
41,7 % |
|
10 |
21,3 % |
21,7 % |
38,4 % |
|
9 |
19,1 % |
19,6 % |
35,0 % |
|
8 |
17,0 % |
17,4 % |
31,5 % |
|
7 |
14,9 % |
15,2 % |
27,8 % |
|
6 |
12,8 % |
13,0 % |
24,1 % |
|
5 |
10,6 % |
10,9 % |
20,3 % |
|
4 |
8,5 % |
8,7 % |
16,5 % |
|
3 |
6,4 % |
6,5 % |
12,5 % |
|
2 |
4,3 % |
4,3 % |
8,4 % |
|
1 |
2,1 % |
2,2 % |
4,3 % |
📌 Märkus: Outide tõenäosuse arvutamiseks on olemas väga lihtne meetod, nii et seda saab teha otse laua taga. Seda nimetatakse üldiselt "nelja ja kahe" reegliks. Pärast floppi korrutab mängija lihtsalt outide arvu neljaga, et leida turni ja riveri tõenäosus. Kui ta ei saa kaarti turnil, korrutab ta lihtsalt väljalangevuste arvu kahega, et saada ligikaudne tõenäosus, et ta saab kaardi riveril.
Jällegi võime kasutada näidet, kus pärast floppi on 4 sama värvi kaarti. Seega on sinu väljapääsud 9 kaarti ja värvitulemuse tõenäosus pärast turni ja riveri on 36% (9x4). Oletame, et sa ei saa kaarti oma käigul. Sellisel juhul korrutame väljaminekud kahega ja leiame, et meil on 18% (9x2) tõenäosus, et riveril on selle värvi kaardid otsas. Nagu tabelit võrreldes näete, on see meetod tõesti lihtne, kuid teisest küljest ebatäpne, kuid seda saab kasutada.

 ET
ET  English
English  čeština
čeština  Polski
Polski  Slovenčina
Slovenčina  Русский
Русский  Deutsch
Deutsch  Slovenski
Slovenski  Dutch
Dutch  Svenska
Svenska  Português
Português  Italiano
Italiano  Español
Español  Français
Français  Suomalainen
Suomalainen  Български
Български  Românesc
Românesc  Magyar
Magyar  Ελληνική
Ελληνική  Latviešu
Latviešu  Lietuvių
Lietuvių  やまと
やまと  中国
中国  Dansk
Dansk  Türkçe
Türkçe  ID
ID  Українська
Українська  한국어
한국어  Norsk
Norsk 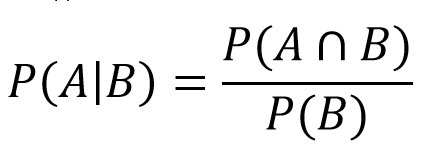


Kommentaaride lisamiseks peate olema sisse logitud.